ГЛАВА 8. ДИФРАКЦИЯ Плоской электромагнитной волны на круглом ОТВЕРСТИи в идеально проводящем экране и на идеально проводящем диске

8.1 Дифракция плоской электромагнитной волны на круглом отверстии в идеально проводящем экране

Так как свет представляет собой электромагнитную волну, рассмотрим схему наблюдения дифракции от круглого отверстия на примере световой волны (рис.8.1). Пусть 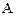– точечный источник света, 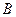– непрозрачный экран с круглым отверстием 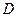с центром в точке 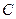, – экран, на котором наблюдается дифракционная картина.

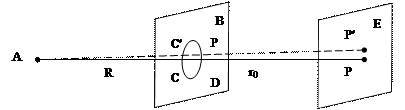Рис. 8.1 - Схема наблюдения дифракции от круглого отверстия

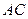В случае прямолинейного распространения света мы получили бы на экране освещенный круг с резкими краями. В действительности картина более сложная. Результат действия волнового фронта, проходящего через отверстие , в точке , лежащей на оси , мы уже определили. Освещенность в точке больше или меньше освещенности от незакрытого фронта в зависимости от того, уложится ли при данных условиях опыта на площади отверстия 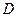нечетное или четное число зон Френеля. Для определения освещенности в какой-либо точке 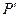, не лежащей на оси 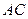, мы можем рассуждать следующим образом. Если бы экрана 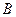не существовало вовсе, то мы определили бы действие волнового фронта в точке 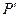, построив кольцевые зоны Френеля, центром для которых служила бы точка 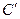. При наличии экрана 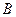отверстие 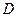расположится не концентрически по отношению к этим зонам. Открытая часть зон будет выглядеть, как это изображено на рис.8.2, где нечетные зоны заштрихованы.

Действие этих зон в точке 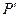определятся не только их числом, но и тем, какая часть каждой из зон открыта.

Рис. 8.2 – Зоны Френеля

Точный подсчет амплитуды суммарного колебания в точке 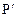сложный, но ясно, что при удалении от точки мы периодически встретим места с большей или меньшей освещенностью. Так как вся картина должна обладать круговой симметрией, то около точки возникнут чередующиеся более светлые и менее светлые кольца. Число наблюдаемых светлых и темных колец и их положение зависят от числа зон, умещающихся на площади отверстия 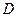при данных условиях наблюдения. Число зон 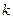, укладываемое на отверстии радиуса 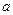определяется равенством:

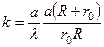, (8.1)

где - расстояние от источника до экрана; 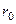- расстояние от экрана до зоны наблюдения.

Как видно, это число 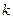зависит от отношения радиуса отверстия 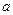к длине волны 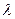и от расстояний и 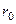. При увеличении расстояния формула (8.1) приобретает вид:

или ,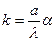

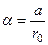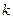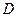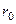где - угол, под которым видно отверстие в экране из точки . Число зон может быть мало и при значительных размерах отверстия , если только расстояния и достаточно велики.

Если на площади отверстия укладывается лишь одна центральная зона Френеля или часть ее, то на экране 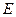получается размытое пятно, не окруженное светлыми и темными кольцами. Если на площади отверстия укладывается большое число зон Френеля, то освещенность вблизи точки получается практически равномерной и лишь у краев геометрической тени наблюдается чередование весьма узких светлых и темных полос.

Все рассуждения касаются точечного источника света 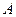. Всякий же реальный источник протяжен. В этом случае источник 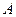мысленно разбивается на точечные источники, каждый из которых даст свою дифракционную картину. Эти дифракционные картины будут несколько смещены друг относительно друга. Размеры источника должны быть настолько малы, чтобы темные и светлые полосы, даваемые отдельными точками источника, не перекрывались, что привело бы к полному размыванию картины.

В случае круглого отверстия общий вид ДН такой же, как и при прямоугольном отверстии, а угловая ширина луча определяется

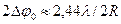. (8.2)

Схема наблюдения дифракции в радиодиапазоне приведена на рис.8.3.

Рис. 8.3 – Схема наблюдения дифракции

Установка состоит из генератора 3-х сантиметрового диапазона, рупорного излучателя, экрана с отверстиями, приемной антенны-рупора и измерительного усилителя. Размеры отверстий изменяются. Изменение отверстий влечет за собой изменение амплитуды поля в точке приема, которая фиксируется измерительным прибором.

При размерах экрана порядка 75-80 см и достаточно узкой диаграмме направленности рупорного излучателя на передающем конце можно пренебречь влияниями отражений от поверхности стола, на котором смонтирована установка.

8.2 Дифракция плоской электромагнитной волны на идеально проводящем диске

Рассмотрим схему наблюдения дифракции от непрозрачного диска. Пусть излучение из точки источника 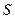(рис.8.4) падает на диск радиусом , за которым на прямой, перпендикулярной плоскости диска и проведенной через его центр, располагается точка наблюдения . Будем считать, что размер диска во много раз меньше расстояний a от диска до источника и от диска до точки наблюдения .

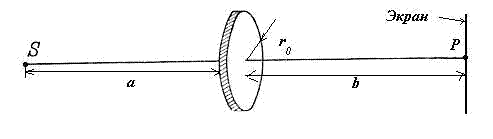
Рис. 8.4 - Схема наблюдения дифракции от непрозрачного диска

Предположим, что диск в точке наблюдения 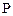«закрывает» 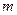зон Френеля. Тогда амплитуда излучения 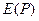в точке наблюдения будет равна алгебраической сумме амплитуд волн открытых зон Френеля:

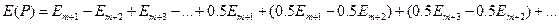
Учитывая, что амплитуды соседних зон Френеля примерно равны друг другу, однотипные выражение в скобках можно положить равными нулю, получим

.

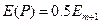Отсюда следует, что в центре дифракционной картины, создаваемой диском, всегда наблюдается пятно максимума интенсивности, независимо от размеров диска (рис.8.5). В истории физики это свойство зон Френеля явилось доказательством волновой природы света.

Рис. 8.5 – Дифракционная картина от непрозрачного диска

Дифракционная картина от диска, наблюдаемая на экране (рис.8.5), имеет характер чередующихся колец минимумов и максимумов интенсивности, в центре которых находится пятно максимума. Структура дифракционной картины электромагнитной волны от непрозрачного диска имеет общие черты с дифракционной картиной света от отверстия того же диаметра в непрозрачном экране в соответствии с принципом Бабине.

Пусть для определённости диск закрывает только одну зону Френеля. Тогда в соответствии с принципом Бабине в центре дифракционной картины диска амплитуда волны определяется разностью амплитуд волны источника в отсутствие экрана, и волны от отверстия, имеющего размер первой зоны Френеля. Учитывая, что амплитуда волны от первой зоны Френеля в два раза больше, чем амплитуда волны источника в точке наблюдения, получаем, что интенсивность волны за диском равна интенсивности волны источника в отсутствии диска.

Если же диск закрывает две зоны Френеля, то в соответствии с принципом Бабине в центре дифракционной картины диска амплитуда волны определяется амплитудой волны источника в отсутствие экрана, поскольку амплитуду волны, создаваемой отверстием того же диаметра, что и диск, приближённо можно полагать равной нулю. Проведенные рассуждения справедливы для диска, открывающего произвольное не очень большое число чётных или нечётных зон Френеля.

Таким образом, амплитуда волны в центре дифракционной картины от диска любого размера равна половине амплитуды волны от первой открытой зоны Френеля, что совпадает с результатом проведенных выше расчётов. На периферии дифракционной картины от диска распределение интенсивности в основном определяется амплитудой волны источника, на которую «накладываются» затухающие по мере удаления от центра картины колебания волн от частично открытых зон Френеля отверстием в непрозрачном экране того же диаметра, что и рассматриваемый диск.

Если размер диска во много раз меньше первой зоны Френеля, то диск как бы не «отбрасывает» тени. Если размер диска закрывает много зон Френеля, в центре дифракционной картины пятна максимума практически не видно т.к. 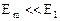, регистрация излучения в области геометрической тени практически дает ноль, а дифракционные кольца наблюдаются в узкой области.

Радиус первой зоны Френеля . Аналогично для n -ной зоны 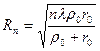, тогда как площади всех зон равны: .

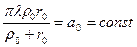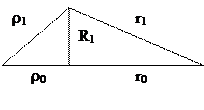Рис. 8.6 - К расчету радиусов зон Френеля
ГЛАВА 9. Дифракция плоской электромагнитной волны на идеально проводящем металлическом шаре

Поиск по сайту: