 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Интегральные характеристики дифракции
Процесс дифракции характеризуют при помощи интегральных энергетических параметров, таких как: поперечное сечение рассеяния и поперечное сечение прохождения.
Дифракция на теле ограниченного размера описывается при помощи поперечного сечения рассеяния  :
:
 . (1.8)
. (1.8)
Этот параметр определяется как отношение полного потока энергии рассеяния 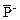 к абсолютному значению вектора Пойтинга
к абсолютному значению вектора Пойтинга 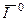 (падающей волны),
(падающей волны), 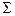 - какая-либо поверхность, охватывающая объект дифракции (рис.1.1, а).
- какая-либо поверхность, охватывающая объект дифракции (рис.1.1, а).
Например, плоская однородная электромагнитная волна падает на металлический лист (поверхность 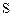 ), размеры которой велики по сравнению с длиной волны
), размеры которой велики по сравнению с длиной волны 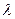 (рис.1.1, б). Будем считать его идеально проводящим. В приближении геометрической оптики вычислим поток энергии волны, отраженной от листа:
(рис.1.1, б). Будем считать его идеально проводящим. В приближении геометрической оптики вычислим поток энергии волны, отраженной от листа:
 . (1.9)
. (1.9)

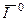
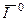
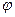

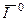

V  S
S 
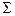
a) б) в)
Рис. 1.1 – Дифракция на объектах различной формы
Однако, это еще не полный поток энергии рассеяния: существование области тени следует рассматривать как результат наложения на падающую волну 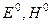 локализованного в этой области поля
локализованного в этой области поля  (в результате чего полное поле уничтожается). Следовательно, полный поток энергии рассеяния вдвое больше, чем
(в результате чего полное поле уничтожается). Следовательно, полный поток энергии рассеяния вдвое больше, чем  . Поперечное сечение рассеяния в приближении геометрической оптики
. Поперечное сечение рассеяния в приближении геометрической оптики
 . (1.10)
. (1.10)
Максимальное значение этой величины вдвое превышает площадь листа (случай нормального падения).
Рассматривая дифракцию на отверстии (рис.1.1, в), вводят понятие поперечного сечения прохождения
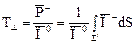 , (1.11)
, (1.11)
где незамкнутая поверхность  построена так, что через нее проходит весь поток энергии рассеяния. В приближении геометрической оптики поперечное сечение прохождения равно площади отверстия:
построена так, что через нее проходит весь поток энергии рассеяния. В приближении геометрической оптики поперечное сечение прохождения равно площади отверстия: 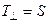 .
.
Поиск по сайту: