Дифракция плоской электромагнитной волны на щели в идеально проводящем экране

Рис. 3.1 – Дифракция плоской волны на щели в идеально проводящем экране

Поляризация падающей волны такова, что комплексная амплитуда вектора напряженности электрического поля имеет вид

.

Падающая волна перемещается слева направо, существуя в полупространстве . Требуется определить дифрагированное электромагнитное поле в полупространстве за препятствием. Электромагнитное поле в однородной среде без источников является соленоидальным, т.е.

, ,

и подчиняется векторным уравнениям Гельмгольца

(3.1)

Из физических соображений ясно, что на достаточно большом удалении от возбуждающей щели силовые линии электрического вектора в полупространстве по форме будут напоминать дуги окружностей с центрами в точке . Поэтому у вектора имеются две отличные от нуля проекции и , а третья возможная проекция заведомо отсутствует. Однако, если интересоваться волновым процессом лишь в области пространства вблизи оси , то можно предположить, что поляризационная структура дифрагированного поля такая же, как и у падающей волны. Поэтому, приближенно, в указанной области пространства электрический вектор будет иметь единственную отличную от нуля проекцию . Такое предположение сводит векторную задачу к скалярной, что существенно упрощает выкладки.

Итак, нам нужно найти решение скалярного уравнения Гельмгольца

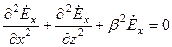(3.2)

в полупространстве , удовлетворяющее определенным граничным условиям на плоскости . В соответствии с принципом физической оптики потребуем, чтобы значение поля обращалось в нуль на участках поверхности закрытых идеальным проводником, а в щели равнялось невозмущенной напряженности падающего поля .

Граничные условия для этого случая таковы:

(3.3)

Применим к уравнению метод разделения переменных и будем решать его в виде . Частным решением уравнения Гельмгольца (3.2), имеющим вид произведения двух функций, является

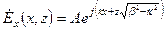(3.4)

при любых значениях амплитудного коэффициента 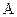и параметра 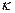. Выбирая этот параметр тем или иным образом можно описывать любые волновые процессы.

1. Если значение действительно и , то решение (3.4) описывает однородную плоскую волну с постоянной амплитудой, распространяющуюся под углом к оси , который зависит от соотношения между и .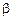

2. При , выражение (3.4) описывает неоднородную плоскую волну, распространяющуюся вдоль оси со скоростью, меньшей скорости света и амплитуда волны экспоненциально убывает с ростом координаты .

Из частных решений (3.4) можно построить общий интеграл:

(3.5)

с неизвестной пока весовой функцией , которую нужно подобрать так, чтобы удовлетворить граничным условиям (3.3). Подставив в (3.5) значение , получим

(3.6)

Видно, что – преобразование Фурье от распределения поля в плоскости экрана. Чтобы найти эту функцию, следует обратить формулу (3.6) по Фурье:

. (3.7)

В нашем случае .

Таким образом, получено интегральное представление волнового поля в полупространстве за экраном:

. (3.8)

Вычислим данный интеграл методом стационарной фазы. Введем полярную систему координат: , . Тогда

. (3.9)

Точка стационарной фазы служит корнем уравнения:

, (3.10)

откуда

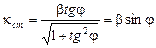. (3.11)

Ограничимся наиболее важным случаем малоугловой дифракции, когда поле вычисляется в непосредственной близости от оси и поэтому . Выполнив предельный переход в соответствии с (3.11) убеждаемся, что при сделанном предположении точка стационарной фазы приближенно имеет координату .

Вторая производная от показателя экспоненциальной функции, входящей в подынтегральное выражение формулы (3.8) равна

.

Используя формулу

, (3.12)

окончательно получим

. (3.13)

Данное выражение описывает цилиндрическую волну, которая уже не является однородной, а имеет угловую зависимость амплитуды поля, выраженную тем сильнее, чем больше безразмерный параметр , т.е. чем больше отношение ширины щели к длине волны. Интенсивность излучения щели максимальна в направлении ; первый дифракционный нуль излучения наблюдается под углами , которые удовлетворяют равенствам .

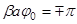Угловая зависимость дифракционного поля щели имеет лепестковый характер (рис.3.2). В направлении формируется основной лепесток, по обе стороны от которого возникают симметричные боковые лепестки рассеянного поля, т.к. токи, обусловленные падающей волной, затекают за кромки щели.

Рис. 3.2 – Диаграмма направленности дифракционного поля за щелью в идеально проводящем экране

Поиск по сайту: