АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Уравнение эйконала

Читайте также:
  1. E) Для фиксированного предложения денег количественное уравнение отражает прямую взаимосвязь между уровнем цен Р и выпуском продукции Y.
  2. IV. УРАВНЕНИЕ ГАМЛЕТА
  3. V2: Волны. Уравнение волны
  4. V2: Уравнение Шредингера
  5. Адиабатический процесс. Уравнение адиабаты (Пуассона). Коэффициент Пуассона.
  6. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  7. В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени
  8. В простом случае обычное дифференциальное уравнение имеет вид
  9. В этом случае уравнение Эйлера принимает вид
  10. Влияние температуры на константу равновесия. Уравнение изобары
  11. Внутреннее трение (вязкость) жидкости. Уравнение Ньютона
  12. Волна вероятности. Уравнение Шредингера

Определим функцию . Подставим (6.2) в (6.1), учтя, что . По правилам вычисления производной от сложной функции находим

. (6.3)

Как известно из векторного анализа,

,

где 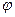- скалярное поле и 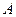- векторное поле – произвольные гладкие функции координат. Получим

. (6.4)

Подставим (6.4) в (6.1), находим

. (6.5)

Учтем, что в рамках метода геометрической оптики и поэтому коэффициент фазы 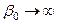. Следовательно, можно пренебречь вторым слагаемым в левой части уравнения (6.5). После сокращения на общий множитель приходим к эквивалентному уравнению

, (6.6)

или в развернутом виде

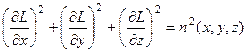. (6.7)

Данное нелинейное дифференциальное уравнение в частных производных первого порядка называется уравнением эйконала. Это уравнение является основным соотношением геометрической оптики пространственно неоднородной среды.

Отметим следующие важные факты:

- в уравнение эйконала не входит длина волны, поэтому метод геометрической оптики не учитывает дифракционных и интерференционных эффектов;

- метод геометрической оптики справедлив, когда во всех точках пространства.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)