Поле на бесконечно больших расстояния от нити с электрическим током

В качестве примера расчета интерференции волн рассмотрим задачу об электромагнитном поле, которое создается бесконечно тонкой нитью электрического тока, ориентированной вдоль оси цилиндрической системы координат (рис.2.1).

Ток изменяется во времени по гармоническому закону с частотой ; комплексная амплитуда тока в каждой точке оси считается неизменной.

Электродинамические свойства среды заданы параметрами и .

Рис. 2.1 – Вычисление поля на больших расстояниях от нити тока

Бесконечно большое расстояние реализуется для случая, когда от точки наблюдения достаточно велико в волновом масштабе, т.е. . Если мысленно разбить излучающую нить на бесконечно малые отрезки длиной , то каждый из них будет представлять собой элементарный электрический излучатель (диполь).

Пусть - текущая координата вдоль нити тока, а точка наблюдения лежит в плоскости . Длина отрезка, соединяющего выделенный элемент тока и точку наблюдения, .

Азимутальная координата 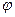в цилиндрической системе координат и в локальной сферической системе, связанной с излучающим элементом тока оказывается одной и той же. Поэтому бесконечно малый вклад в комплексную амплитуду магнитного вектора можно определить, воспользовавшись формулой:

,

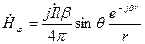получим

. (2.1)

Из рисунка 2.1 можно определить 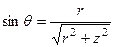. На основании принципа суперпозиции комплексная амплитуда напряженности результирующего магнитного поля определяется как:

(2.2)

Выражения, подобные (2.2), называются интерференционными интегралами и часто встречаются в теории дифракции волн. Сложность вычисления таких интегралов состоит в том, что мнимый показатель экспоненты под знаком интеграла содержит безразмерный «большой» параметр . Поэтому действительная и мнимая части этой функции быстро осциллируют с изменением переменной и вклады обеих частей в интеграл оказываются знакопеременными.

Поиск по сайту: