 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Дифракция плоской электромагнитной волны на идеально проводящем металлическом шаре
Для решения задачи дифракции плоской волны на шаре (рис.9.3) внутреннее 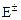 и внешнее
и внешнее  поля дифракции разлагаются в ряды с неопределенными коэффициентами, которые определяются при наложении граничных условий. При этом используются сферические гармоники и на основе скалярных решений уравнения Гельмгольца строятся соответствующие векторные решения уравнений Максвелла.
поля дифракции разлагаются в ряды с неопределенными коэффициентами, которые определяются при наложении граничных условий. При этом используются сферические гармоники и на основе скалярных решений уравнения Гельмгольца строятся соответствующие векторные решения уравнений Максвелла.
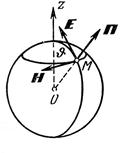
Рис. 9.3 – Дифракция электромагнитной волны на идеально проводящем металлическом шаре
Задавая падающую волну (рис.9.3) в форме
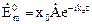 ,
,  , (9.5)
, (9.5)
где 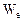 - энергия электромагнитного поля. Нас будет интересовать внешнее поле дифракции
- энергия электромагнитного поля. Нас будет интересовать внешнее поле дифракции 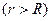
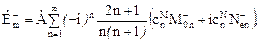
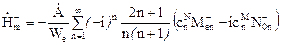 . (9.6)
. (9.6)
В этих формулах
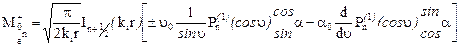 ;
;
 (9.7)
(9.7)
где 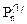 - присоединенные функции Лежандра; индекс
- присоединенные функции Лежандра; индекс 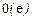 означает выбор верхнего (нижнего) варианта тригонометрической функции и знака. Функции
означает выбор верхнего (нижнего) варианта тригонометрической функции и знака. Функции  и
и 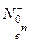 - получаются из
- получаются из 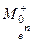 и
и 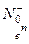 путем замены
путем замены 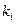 на
на 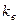 и
и 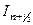 на
на 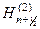 . Неопределенные коэффициенты
. Неопределенные коэффициенты 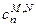 и
и 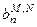 выражаются следующим образом:
выражаются следующим образом:
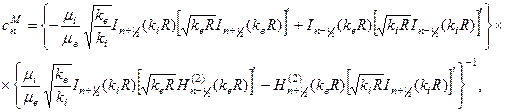
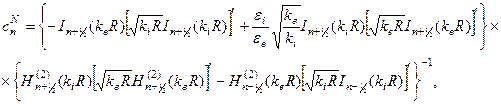 (9.8)
(9.8)
и 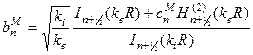 ,
,
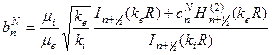 . (9.9)
. (9.9)
На рис.9.4 представлены некоторые результаты численного моделирования поля дифракции в случае идеально проводящего шара (в предыдущих формулах 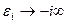 ), расположенного в вакууме:
), расположенного в вакууме: 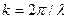 .
.
Показанные графически угловые зависимости  и
и 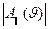 соответствуют следующему выражению поля дифракции в дальней зоне:
соответствуют следующему выражению поля дифракции в дальней зоне:
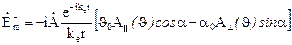 ,
,
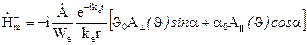 . (9.10)
. (9.10)
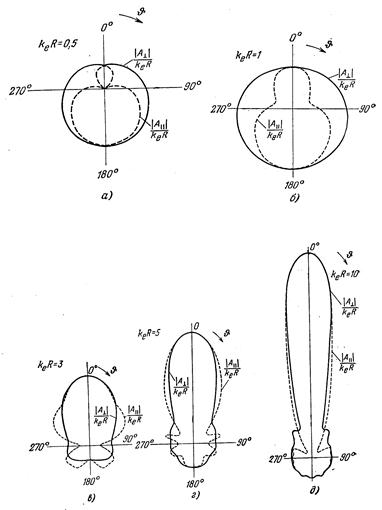
Рис. 9.4 – Угловое распределение интенсивности
Как и в случае идеально проводящего цилиндра, с ростом относительного радиуса объекта наблюдается обострение максимума рассеянного излучения в области геометрической тени.
Поиск по сайту: