 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Уравнение лучей
Чтобы описать волновой процесс в приближении геометрической оптики, достаточно располагать семейством поверхностей постоянных фаз
,
которое образовано решениями уравнения эйконала (6.7).
Рассмотрим лучевую картину поля (рис.6.1).
2
Рис. 6.1 – Лучевая картина поля: 1 – волновые фронты; 2 – лучи
Лучи образуют семейство линий, ортогональных к волновым фронтам. Вектор, касательный к лучу в некоторой точке пространства, указывает направление перемещения волнового фронта локально-плоской волны. Отсюда следует, что касательная к лучу ориентирована вдоль вектора 
, указывающего направление быстрейшего изменения эйконала в пространстве.
Рассмотрим какой-нибудь конкретный луч. Пусть 
- радиус-вектор выбранной точки на луче, 
- длина кривой, отсчитываемая вдоль луча в одном из двух возможных направлений.
Исходя из уравнения эйконала, запишем единичный вектор 
(лучевой орт) в некоторой произвольной точке:
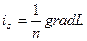. (6.9)
В прямоугольной декартовой системе координат этот единичный вектор имеет направляющие косинусы 
, 
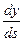и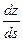 
, т.е. имеет место разложение вида
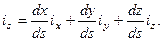(6.10)
Приравнивая (6.9) и (6.10), получим дифференциальное уравнение лучей:
, (6.11)
правая часть уравнения содержит эйконал 
. Однако, уравнение можно преобразовать таким образом, чтобы в правую часть уравнения (6.11) входило только пространственное распределение показателя преломления 
, известное заранее. Получаем уравнение лучей
, (6.12)
которое эквивалентно системе трех дифференциальных уравнений в координатной записи:
, 
, 
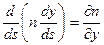. (6.13)
Уравнения (6.12) и (6.13) дают возможность решить основную задачу геометрической оптики – построить лучевые траектории.
Таким образом, создав в одной точке пространства плоскую волну с заданным направлением лучевого вектора, мы получаем в другой точке пространства также плоскую волну, у которой направление распространения будет другое. Построив один луч, мы не получим сведений об амплитудах волн на входе и выходе.
Простейший случай – распространение плоских волн в однородной среде, когда лучи представляют собой прямые линии.
Поиск по сайту: