Метод стационарной фазы

Методом стационарной фазы пользуются для приближенной оценки интерференционных интегралов.

Суть этого метода состоит в том, что в интеграл основной вклад вносит лишь малый участок оси вокруг так называемой точки стационарной фазы, в которой производная от фазовой функции обращается в нуль. Вклады от остальных участков оси взаимно компенсируются из-за знакопеременного характера подынтегрального выражения.

Рассмотрим интеграл

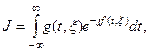(2.3)

где - медленная функция формальной переменной , - большой параметр задачи. Пусть - единственный действительный корень уравнения (это рассуждение справедливо на случай нескольких корней). Тогда вблизи этой точки можно функцию разложить в ряд Тейлора

. (2.4)

Разложение (2.4) представляет собой квадратичную функцию аргумента .

Подставляя (2.4) в (2.3) приходим к приближенному равенству

. (2.5)

Имеются табличные интегралы, справедливые при любых значениях .

.

Тогда, представив экспоненциальную функцию в подынтегральном выражении из (2.5) как сумму действительной и мнимой частей, получим приближенно

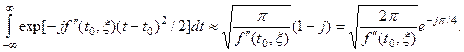(2.6)

Подставив (2.6) в (2.5) и считая , находим

. (2.7)

Применим метод стационарной фазы к оценке интерференционного интеграла (2.2). Здесь поэтому точка стационарной фазы имеет координату . Вычислив вторую производную, находим, что . Следовательно,

откуда получаем комплексную амплитуду единственной отличной от нуля проекции магнитного вектора:

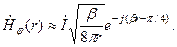(2.8)

Чтобы определить вектор напряженности электрического поля, следует воспользоваться первым уравнением Максвелла . Учтем, что в данном случае в силу геометрических особенностей задачи. Кроме того, . Тогда

, (2.9)

откуда следует, что во всем пространстве электрический вектор имеет единственную отличную от нуля проекцию вдоль оси с комплексной амплитудой

.

Для описания поля на расстояниях от возбуждающей нити, значительно превышающих длину волны, т.е. при значениях , первым слагаемым в квадратных скобках можно пренебречь по сравнению со вторым и получить

. (2.10)

Формулы (2.8) и (2.10) описывают однородную цилиндрическую волну. Поверхности равных фаз такой волны представляют собой концентрические цилиндры, перемещающиеся в радиальном направлении с фазовой скоростью . Для рассматриваемой задачи специфичен дополнительный фазовый сдвиг на между возбуждающим током и напряженностью поля.

На большом удалении от нити тока цилиндрическая волна является локально-плоской. Действительно, здесь . Легко убедиться в том, что вектор ориентирован в радиальном направлении. Интересно отметить также, что амплитуды векторов и в цилиндрической волне уменьшаются с ростом радиуса не по закону , как в сферической волне, а пропорционально множителю , т.е. значительно медленнее.

Строгое решение задачи о возбуждении свободного пространства нитью синфазного тока приводит к следующему результату:

, (2.11)

где - функция Ганкеля второго рода 1-го порядка, которая при больших значениях аргумента имеет следующее асимптотическое представление:

. (2.12)

Подставив это выражение в (2.11), сразу приходим к формуле (2.8).

Поиск по сайту: