АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Теорема эквивалентности

Читайте также:
  1. I. 4.1. Первая теорема двойственности
  2. S-M-N-теорема, приклади її використання
  3. Б1 1.Системы линейных алгебраических уравнений (СЛУ). Теорема Кроникера-Капелли. Общее решение СЛУ.
  4. Базисный минор и ранг матрицы. Теорема о базисном миноре
  5. Билет 22Понятие евклидова пространства, неравенство Коши-Буняковского. Теорема Кронекера Капелли.
  6. Билет 5 Теорема Безу и следствия из неё. Основная теорема алгебры.
  7. Внешние эффекты (экстерналии). Теорема Коуза.
  8. Внешние эффекты и внешние затраты. Государственная политика в случаях их возникновения. Теорема Коуза.
  9. Внешние эффекты трансакционные издержки. Теорема Коуза
  10. Внешние эффекты, их виды и последствия. Теорема Коуза
  11. Внешние эффекты. Теорема Коуза.
  12. Внешние эффекты. Теорема Коуза.

Предположим, что имеется произвольный объем с гладкой замкнутой поверхностью 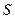. Внутри объема некоторым образом распределены возбуждающие источники, характеризуемые объемными плотностями сторонних электрических 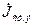и магнитных токов. Кроме того, будем считать, что на поверхности 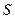заданы касательные составляющие векторов искомого поля, возникающего под действием источников внутри объема и внешних источников.

Вычислим векторы электромагнитного поля во всех внутренних точках объема . Рассмотрим в объеме две системы векторов. Одна из них - отображает искомое поле. Другая 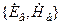- отображает совокупность векторов вспомогательного поля, которое создается воображаемым элементарным электрическим излучателем внутри объема . Будем считать, что ось излучателя ориентирована вдоль единичного вектора . Предположим, что амплитуда тока в излучателе и его длина таковы, что . Тогда соответствующая плотность тока имеет комплексную амплитуду

где 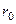- радиус-вектор точки относительно произвольно выбираемой точки начала координат.

Обратимся к лемме Лоренца, имеем

. (6.14)

Учтем, что 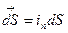, где - единичный вектор внешней нормали на поверхности 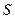. Воспользовавшись правилом перестановки членов в векторно-скалярном произведении, получим

.

Введем формально плотности эквивалентных поверхностных электрических и магнитных токов на поверхности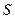

, (6.15)

Формула (6.14) имеет вид:

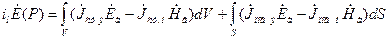. (6.16)

Найдя указанным способом поле , можно вычислить магнитный вектор непосредственно воспользовавшись вторым уравнением Максвелла.

Формула (6.16) выражает принцип, получивший название теоремы эквивалентности.

Если источники внутри объема отсутствуют, то

. (6.17)

Согласно данному выражению, действие источников поля, находящихся вне объема , эквивалентно некоторому распределению поверхностных электрических и магнитных токов на поверхности .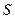

Равенство (6.17) часто используют для расчета апертуры антенн, задавая в том или ином виде распределение эквивалентных поверхностных токов в раскрыве. В рамках такого подхода не удается радикально снизить сложность решения поставленной задачи, т.к. приходится находить векторы вспомогательного электромагнитного поля.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)