Функция Бесселя

Функции Бесселя в математике, это семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя:

где 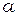- произвольное действительное число, называемое порядком.

Наиболее часто используемые функции Бесселя - функции целых порядков.

Хотя 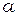и (- 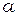) порождают одинаковые уравнения, обычно договариваются о том, чтобы им соответствовали разные функции (это делается, например, для того, чтобы функция Бесселя была гладкой по ).

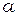Функции Бесселя впервые были определены швейцарским математиком Даниилом Бернулли, а названы в честь Фридриха Бесселя.

Уравнение Бесселя возникает во время нахождения решений Лапласа и уравнения Гельмгольца в цилиндрических и сферических координатах. Поэтому функции Бесселя применяются при решении многих задач о распространении волн, статических потенциалах и т. п., например:

• электромагнитные волны в цилиндрическом волноводе;
• теплопроводности в цилиндрических объектах;
• формы колебания тонкой круглой мембраны
• распределение интенсивности света, дифрагированного на круглом отверстии.
• скорость частиц в цилиндре, заполненном жидкостью и вращающемся вокруг своей оси.

Функции Бесселя применяются и в решении других задач, например, при обработке сигналов.

Функциями Бесселя первого рода, обозначаемыми , являются решения, конечные в точке x = 0 при целых или неотрицательных 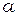. Выбор конкретной функции и её нормализации определяются её свойствами. Можно определить эти функции с помощью разложения в ряд Тейлора около нуля (или в более общий степенной ряд при нецелых ):

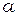Здесь 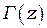- это гамма-функция Эйлера, обобщение факториалф на нецелые значения. График функции Бесселя похож на синусоиду, колебания которой затухают пропорционально , хотя на самом деле нули функции расположены не периодично.

Ниже приведены графики для 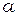= 0,1,2:

Позиция № 251

в плане издания

учебной литературы

МГУ на 2010 г.

Учебное издание

Юрий Дмитриевич Воробьёв

Волновая оптика Дифракция

Учебное пособие

Печатается в авторской редакции

9,3 уч.-изд. л. Формат 60 ´ 84 1/16

Тираж 100 экз. Заказ №

Отпечатано в типографии РПК МГУ им. адм. Г. И. Невельского

690059, Владивосток, ул. Верхнепортовая, 50а

Поиск по сайту: