Метод зон Френеля

Суммирование (интегрирование) амплитуд элементарных колебаний, приходящих в точку , вообще говоря, весьма сложно. Но в простейших случаях, обладающих определенной симметрией, интегрирование, как показал Френель, может быть заменено простым алгебраическим или графическим сложением (последнее особенно наглядно). Суммирование амплитуд колебаний, приходящих от различных элементов волновой поверхности , Френель предложил делать с помощью разбиения волновой поверхности на зоны, конфигурация которых зависит от симметрии рассматриваемой задачи. Пользуясь методом Френеля, определим амплитуду световых колебаний в точке за круглым отверстием на его оси (рис. 3.1).

Если рассматривать точечный источник света S, то в качестве поверхности удобно взять сферу , совпадающую со сферическим фронтом волны, излученной источником . На рис. 3.1 показана часть этого волнового фронта. Рассмотрим в произвольной точке амплитуду световой волны, распространяющейся в однородной среде из точечного источника S. Согласно принципу Гюйгенса-Френеля, заменим действие источника S действием воображаемых источников, расположенных на вспомогательной поверхности , являющейся поверхностью фронта волны, идущей из S. Очевидно, что на сферической поверхности амплитуды и фазы колебаний вторичных источников будут одинаковы, поэтому, остаётся учесть только изменение фазы из-за разности хода от различных точек волнового фронта до точки М.

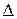Разобьём волновую поверхность на кольцевые зоны, такого размера, чтобы расстояния от краев зоны до точки отличались на . Так как связь между разностью фаз разностью хода определяется выражение

, (3.1)

то при разности хода 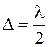разность фаз равна . Поэтому вторичные волны, излучаемые с краёв зон, приходят в точку в противофазе и гасят друг друга.

Можно показать, что площади всех зон Френеля одинаковы и приближённо равны:

(3.2)

где 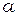- длина отрезка - радиус сферы , - длина отрезка – расстояние от поверхности волнового фронта до точки наблюдения, поэтому вклад в суммарную амплитуду каждой зоны будут примерно одинаковы.

Рис. 3.1. Схема построения зон Френеля

Угол 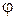между нормалью к поверхности волнового фронта и направлением на точку Р растёт с ростом , поэтому амплитуда колебаний возбуждаемых -ной зоной убывает с ростом , и при число зон и тогда . Это значит, что амплитуды колебаний, возбуждаемые зонами Френеля, образуют слабо убывающую последовательность

(3.3)

Поскольку разность хода от краёв зон равна то, фазы колебаний, возбуждаемых соседними зонами, отличаются на , т.е. находятся в противофазе. Это значит что колебания, возбуждаемые первой зоной, будут подавляться колебания возбуждаемыми второй зоной, колебания второй зоны колебаниями третьей зоной и т.д. Амплитуда результирующего колебания, при 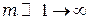, может быть представлена в виде:

(3.4)

Последний член равен нулю, потому что угол между нормалью к излучающей волновой поверхности и направлением на точку наблюдения становится равным и угловой коэффициент , т. е. этот элемент поверхности не излучаете волн в направлении на точку наблюдения.

Заметим, что в выражении (3.4) все амплитуды от нечётных зон входят со знаком плюс, а от чётных зон со знаком минус. Пусть открытыми у нас будет зон. Перепишем выражение (3.4) в другом виде:

(3.5)

где амплитуда последней открытой зоны. Поскольку амплитуда возбуждаемых колебаний монотонно убывает можно приближённо считать что:

. (3.6)

Тогда выражения в скобках равны нулю и если нечётное число, то в центре будет светлое пятно за счёт дополнительно вклада , а если чётное – то в центре тёмное пятно из–за вычитания амплитуды создаваемой последней открытой зоны .

При , угловой коэффициент , поэтому и из формулы (3.5) следует:

. (3.7)

Из формулы (3.7) следует глобальный вывод: когда волновой фронт полностью открыт (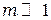) результирующая амплитуда, от всего волнового фронта, равна половине амплитуде создаваемой первой зоной.Это значит, что при свободном распространении волны волновое возмущение от всего волнового фронта составляет половину возмущения, даваемого только первой зоной Френеля. Дело происходит так, как если бы из всего волнового фронта действующей осталось только часть первой зоны Френеля.

Рассмотренные выше рассуждения, выполненные Френелем, можно расценивать как алгебраический способ определения амплитуды световой волны. Кроме этого существует более наглядный графический способ, основанный на методе вращающего вектора амплитуды или методе векторных диаграмм.

4. Векторные диаграммы
Спираль Френеля

Введение зон Френеля позволяет графически анализировать дифракционные явления. Вычисление результирующего светового поля, описываемого интегралом Гюйгенса-Френеля (2.1), по сути дела сводится к суммированию световых колебаний, возбуждаемых элементарными вторичными источниками. С математической точки зрения задача сводится к суммированию гармонических колебаний, имеющих одну и же частоту, но разные амплитуды и фазы. Это можно сделать графическим способом с помощью построения спирали Френеля.

Рассмотрим графический метод сложения амплитуд. В этом простом и наглядном методе полуволновую зону Френеля мысленно разбивают на весьма узкие кольцевые подзоны. Амплитуду колебаний, создаваемых каждой из таких подзон, изобразим элементарным вектором . Вследствие увеличения расстояния 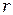и уменьшения коэффициента ,амплитуда колебаний, создаваемых каждой следующей узкой кольцевой зоной, будет убывать по модулю и отставать по фазе от колебаний, создаваемых предыдущей зоной. Изобразив отставание по фазе поворотом каждого вектора против часовой стрелки на соответствующий угол, получим цепочку векторов, векторная сумма которых и есть результирующая амплитуда колебаний в точке Р.

На рис. 4.1а показан результат действия 1-й зоны Френеля. Здесь амплитуда колебаний от узкого кольца, прилегающего к границе 1-й зоны Френеля, отстает по фазе на от амплитуды колебаний, приходящих в точку из центра 1-й зоны — от поэтому соответствующие этим амплитудам векторы взаимно противоположны по направлению.

Рис. 4.1. Рис. 4.2.

Продолжая построение, получим векторную диаграмму для результирующей амплитуды колебаний в точке Р от действия первых двух зон Френеля (рис. 4.1б), затем от первых трех зон Френеля (рис. 4.1в) и т. д.Цепочка по мере увеличения числа узких кольцевых зон будет закручиваться в спираль. В результате амплитуда от действия всех зон (всей волновой поверхности) будет равна вектору , соединяющему начало первой зоны с точкой F – фокусом спирали (рис. 4.2). Длина этого вектора, т.е. амплитуда колебаний в точке Р от полностью открытой волновой поверхности, согласно представлениям Френеля, равна ,а интенсивность в четыре раза меньше, чем при наличии экрана с круглым отверстием, открывающем только 1-ю зону Френеля.

Эту спираль называют спиралью Френеля. Забегая вперед, отметим, что в эксперименте дифракция Френеля связана с действием лишь нескольких первых витков спирали.

Таким образом, амплитуда колебаний и интенсивность света в точке по мере увеличения радиуса отверстия в экране изменяется не монотонно. Пока открывается первая зона Френеля, амплитуда в точке увеличивается и достигает максимума при полностью открытой зоне (см. рис. 4.1а). Но по мере открывания второй зоны Френеля амплитуда колебаний в точке убывает, и при полностью открытых двух первых зонах уменьшается почти до нуля (рис. 4.1б). Затем амплитуда увеличивается снова (рис.4.1в) и т. д. То же самое будет наблюдаться, если вместо увеличения отверстия приближать к нему точку наблюдения вдоль прямой РО (см. рис. 3.1). Это легко понять из данного рисунка: при этом число открываемых зон Френеля в отверстии экрана будет увеличиваться.

На первый взгляд эти результаты, предсказанные на основе принципа Гюйгенса - Френеля, выглядят парадоксальными. Однако они хорошо подтверждаются опытом. В то же время согласно геометрической оптике интенсивность света в точке не должна зависеть от радиуса отверстия. Особенно неожиданным в методе Френеля представляется тот удивительный вывод, чтопри отверстии в экране, открывающем для точки две зоны Френеля, интенсивность в этой точке падает практически до нуля, хотя световой поток через отверстие оказывается вдвое больше (рис. 9б).

Таким образом, как следует из рис. 4.2 амплитуда результирующего поле в точке 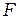(фокусе спирали Френеля) при 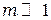равна:

. (4.1)

Поиск по сайту: