Расчёт радиуса зон Френеля

Для наблюдения дифракции необходимо иметь источник света, экран с отверстием и экран для наблюдения. Пусть у нас будет точечный монохроматический источник . В этом случае, как и на рис. 3.1, волновая поверхность будет сферой радиуса 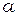. Разобьём эту волновую поверхность на полуволновые зоны Френеля и рассчитаем радиус 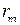произвольной -ой зоны (). Из треугольника DАBC (рис. 5.1):

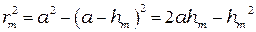. (5.1)

А из треугольника DCBP:

. (5.2

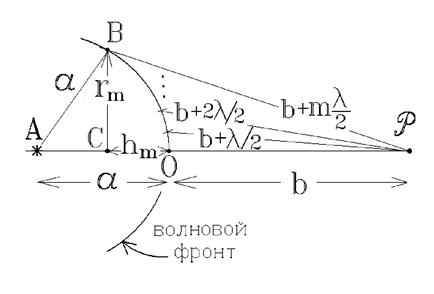
Рис. 5.1.

Так как 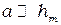и 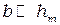при решении полученной системы уравнений можно пренебречь малыми членами и .

Выразим из первого уравнения 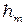, подставим во второе, и решим его относительно .

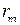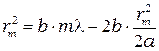
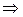
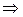
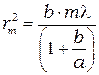
Отсюда:

, (5.3)

Мы получили очень важную формулу, которой будем часто пользоваться при решении задач по дифракции.

Заметим, если падающая на данное отверстие волна плоская (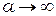), то радиус зоны рассчитывается по формуле:

, (5.4)

так как .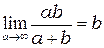

Отсюда также следует (из формулы (5.4)), формула для числа полуволновых зон Френеля при заданном расстоянии от поверхности волновой поверхности до экрана :

(5.5)

Таким образом, число полуволновых зон пропорционально квадрату радиуса отверстия () и обратно пропорционально расстояния от отверстия до экрана (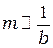). Это значит, что число зон увеличивается при увеличении радиуса отверстия, но уменьшается при увеличении расстояния от отверстия до экрана.

Сделаем оценку размера зон Френеля. Пр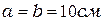и и 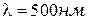радиус первой зоны 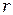= 0,158 мм. Следовательно, распространение света от S к Р происходит так, будто световой поток распространяется внутри очень узкого канала вдоль SР, т.е. прямолинейно.

Таким образом, принцип Гюйгенса-Френеля позволяетобъяснить прямолинейное распространение света в однородной среде.

Поиск по сайту: