Дифракционный интеграл Френеля

Принцип Гюйгенса-Френеля позволяет построить элементарную теорию дифракции света. Основная задача теории дифракции ставится так. Пусть имеется точечный источник света S. Требуется найти световое поле в некоторой точке Р, если между точками S и Р расположено препятствие распространению света, например экран с отверстием или непрозрачный диск. Сначала рассмотрим математическую формулировку принципа Гюйгенса-Френеля.

Введем некоторую произвольную замкнутую поверхность , охватывающую источник света, и будем считать каждый элемент этой поверхности источником вторичной сферической световой волны (Рис. 2.1) рассмотрим некоторую точку М на поверхности . Считая источник света точечным, обозначим расстояние от до через , а расстояние от до точки наблюдения через 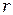. Введем также угол 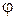между нормалью к поверхности в точке и направлением на точку наблюдения . Для простоты будем считать, что источник света испускает монохроматическую волну.

Рис. 2.1. К выводу интеграла Гюйгенса – Френеля

Принцип Гюйгенса-Френеля утверждает, что световое поле в точке - есть результат наложения (сложения) световых волн, испускаемых всеми элементами поверхности . Волну, испускаемую элементом поверхности , можно считать сферической. Поэтому можно записать, что суммарная амплитуда электрического поля в точке :

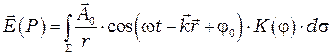
где - уравнение сферической волны, испускаемой элементом поверхности , 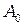- константа равная амплитуде при (размерность 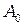), Используя формулу Эйлера, запишем эту же формулу в комплексном виде:

(2.1)

Здесь и — комплексные амплитуды поля в точках Р и М; и - частота и волновое число световой волны, - "коэффициент наклона", монотонно убывающий от некоторого начального значения до нуля при изменении угла 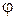от нуля до . Этот коэффициент учитывает то обстоятельство, что вклад элемента в результирующее поле зависит от ориентации данного элемента поверхности по отношению к направлению на точку наблюдения. Из теории Кирхгофа, приближённого решения волнового уравнения Максвелла, следует, что . Для параксиальных пучков света, когда угловой коэффициент .

Интеграл (2.1) называют интегралом Гюйгенса-Френеля. Формула (2.1) получена на основе качественных физических соображений. Множитель в подынтегральном выражении описывает распространение элементарной вторичной сферической световой волны в пространстве. Наиболее существенно то, что интеграл Гюйгенса-Френеля учитывает фазы элементарных вторичных волн, приходящих в точку от различных элементов поверхности , т.е. принимается во внимание интерференция вторичных волн.

Суть принципа Гюйгенса—Френеля записанная в (2.1) в следующем: для определения амплитуды колебания в точке , лежащей перед некоторой поверхностью , надо найти амплитуды колебаний, приходящих в эту точку от всех элементов поверхности и затем сложить их с учетом амплитуд и фаз. При этом предполагается, что все волны испускаемые элементами поверхности взаимно когерентны. Это необходимое условие для интерференции вторичных волн.

Принцип Гюйгенса-Френеля можно представить в простой и наглядной форме с помощью векторной (фазовой) диаграммы (рис. 2.2). Использование подобных диаграмм в дальнейшем позволит значительно упростить многие рассуждения и расчеты. На этой диаграмме результирующая амплитуда - вектор 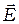, представлен как векторная сумма амплитуд элементарных колебаний в точке от различных элементов поверхности с учетом их фаз, т. е. углов между ними.

Рис. 2.2

Интеграл (2.1) выражает собой математическую формулировку принципа Гюйгенса-Френеля. Взяв этот интеграл можно рассчитать распределение амплитуды световой волны в плоскости наблюдения. Однако практически рассчитать это интеграл оказалось возможным только для самых простых случаев. Френель предложил хотя и приближенный, но изящный способ расчета дифракционных картин, основанный на представлении о так называемых полуволновых зонах или зонах Френеля.

Поиск по сайту: