Дифракция Фраунгофера на щели

Рассмотрим дифракцию Фраунгофера плоской монохроматической волны на одной бесконечно длинной щели шириной 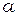(рис. 10.1). Щелью будем называть прямоугольное отверстие, ширина которого во много раз меньше его длины.

Оптическая разность хода между лучами, идущими от краёв щели:

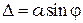(10.1)

Разобьём открытую часть волновой поверхности на полосчатые полуволновые зоны Френеля, параллельные ребру щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна , поэтому на ширине щели уместится 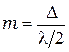зон Френеля.

Поскольку лучи параллельны, то все точки волнового фронта в плоскости щели имеют одинаковую фазу и амплитуду колебаний. Поэтому суммарная интенсивность колебаний от двух любых соседних зон Френеля равна нулю.

Следовательно:

1) если число зон Френеля укладывающихся в щели чётное,

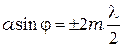(10.2)

то это условие дифракционного минимума.

2) если число зон Френеля нечётное,

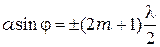(10.3)

- условие дифракционного максимума, соответствующего действию одной некомпенсированной зоны Френеля, где -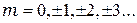

Рис.10.1. Дифракция Фраунгофера на одиночной щели

В направлении 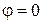щель действует как одна зона Френеля и в этом направлении свет распространяется с наибольшей интенсивностью и формирует центральный дифракционный максимум.

Из (10.2) и (10.3) следует: направления, в которых амплитуда

максимальна 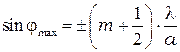(10.4)

минимальна 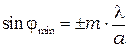(10.5)

Распределение интенсивности на экране, получаемое вследствие дифракции, называется дифракционным спектром. Интенсивности в центральном и последующих максимумах относятся как 1:0,047:0,017:0,0083:..., т.е. основная часть световой энергии сосредоточена в центральном максимуме.

Изменение вида дифракционной картины Фраунгофера при увеличении ширины щели для монохроматического источника света показано на рис. 10.2.

Рис. 10.2. Одномерная дифракция Фраунгофера на вертикальной щели
по мере ее расширения слева направо

Нулевой максимум наиболее яркий и вдвое шире побочных максимумов. Размер области дифракционного расплывания обратно пропорционален ширине щели.

Более точный расчёт дифракции на щели даёт формулу распределения интенсивности света на экране Э в зависимости от угла дифракции 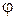виде:

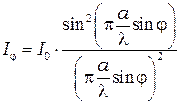(10.6)

где 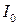- интенсивность света в середине дифракционной картины (в направлении 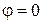); 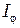- интенсивность света в точке, положение которой определяется данным значением угла 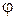. Вид кривой зависимости интенсивности показан на рис. 10.3.

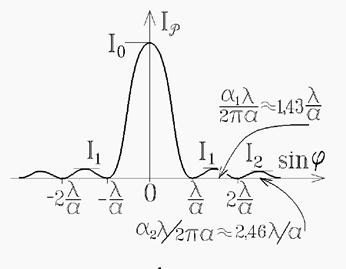
Рис. 10.3

При значении угла дифракции 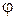, удовлетворяющего условию

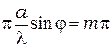(10.7)

интенсивность света равна нулю. Из (10.7) следует уже рассмотренное выше условие главного минимума.

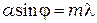(10.8)

где

Условие же максимумов интенсивности отличается от (10.3) и имеет такой вид:

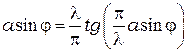. (10.3а)

Однако расчеты показывают, что формула (10.3) по сравнению с (10.3а) дает лишь несущественно завышенные значения угла дифракции : примерно 5% для = 1, на 2% для = 2 и т.д. Такая ошибка пренебрежимо мала, и формулу (10.3) можно считать справедливой. Подставив ее в выражение (10.6), для = 1, 2, 3 и т.д., получим

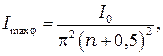
откуда следует, что максимумы 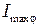высших порядков по сравнению с центральным 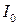очень слабые, а именно:

и т.д.

Из (10.6) вытекает, что . Это означает, что дифракционная картина симметрична относительно центра линзы.

При малых углах дифракции координаты минимумов или максимумов на экране из геометрических соображений можно найти по приближённой формуле. Из рис.10.1 следует, что:

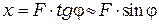
где 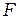- фокусное расстояние линзы. Отсюда 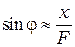и из условий (10.4) и (10.5) получим:

координаты минимумов при дифракции на щели

(10.9)

где = 1, 2, 3,..;

координаты максимумов при дифракции на щели.

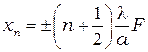(10.10)

где = 0, 1, 2, 3,..

Ширина центрального максимума (рис. 10.1), ограниченная минимумами первого порядка ( = 1), определяется зависимостью

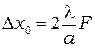. (10.11)

Она увеличивается при уменьшении ширины щели 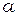, что не может быть объяснено законами геометрической оптики.

При 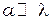дифракция становится слабо выраженной, а на экране наблюдается геометрическое изображение щели. Однако в любом случае дифракцию можно наблюдать только при 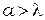. Это следует из формулы (10.5): так как максимальное значение 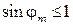, то это возможно при .

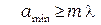На экране, достаточно удалённом (на расстояние L) от щели дифракцию Фраунгофера можно наблюдать и без собирающей линзы Л, для этого необходимо, чтобы выполнялось условие 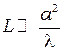. В этом случае формулу (10.11) можно переписать в виде:

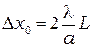. (10.11а)

Пучок света, сходящийся в точке 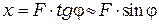экрана, практически остается параллельным. Из формулы (10.4) и (10.5) в этом случае следует, что координаты минимумов и максимумов при дифракции на щели равны соответственно:

координаты минимумов при дифракции на щели

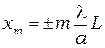(10.12)

где = 1, 2, 3,..; 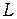- расстояние от плоскости щели до экрана.

координаты максимумов при дифракции на щели.

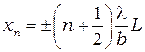(10.13)

где = 1, 2, 3,..

Поиск по сайту: