АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

ДИФРАКЦИОННАЯ РЕШЕТКА КАК СПЕКТРАЛЬНЫЙ ПРИБОР. РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ ДИФРАКЦИОННОЙ РЕШЕТКИ. ДИФРАКЦИЯ БРЭГГА. ДИФРАКЦИЯ НА МНОГИХ БЕСПОРЯДОЧНО РАСПОЛОЖЕННЫХ ПРЕГРАДАХ

Читайте также:
  1. I. Дифракция Фраунгофера на одной щели и определение ширины щели.
  2. III. Дифракция Фраунгофера на мелких круглых частицах.
  3. III. Способность жевать, глотать и употреблять нормальную пищу
  4. V3: Дифракция света
  5. Абстрактное мышление – высокая способность к обучаемости.
  6. Административно-правовой статус субъектов административного права, правоспособность, дееспособность, граждане, иностранные граждане, лица без гражданства, беженцы.
  7. Банкротство и неплатежеспособность. Оценка вероятности банкротства.
  8. Биологические ритмы и работоспособность.
  9. Брегговская дифракция
  10. Важнейшим свойством белка является его способность к гидролизу. При этом разрушаются пептидные связи, разрушается первичная структура белка.
  11. Валентность – это способность атомов присоединять к себе определенное число других атомов.
  12. Виды ионизирующих излучений. Проникающая и ионизирующая способность разных видов ионизирующих излучений

Дифракционной решеткой называется совокупность большого числа одинаковых, отстоящих друг от друга на одно и то же рас­стояние щелей (рис. 3.3.25). Расстояние 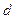между серединами соседних щелей называется периодом решетки.

Расположим параллельно решетке собирающую линзу, в фо­кальной плоскости которой поставим экран. Выясним характер ди­фракционной картины, получающейся на экране при падении на решетку плоской световой волны (для простоты будем считать, что волна падает на решетку нормально). Каждая из щелей даст на экране картину, описываемую кривой, изображенной на рис. 3.3.21. Картины от всех щелей придутся на одно и то же место экрана (независимо от положения щели, центральный максимум лежит против центра линзы). Если бы колебания, приходящие в точку 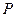от различных щелей, были некогерентными, результирующая картина от щелей отличалась бы от картины, создаваемой одной щелью, лишь тем, что все интенсивности возросли бы в раз. Однако, коле­бания от различных щелей являются в большей или меньшей сте­пени когерентными; поэтому результирующая интенсивность будет отлична от 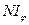( 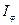- интенсив­ность, создаваемая одной щелью).

В дальнейшем мы будем пред­полагать, что радиус когерентно­сти падающей волны намного пре­вышает длину решетки, так что колебания от всех щелей можно считать когерентными друг отно­сительно друга. В этом случае ре­зультирующее колебание в точ­ке 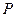, положение которойопределяется углом 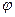, представляет собой сумму колебаний с одинаковой амплитудой 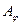, сдвинутых друг относительно друга по фазе на одну и ту же величину . Согласно формуле (3.3.5) интенсивность при этих условиях равна

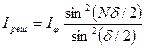(3.3.8)

(в данном случае роль играет ).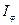

Из рис.3.3.25 видно, что разность хода от соседних щелей равна 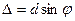. Следовательно, разность фаз

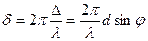, (3.3.9)

где 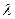- длина волны в данной среде.

Подставив в формулу (3.3.8) выражение (3.3.5) для 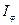и (3.3.9) для , получим

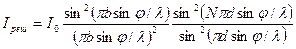(3.3.10)

( - интенсивность, создаваемая одной щелью против центра линзы).


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (2.165 сек.)