 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Уравнение спирали Корню в параметрической форме имеет вид
 ,
,  .
.
Эти интегралы называются интегралами Френеля. Они не берутся в элементарных функциях, однако имеются таблицы, по которым можно находить значения интегралов для разных  .
.
Смысл параметра  заключается в том, что
заключается в том, что  дает длину дуги кривой Корню, измеряемую от начала координат.
дает длину дуги кривой Корню, измеряемую от начала координат.
Числа, отмеченные вдоль кривой на рис. 3.3.13, дают значения параметра  . Точки
. Точки 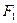 и
и  , к которым асимптотически приближается кривая при стремлении
, к которым асимптотически приближается кривая при стремлении  к
к 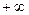 и
и  , называются фокусами или полюсами спирали Корню. Их координаты равны
, называются фокусами или полюсами спирали Корню. Их координаты равны

 ,
, 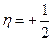 для точки
для точки 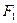 ,
,
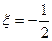 ,
,  для точки
для точки  .
.
Правый завиток спирали (участок  ) соответствует зонам, расположенным справа от точки
) соответствует зонам, расположенным справа от точки 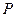 , левый завиток (участок
, левый завиток (участок  ) - зонам, расположенным слева от точки
) - зонам, расположенным слева от точки 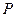 .
.
Найдем производную  в точке кривой, отвечающей данному значению параметра
в точке кривой, отвечающей данному значению параметра  . Приращению
. Приращению  на
на  соответствует
соответствует
 ,
,  .
.
Следовательно,  . Вместе с тем
. Вместе с тем 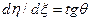 , где
, где  - угол наклона касательной к кривой в данной точке. Таким образом,
- угол наклона касательной к кривой в данной точке. Таким образом,
 .
.
Отсюда следует, что в точке, отвечающей 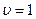 , касательная к кривой Корню перпендикулярна к оси
, касательная к кривой Корню перпендикулярна к оси  . При
. При  угол
угол  равен
равен  , так что касательная параллельна оси
, так что касательная параллельна оси  . При
. При  угол
угол  равен
равен 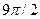 , так что касательная снова перпендикулярна к оси
, так что касательная снова перпендикулярна к оси  , и т. д.
, и т. д.
Спираль Корню дает возможность найти амплитуду светового колебания в любой точке экрана. Положение точки будем характеризовать координатой  , отсчитываемой от границы геометрической тени (см. рис. 3.3.9). Для точки
, отсчитываемой от границы геометрической тени (см. рис. 3.3.9). Для точки 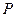 , лежащей на границе геометрической тени
, лежащей на границе геометрической тени  , все штрихованные зоны будут закрыты. Колебаниям от не штрихованных зон соответствует правый завиток спирали. Следовательно, результирующее колебание изобразится вектором, начало которого находится в точке
, все штрихованные зоны будут закрыты. Колебаниям от не штрихованных зон соответствует правый завиток спирали. Следовательно, результирующее колебание изобразится вектором, начало которого находится в точке  , а конец - в точке
, а конец - в точке 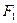 (рис. 3.3.14, а). При смещении точки
(рис. 3.3.14, а). При смещении точки 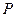 в область геометрической тени полуплоскость закрывает все большее число не штрихованных зон. Поэтому начало результирующего вектора перемещается по правому завитку в направлении полюса F 1 (рис. 3.3.14, б). В результате амплитуда колебания монотонно стремится к нулю.
в область геометрической тени полуплоскость закрывает все большее число не штрихованных зон. Поэтому начало результирующего вектора перемещается по правому завитку в направлении полюса F 1 (рис. 3.3.14, б). В результате амплитуда колебания монотонно стремится к нулю.
Если точка  смещается от границы геометрической тени вправо, в дополнение к не штрихованным зонам открывается все возрастающее число штрихованных зон. Поэтому начало результирующего вектора скользит по левому завитку спирали в направлении к полюсу
смещается от границы геометрической тени вправо, в дополнение к не штрихованным зонам открывается все возрастающее число штрихованных зон. Поэтому начало результирующего вектора скользит по левому завитку спирали в направлении к полюсу  . При этом амплитуда проходит через ряд максимумов (первый из них равен длине отрезка
. При этом амплитуда проходит через ряд максимумов (первый из них равен длине отрезка  на рис.3.3.14, в) и минимумов (первый из них равен длине отрезка
на рис.3.3.14, в) и минимумов (первый из них равен длине отрезка  на рис. 3.3.14, г). При полностью открытой волновой поверхности амплитуда равна длине отрезка
на рис. 3.3.14, г). При полностью открытой волновой поверхности амплитуда равна длине отрезка  (рис. 3.3.14, д), т. е. ровно в два раза превышает амплитуду на границе геометрической тени (см. рис. 3.3.14, а). Соответственно интенсивность на границе геометрической тени составляет 1/4 интенсивности
(рис. 3.3.14, д), т. е. ровно в два раза превышает амплитуду на границе геометрической тени (см. рис. 3.3.14, а). Соответственно интенсивность на границе геометрической тени составляет 1/4 интенсивности  , получающейся на экране в отсутствие преград.
, получающейся на экране в отсутствие преград.
Зависимость интенсивности света  от координаты
от координаты  дана на рис. 3.3.15. Из рисунка видно, что при переходе в область геометрической тени интенсивность изменяется не скачком, а постепенно стремится к нулю. Справа от границы геометрической тени расположен ряд чередующихся максимумов и минимумов интенсивности.
дана на рис. 3.3.15. Из рисунка видно, что при переходе в область геометрической тени интенсивность изменяется не скачком, а постепенно стремится к нулю. Справа от границы геометрической тени расположен ряд чередующихся максимумов и минимумов интенсивности.
 Вычисления дают, что при
Вычисления дают, что при  м и
м и 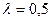 мкм координаты максимумов (см. рис.3.3.15) имеют следующие значения:
мкм координаты максимумов (см. рис.3.3.15) имеют следующие значения:  мм,
мм, 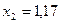 мм,
мм,  мм,
мм,  мм и т. д. С изменением расстояния
мм и т. д. С изменением расстояния  от полуплоскости до экрана значения координат максимумов и минимумов изменяются как
от полуплоскости до экрана значения координат максимумов и минимумов изменяются как 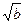 . Из приведенных данных следует, что максимумы располагаются довольно густо. С помощью кривой Корню можно также найти относительную величину интенсивности в максимумах и минимумах. Для первого максимума получается значение
. Из приведенных данных следует, что максимумы располагаются довольно густо. С помощью кривой Корню можно также найти относительную величину интенсивности в максимумах и минимумах. Для первого максимума получается значение  , для первого минимума
, для первого минимума  .
.
 Дифракция от щели. Бесконечно длинную щель можно образовать, расположив рядом две обращенные в разные стороны полуплоскости. Следовательно, задача о дифракции Френеля от щели может быть решена с помощью спирали Корню. Волновую поверхность падающего света, плоскость щели и экран, на котором наблюдается дифракционная картина, будем считать параллельными друг другу (рис.3.3.16).
Дифракция от щели. Бесконечно длинную щель можно образовать, расположив рядом две обращенные в разные стороны полуплоскости. Следовательно, задача о дифракции Френеля от щели может быть решена с помощью спирали Корню. Волновую поверхность падающего света, плоскость щели и экран, на котором наблюдается дифракционная картина, будем считать параллельными друг другу (рис.3.3.16).
Для точки 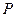 , лежащей против середины щели, начало и конец результирующего вектора находятся в симметричных относительно начала координат точках спирали (рис. 3.3.17). Если сместиться в точку
, лежащей против середины щели, начало и конец результирующего вектора находятся в симметричных относительно начала координат точках спирали (рис. 3.3.17). Если сместиться в точку  , лежащую против края щели, начало результирующего
, лежащую против края щели, начало результирующего
вектора переместится в середину спирали  . Конец вектора переместится по спирали в направлении полюса
. Конец вектора переместится по спирали в направлении полюса 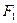 . При углублении в область геометрической тени начало и конец результирующего вектора будут скользить по спирали и в конце концов окажутся на наименьшем расстоянии друг от друга (см. на рис. 3.3.17 вектор, соответствующий точке
. При углублении в область геометрической тени начало и конец результирующего вектора будут скользить по спирали и в конце концов окажутся на наименьшем расстоянии друг от друга (см. на рис. 3.3.17 вектор, соответствующий точке  ). Интенсивность света достигнет при этом минимума. При дальнейшем скольжении по спирали начало и конец вектора снова отойдут друг от друга и интенсивность будет расти. То же самое будет происходить при смещении из точки
). Интенсивность света достигнет при этом минимума. При дальнейшем скольжении по спирали начало и конец вектора снова отойдут друг от друга и интенсивность будет расти. То же самое будет происходить при смещении из точки 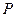 в противоположную сторону, так как дифракционная картина симметрична относительно середины щели.
в противоположную сторону, так как дифракционная картина симметрична относительно середины щели.
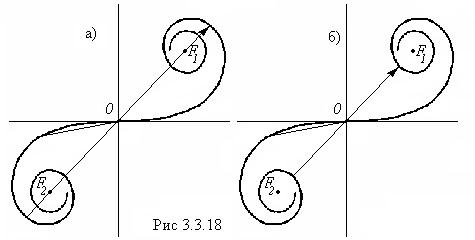
 Если изменять ширину щели, сдвигая полуплоскости в противоположные стороны, интенсивность в средней точке
Если изменять ширину щели, сдвигая полуплоскости в противоположные стороны, интенсивность в средней точке 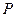 будет пульсировать, проходя попеременно через максимумы (рис. 3.3.18, а) и отличные от нуля минимумы (рис.3.3.18, б).
будет пульсировать, проходя попеременно через максимумы (рис. 3.3.18, а) и отличные от нуля минимумы (рис.3.3.18, б).
Итак, френелевская дифракционная картина от щели представляет собой либо светлую (в случае, изображенном на рис. 3.3.18, а), либо относительно темную (в случае, изображенном на рис. 3.3.18, б) центральную полосу, по обе стороны которой располагаются симметричные относительно нее чередующиеся темные и светлые полосы.
При большой ширине щели начало и конец результирующего вектора для точки 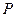 лежат на внутренних витках спирали вблизи полюсов
лежат на внутренних витках спирали вблизи полюсов  и
и  . Поэтому интенсивность света в точках, расположенных против щели, будет практически постоянной. Только на границах геометрической тени образуется система густо расположенных узких светлых и темных полос.
. Поэтому интенсивность света в точках, расположенных против щели, будет практически постоянной. Только на границах геометрической тени образуется система густо расположенных узких светлых и темных полос.
 Заметим, что все полученные в данном параграфе результаты справедливы при условии, что радиус когерентности падающей на преграду световой волны намного превосходит характерный размер преграды (диаметр отверстия или диска, ширину щели и т. п.).
Заметим, что все полученные в данном параграфе результаты справедливы при условии, что радиус когерентности падающей на преграду световой волны намного превосходит характерный размер преграды (диаметр отверстия или диска, ширину щели и т. п.).
Принцип Гюйгенса – Френеля позволяет достаточно просто рассчитать интенсивность света для разных случаев дифракции. При отыскании точных решений необходимо преодоление следующих трудностей, с которыми теория Френеля справиться не могла:
1) в теории Френеля предполагается, что амплитуды и начальные фазы колебаний в точках поверхности, закрытых непрозрачными экранами, такие же, как и в отсутствии последних. Это предположение неправильно, так как граничные условия в точках поверхности экрана зависят от его материала.
2) Теория Френеля дает неправильное значение фазы результирующей волны. Для того, чтобы избежать этой ошибки, в фазе надо считать, что колебания всех вторичных источников, расположенных вдоль некоторой поверхности S 1 совершаются с опережением по фазе π/2 по сравнению с колебаниями в соответствующих точках поверхности S, вызываемых первичной волной.
3) Теория Френеля базируется на чисто качественном допущении о зависимости амплитуды вторичных волн от угла α между рассматриваемым направлением излучения и нормалью к фронту первичной волны.
Поиск по сайту: