Линейной дисперсией называют величину

,

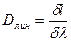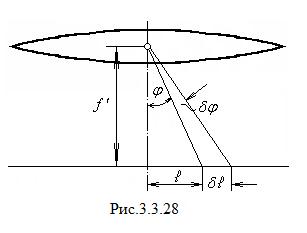где 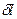- линейное расстояние на экране или на фотопластинке меж­ду спектральными линиями, отличающимися по длине волны на . Из рис. 3.3.28 видно, что при небольших значениях угла 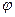можно по­ложить 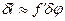, где 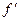- фокусное расстояние линзы, собирающей дифрагирующие лучи на экране. Следовательно, линейная диспер­сия связана с угловой дисперсией 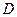соотношением

.

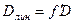Приняв во внимание выражение (3.3.15), получим для линейной дисперсии дифракционной решетки (при небольших 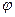) следующую формулу:

.

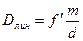Разрешающей силой спектрального прибора называ­ют безразмерную величину

,

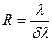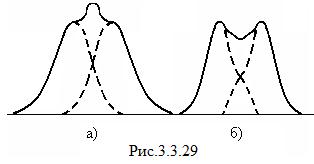где - минимальная разность длин волн двух спектральных ли­ний, при которой эти линии воспринимаются раздельно.

Возможность разрешения (т. е. раздельного восприятия) двух близких спектральных линий зависит не только от расстояний между ними (которое определяется дисперсией прибора), но также и от ширины спектрального максимума. На рис. 3.3.29 показана результирующая интенсивность (сплошные кривые), наблюдающаяся при наложении двух близких максимумов (пунктирные кривые). В случае а) оба максимума воспринимаются как один. В случае б) между максимумами лежит минимум. Два близких максимума вос­принимаются глазом раздельно в том случае, если интенсивность в промежутке между ними составляет не более 80% от интенсивности максимума. Согласно критерию, предложенному Рэлеем, такое соотношение интенсивностей имеет место в том случае, если сере­дина одного максимума совпадает с краем другого (рис. 3.3.29, б). Такое взаимное расположение максимумов получается при определенном (для данного прибора) значении .

Найдем разрешающую силу дифракционной решетки. Положе­ние середины -го максимума для длины волны 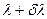определяется условием

.

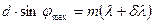Края -го максимума для длины волны 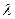расположены под углами, удовлетворяющими соотношению

.

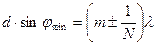Середина максимума для длины волны 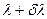совпадет с краем максимума для длины волны 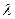в том случае, если

.

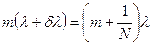Отсюда

.

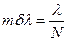Решив это соотношение относительно 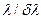, получим выражение для разрешающей силы

.

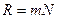Таким образом, разрешающая сила дифракционной решетки про­порциональна порядку спектра и числу щелей .

Дифракционные решетки бывают прозрачные и отражательные. Прозрачные решетки изготавливаются из стеклянных или кварце­вых пластинок, на поверхность которых с помощью специальной машины наносится алмазным резцом ряд параллельных штрихов. Промежутки между, штрихами служат щелями.

Отражательные решетки наносятся ал­мазным резцом на поверхность металличе­ского зеркала. Свет падает на отражатель­ную решетку наклонно. При этом решет­ка с периодом 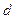действует так, как при нормальном падении света действовала бы прозрачная решетка с периодом 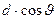, где 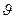- угол падения. Это позволяет на­блюдать спектр при отражении света, на­пример, от грампластинки, имеющей всего несколько штрихов (канавок) на 1 мм, если расположить ее так, чтобы угол падения был близок к 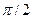. Роуланд изобрел вогну­тую отражательную решетку, которая сама (без линзы) фокусиру­ет дифракционные спектры.

Поставив две дифракционные решетки одну за другой так, чтобы их штрихи были взаимно перпендикулярными. Первая ре­шетка (штрихи которой, скажем, вертикальны) даст в горизон­тальном направлении ряд максимумов, положения которых опре­деляются условием

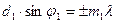
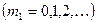. (3.3.16)

Вторая решетка (с горизонтальными штрихами) разобьет каждый из образовавшихся таким образом пучков на расположенные по вертикали максимумы, положения которых определяются условием

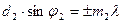
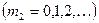. (3.3.17)

В итоге дифракционная картина будет иметь вид правильно распо­ложенных: пятен, каждому из которых соответствуют два целочис­ленных индекса 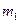и .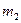

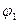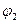Такая же дифракционная картина получается, если вместо двух раздельных решеток взять одну прозрачную пластинку с нанесен­ными на нее двумя системами взаимно перпендикулярных штрихов. Подобная пластинка представляет собой двумерную пери­одическую структуру (обычная решетка - одномер­ную структуру). Измерив углы и , определяющие положения максимумов, и зная длину волны 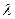, можно найти по формулам (3.3.16) и (3.3.17) периоды структуры 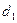и 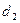. Если направления, в которых структура периодична (например, направления, перпенди­кулярные к штрихам решеток), образуют угол 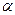, отличный от 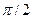, дифракционные максимумы расположатся не в вершинах прямоугольников (как на рис. 3.3.30), а в вершинах параллелограммов. В этом случае по дифракционной картине можно определить не только периоды 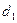и 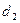, но и угол .

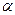Дифракционную картину, аналогичную изображенной на рис.3.3.30, дают любые двумерные периодические структуры, на­пример система небольших отверстий или система непрозрачных маленьких шариков.

Для возникновения дифракционных максимумов необходимо, чтобы период структуры 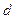был больше 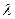. В противном случае усло­вия (3.3.16) и (3.3.17) могут быть удовлетворены только при значе­ниях 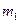и 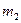, равных нулю (модуль не может превышать единицу).

Дифракция наблюдается также на трехмерных структурах (дифракция Брэгга), т. е. пространственных образованиях, обнаруживающих периодич­ность по трем не лежащим в одной плоскости направлениям. По­добными структурами являются все кристаллические тела. Однако их период 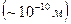слишком мал для того, чтобы можно было наблюдать дифракцию в видимом свете. В случае кристаллов усло­вие 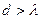выполняется только для рентгеновских лучей. Впервые дифракция рентгеновских лучей от кристаллов наблюдалась в 1913 г. в опыте Лауэ, Фридриха и Книппинга (Лауэ принадлежит идея, остальным авторам - практическое осуществление опыта).

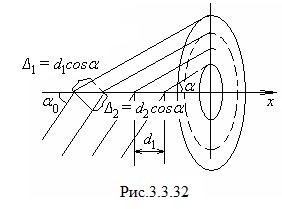
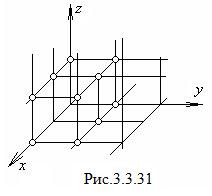Найдем условия образования дифракционных максимумов от трехмерной структуры. Проведем в направлениях, по которым свойства структуры обнаруживают периодичность, координатные оси x, y и z (рис.3.3.31). Структуру можно представить как совокуп­ность равноотстоящих параллельных линейных цепочек из струк­турных элементов, расположенных вдоль одной из координатных осей. Рассмотрим действие отдельной линейной цепочки, параллель­ной, например, оси x (рис. 3.3.32). Пусть на нее падает пучок па­раллельных лучей, образующих с осью x угол 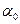. Каждый струк­турный элемент является ис­точником вторичных волн. 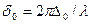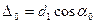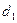К соседним источникам падающая волна приходит с разностью фаз , где ( - период структуры вдоль оси x). Кроме того, между вто­ричными волнами, распростра­няющимися в направлениях, образующих с осью х угол 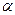(все такие направления лежат вдоль образующих конуса, осью ко­торого служит ось х), возникает дополнительная разность хода 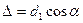. Колебания от различных структурных элементов бу­дут взаимно усиливаться для тех направлений, для которых

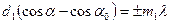
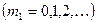. (3.3.18)

Каждому значению 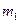соответствует свой конус направлений, вдоль которых получаются максимумы интенсивности от одной отдельно взятой цепочки, параллельной оси x. Ось этого конуса совпадает с осью x.

Условие максимума для цепочки, параллельной оси y, имеет вид

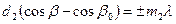
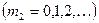, (3.3.19)

где 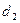- период структуры в направлении оси y, 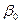- угол между падающим пучком и осью y, 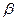- угол, образуемый с осью y направлениями, вдоль которых получаются дифракционные максимумы. Каждому значению 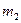соответствует конус направлений, ось которого совпадает с осью y.

В направлениях, удовлетворяющих одновременно условиям (3.3.18) и. (3.3.19), происходит взаимное усиление колебаний от ис­точников, лежащих в одной и той же плоскости, перпендикуляр­ной к оси z (эти источники образуют двумерную структуру). Направления возникающих максимумов интенсивности лежат вдоль линий пересечения конусов направлений, один из которых определяется условием (3.3.18), второй — условием (3.3.19).

Наконец, для цепочки, параллельной оси z, направления макси­мумов определяются условием

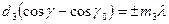
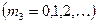, (3.3.20),

где 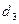- период структуры в направлении оси z, 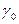- угол между падающим пучком и осью z, 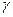- угол образуемый с осью z направ­лениями, вдоль которых получаются дифракционные максимумы. Как и в предыдущих случаях, каждому значению 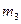соответствует конус направлений, осью которого является ось z.

В направлениях, удовлетворяющих одновременно условиям (3.3.18), (3.3.19) и (3.3.20), происходит взаимное усиление колеба­ний от всех элементов, образующих пространственную структуру. В результате возникают дифракционные максимумы от простран­ственной структуры. Направления этих максимумов лежат на ли­ниях пересечения трех конусов, оси которых параллельны коор­динатным осям.

Найденные нами условия

, ,

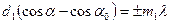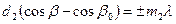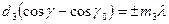
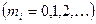(3.3.21)

носят название формул Лауэ. Каждому определяемому эти­ми формулами направлению 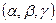соответствуют три целочис­ленных индекса 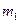, 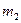и 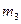. Наибольшее значение модуля раз­ности косинусов равно 2. Поэтому условия (3.3.21) могут быть вы­полнены при отличных от нуля значениях индексов лишь в том случае, если 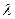не превышает .

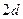Углы 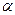, 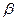и 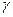не являются независимыми. Например, в случае прямоугольной системы координат они связаны соотношением

.

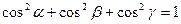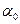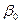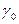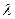Таким образом, при заданных , , и углы 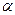, , 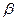, 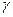определяю­щие направления максимумов, могут быть найдены путем решения системы из четырех уравнений.

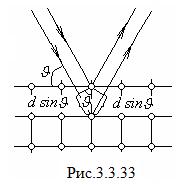
Проведем через узлы кри­сталлической решетки параллельные равноотстоящие плоскости (рис.3.3.33), которые мы будем называть атомными слоями. Если падающая на кристалл волна плоская, огибающая вторичных волн, порождаемых атомами, лежащими в таком слое, также будет представлять собой плоскость. Таким образом, суммарное дейст­вие атомов, лежащих в одном слое, можно представить в виде плоской волны, отразившейся от усеянной атомами поверхности по обычному закону отражения.

Плоские вторичные волны, отразившиеся от разных атомных слоев, когерентны и будут интерферировать между собой подобно волнам, посылаемым в данном направлении различными щелями дифракционной решетки. При этом, как и в случае решетки, вто­ричные волны будут практически погашать друг друга во всех направлениях, кроме тех, для которых разность хода между сосед­ними волнами является кратной 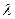. Из рис. 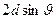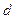3.3.33 видно, что раз­ность хода двух волн, отразившихся от соседних атомных слоев, равна , где - период идентичности кристалла в направле­нии, перпендикулярном к рассматриваемым слоям, 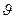- угол, до­полнительный к углу падения и называемый углом скольже­ния падающих лучей. Следовательно, направления, в которых получаются дифракционные максимумы, определяются условием

.

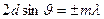
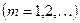Это соотношение называется формулой Брэгга - Вульфа.

Важно отметить, что при фраунгоферовой дифракции распределение интенсивности в дифракционной картине определяется только направлением лучей, а не положением световых пучков. Это означает, что распределение интенсивности не изменится, если отверстия в преграде сместить в сторону без изменения их ориентации.

Особый интерес представляет ситуация, когда в преграде имеется большое число N одинаковых отверстий. Возможны два случая:

1) отверстия расположены хаотично, беспорядочно;

2) отверстия расположены упорядоченно, регулярно.

В первом случае фазовые соотношения между волнами, дифрагированными от отдельных отверстий, имеют случайный характер (волны некогерентны), поэтому для каждого направления наблюдения происходит простое сложение интенсивностей волн, дифрагированных от всех отверстий. Распределение интенсивности в дифракционной картине от одного отверстия не зависит от его положения. От большого числа N отверстий получается такая же картина, но усиленная в N раз.

Во втором случае волны, дифрагированные от соседних отверстий, имеют определенное значение разности фаз и когерентны. Интерференция этих волн существенно изменяет дифракционную картину, образуя резкое увеличение интенсивности в некоторых направлениях (например, в дифракционной решетке).

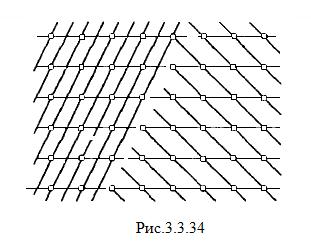
В кристалле можно провести множество атомных плоскостей в различных направлениях (рис.3.4.34). Каждая система плоскостей может дать дифракционный максимум, если для нее будет выполнено условие Вульфа-Брэгга. Однако эффективными являются только такие плоскости, в которых атомы расположены плотно.

Поиск по сайту: