Методика эксперимента. В соответствии с принципом Гюйгенса-Френеля волновое поле, т

В соответствии с принципом Гюйгенса-Френеля волновое поле, т. е. распределение интенсивности света, на экране Э2 (рис.48) рассматривается как результат суперпозиции волн, испущенных «вторичными» источниками, расположенными на волновой поверхности, например, в плоскости экрана Э1 и когерентными с полем падающей волны.

Пусть плоская волна падает нормально на экран Э1 параллельно его оси симметрии ОР. Расчёт показывает, что колебание, приходящее в точку Р из точки В, запаздывает по фазе относительно колебания, приходящего от точки О, на величину

. (66)

Участок волновой поверхности в плоскости экрана Э1, в пределах которого фаза приходящих в точку Р колебаний изменяется на , называется зоной Френеля. Первая зона Френеля - кружок с центром в точке О, для которого . Для второй (кольцевой) зоны и т.д. Условие 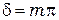определяет количество (целое или дробное) зон, укладывающихся в круге радиуса 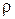‚ или радиус 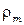участка, на котором укладываются первых зон Френеля (он же – радиус внешней границы m -й зоны):

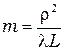(67)

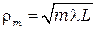(68)

Сопоставляя (67) и (63), отметим, что если 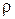- характерный размер отверстия в экране Э1, то число является параметром дифракции, определяющим вид дифракции и дифракционной картины.

Если на экран Э1 падает расходящаяся волна от точечного источника (рис. 49 а) или волна, сходящаяся в точке (рис. 49 б), то вычисления фазовых сдвигов и количества открытых зон Френеля приводят к тем же формулам (66) - (67), что для плоской волны, в которых, однако, 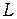выражается через расстояние от фокуса волны до экрана Э1 и расстояние 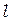от экрана Э1 до экрана Э2.

Для расходящейся волны

(69)

Для сходящейся волны

(70)

Плоской волне, очевидно, соответствует , .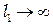

Если в сходящейся волне расстояние 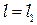, (т.е. картина наблюдается в фокальной плоскости) то 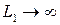и , наблюдается дифракционная картина Фраунгофера. Это обстоятельство очень важно для экспериментального наблюдения дифракции Фраунгофера. В плоской волне не всегда возможно обеспечить значения , достаточные для наблюдения дифракции Фраунгофера. Например, при см. и 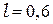мкм. согласно (60) получаем 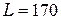м. Тогда дифракцию Фраунгофера наблюдают в фокальной плоскости сходящейся сферической волны.

Пусть в экране Э1 имеется круглое отверстие радиуса 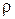. Дифракционная картина симметрична относительно оси отверстия и имеет вид концентрических тёмных и светлых колец. Характер распределения интенсивности зависит от числа зон Френеля , открываемых отверстием. При небольших интенсивность в центре картины равна

(71)

где 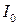- интенсивность в отсутствие экрана Э1.

При нечётном в центре картины наблюдается максимум интенсивности (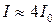), при чётном - минимум. Это обусловлено тем, что чётные и нечётные зоны дают в центре картины противофазные колебания. Угловой размер центрального тёмного или светлого пятна равен углу дифракции .

Дифракционная картина Фраунгофера (при 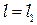) имеет вид центрального светлого пятна, окруженными тёмными и светлыми кольцами. Радиусы первого и двух последующих тёмных колец равны

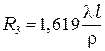(72)

Поиск по сайту: