Методика эксперимента. Наблюдение дифракции Фраунгофера на крупных объектов (более 0,1мм) без использования дополнительной оптики может потребовать слишком больших размеров

Наблюдение дифракции Фраунгофера на крупных объектов (более 0,1мм) без использования дополнительной оптики может потребовать слишком больших размеров установки. Поэтому, как правило, дифракционные картины Фраунгофера наблюдают в фокальной плоскости сходящейся сферической волны.

Пусть плоская волна нормально падает на экран Э1 (Рис. 50), а дифракционная картина наблюдается на экране Э2 в фокальной плоскости линзы Л. (Здесь сохранена нумерация рисунков и формул по учебному пособию - В. В. Светозаров. Модульный оптический практикум: Учебное пособие. М.: ВЛАДИС, 1998. 85 с.) Каждой точке Р в плоскости наблюдения соответствует определённое направление излучения, выходящего из плоскости Э1. Такое же соответствие мы получили бы без линзы Л, если бы удалили экран Э2 на расстояни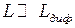е , где - дифракционная длина (расстояние Релея, см раздел 7.).

Амплитуда колебаний в точке Р, в соответствии с принципом Гюйгенса-Френеля, определяется амплитудами и фазами приходящих в эту точку волн, излучённых в соответствующем направлении всеми элементами экрана Э1. В простейшем случае амплитуды определяются коэффициентом пропускания экрана Э1, а фазы - разностью хода 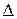(рис. 50).

Такая схема позволяет упростить установку и более гибко варьировать параметры опыта, благодаря чему широко используется в современной когерентной оптике. Непосредственный расчёт дифракционной картины в сходящейся волне сложен, но можно воспользоваться результатами расчёта для классической схемы.

Рассмотрим ещё раз классическую схему (рис. 51а). Согласно принципу Гюйгенса - Френеля амплитуда колебаний в произвольной точке наблюдения Р экрана Э2 определяется амплитудами и фазами колебаний вторичных источников, расположенных на поверхности, отделяющей первичный источник от наблюдателя. Выберем в качестве такой поверхности плоскость , расположенную сразу после линзы. Амплитуды и фазы колебаний в этой плоскости определяются коэффициентом пропускания экрана Э1 и оптической длиной лучей, идущих от источника до плоскости.

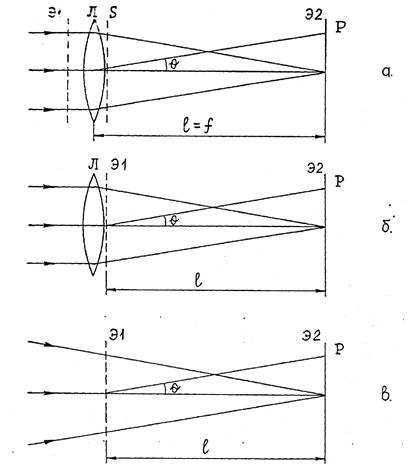
Рис. 51

Указанные амплитуды и фазы не изменятся, если экран Э1 расположить не перед линзой Л, а сразу после неё, совместив его с плоскостью S, как показано на рис.51 б. Не изменится при этом и дифракционная картина на экране Э2. Теперь дифракционная картина полностью определяется экраном Э1 и падающей на него волной. Способ создания волны несуществен. Поэтому оптическая система, создающая сходящуюся волну, может быть какой угодно и расположена где угодно. На рис.51 в эта система вынесена за пределы рисунка.

Зависимость интенсивности излучения на экране Э2 от положения точки Р, или, что то - же, от направления излучения, определяемого углом , в схеме по рис. 51 в будет такой же, как и в классической схеме (рис. 50), с тем лишь различием, что во всех формулах вместо фокусного расстояния линзы 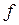будет фигурировать расстояние 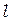между экранами Э1 и Э2.

Поиск по сайту: