 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Дифракция Фраунгофера на круглом отверстии
В этом случае дифракционная картина представляет собой чередование светлых и темных колец. В центре дифракционной картины всегда наблюдается светлое пятно (дифракционный максимум). Распределение интенсивности в плоскости экрана наблюдения задается функцией (рис. 9.2):
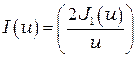
где  - функция Бесселя, первого рода (см. Приложение 6)
- функция Бесселя, первого рода (см. Приложение 6)
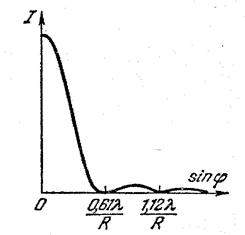
Рис. 9.2
Расчет положения минимумов и максимумов в математическом плане сводится к определению корней функции Бесселя  , где
, где  ,
, 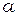 - радиус отверстия.
- радиус отверстия.
Положение максимумов и минимумов удовлетворяют условию:

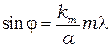
где  = 1, 2, 3, 4,... - порядок максимума или минимума. Значения
= 1, 2, 3, 4,... - порядок максимума или минимума. Значения  ,
,  и относительные интенсивности максимумов
и относительные интенсивности максимумов  для
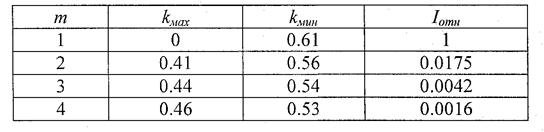
для  = 1, 2, 3, 4 приведены в таблице.
= 1, 2, 3, 4 приведены в таблице.
Поиск по сайту: