АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Критерий дифракции

Читайте также:
  1. VI. Проверка статистических гипотез, критерий Стьюдента
  2. VII. Проверка статистических гипотез, критерий Хи-квадрат
  3. Базовый критерий компоновки
  4. В основу другой классификации положен критерий характера фактора (объективный или субъективный).
  5. Валютный рынок и его роль в определении внутреннего равновесия национальной экономики. Платежный баланс, как критерий внешнего равновесия национальной экономики.
  6. Вопрос 4. Какой критерий анализа хозяйственной деятельности предприятия является генеральным в условиях рыночной экономики?
  7. Главный критерий – эффективность деятельности
  8. Ещё один аспект проявления принципа «практика — критерий истины»: «по вере вашей да будет вам»
  9. Интегральный критерий качества.
  10. Какой критерий лежит в основе определения ПДК на промышленной площадке?
  11. Комплексный (лекальный) критерий
  12. Краткосрочный и долгосрочный спрос на инвестиции. Влияние ставки процента на принятие решений по долгосрочным инвестициям. Критерий чистой дисконтированной стоимости.

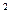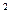Установим количественный критерий, позволяющий определить, какой вид дифракции будет иметь место в каждом конкретном случае. Найдем разность хода лучей от краев щели до точки Р (рис.5). Применим теорему косинусов к треугольнику со сторонами r, r+D и b: (r+D) =r +b 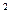-2rbcos(p/2+j).

После несложных преобразований получим

2rD + D 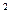= b 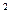+ 2rbsinj. (5.21)

Нас интересует случай, когда лучи, идущие от края щели в точку Р, почти параллельны. При этом условие D2 << rD, поэтому в уравнении (5.21) можно пренебречь слагаемым D2. В этом приближении

D=b2/2r+bsinj. (5.22)

 

 
 


j D

 

r r + D l

 

P

Рис.5.8

В пределе при r®¥ получается значение разности хода D ∞ = bsinj, совпадающие с выражением, фигурирующим в формуле(5.16).

При конечных r характер дифракционной картины будет определяться соотношением между разностью D - D ∞ и длиной волны l. Т.е.. характер дифракции зависит от значения безразмерного параметра

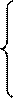b2/(l l) (5.23)

<<1 – дифракция Фраунгофера,

Если b2/ l l = ~1 – дифракция Френеля,

>>1 – геометрического оптика.

Параметру (5.23) можно дать наглядное истолкование. Возьмем точку Р, лежащую против середины щели рис.5.9.

b

 

 

l l+m .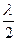

 

 

P

Рис. 5.9.

Для этой точки число m открываемых щелью зон Френеля определяется соотношением (l + ml/ 2)2 = l 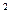+ (b/2)2. Раскрыв скобки и отбросив слагаемое, пропорциональное l2, получим

m = b2/4ll ~ b2/ll (5.24).

Таким образом, параметр (5.23) непосредственно связан с числом открытых зон Френеля (для точки, лежащей против середины щели).

Если щель открывает малую долю центральной зоны Френеля (m<<1), наблюдается дифракция Фраунгофера. Если щель открывает небольшое число зон Френеля (m~1), на экране получается изображение щели, обрамленное по краям отчетливо видимыми светлыми и темными полосами. И если щель открывает большое число зон Френеля (m>>1), на экране получается равномерно освещенное изображение щели.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)