Дифракция Френеля. Зоны Френеля

Вычисления по формуле (5.2) представляют собой в общем случае весьма сложную задачу. Однако, для случаев симметричного прохождения света при огибании препятствий, нахождение амплитуды результирующего колебания можно осуществить простым векторным суммированием.

Рассмотрим дифракцию света при прохождении через круглое отверстие. Точечный источник света Ѕ располагается на линии ЅР, проходящей через центр отверстия и перпендикулярно к его плоскости (см. Рис 5.3). В точке Р определим амплитуду светового колебания возбуждаемого сферической волной, распространяющейся в изотропной однородной среде от точечного источника Ѕ.

Волновые поверхности такой волны дошедшие до отверстия симметричны относительно прямой ЅР, радиус этой волновой поверхности пусть будет равен а, тогда оптическая длина пути от вторичного источника до точки наблюдения Р равна b. Разобьем изображенную на рисунке волновую поверхность на кольцевые зоны, построенные так, что расстояния от краев каждой зоны до точки Р различаются на λ/2 (λ – длина волны в той среде, в которой распространяется волна). Обладающие таким свойством зоны носят название зон Френеля.

Рис. 5.3.

Из рис. 5.3 видно, что расстояние b_m от внешнего края m-й зоны до точки Р равно 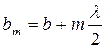(5.3)

Колебания приходящие в точку Р от аналогичных вторичных источников двух соседних зон, находятся в противофазе. Поэтому и результирующее колебании, создаваемое каждой из зон в целом, будут для соседних зон различаться по фазе на π.

Вычислим площади зон. Внешняя граница m-й зоны выделяет на волновой поверхности сферический сегмент высоты h_m (Рис. 5.4).

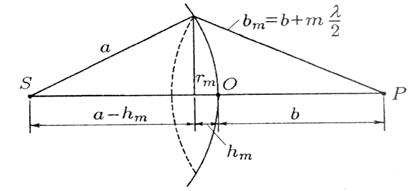
Рис. 5.4.

Обозначим площадь этого сегмента через Ѕ_m. Тогда площадь m-й зоны можно представить в виде ΔЅ_m = Ѕ_m – Ѕ_m–1, где Ѕ_m–1 – площадь сферического сегмента, выделяемого внешней границей (m-1)-й зоны. Из рис. 5.4 видно, что квадрат радиуса m-й зоны.r_m

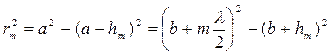
Открыв скобки, получим

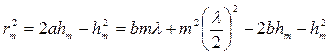(5.4)

откуда

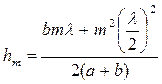(5.5)

Ограничившись рассмотрением не слишком больших m, можно ввиду малости (λ/2)² пренебречь вторым слагаемым. В этом приближении

(5.6)

Площадь сферического сегмента равна Ѕ = 2πRh (R – радиус сферы, h – высота сегмента). Следовательно,

Ѕ_m = 2π а h_m =

А площадь m-й зоны равна ΔЅ_m = Ѕ_m – Ѕ_m–1= Полученное выражение не зависит от m. Это означает, что при не слишком больших m площади зон Френеля примерно одинаковы.

Из равенства (5.4) можно найти радиусы зон. При не слишком больших m высота сегмента h_m«а, поэтому можно считать, что . Подставив значения для h_m (5.6), получим для радиуса внешней границы m-й зоны получим выражение

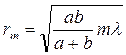(5.7)

Итак, площади зон Френеля примерно одинаковы. Расстояния b_m от зоны до точки Р медленно растет с номером зоны m. Угол φ между нормалью к элементам зоны и направлениям на точку Р также растет с m. Все это приводит к тому, что амплитуда А_m колебания, возбуждаемого m-й зоной в точке Р, монотонно убывает сростом m. Таким образом амплитуда колебаний возбуждаемых в точке Р зонами Френеля образуют монотонно убывающую последовательность

А₁ > А₂ > А₃ > … > А_m-1 > А_m > А_m+1 > …

Фазы колебаний, возбуждаемых соседними зонами, различаются на π. Поэтому амплитуда А результирующего колебания в точке Р может быть представлена в в виде

А = А₁ – А₂ + А₃ – А₄ + … (5.8)

В это выражение все амплитуды от нечетных зон входят с одним знаком, а от четных зон – с другим.

Запишем выражение (5.8) в виде:

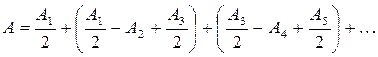(5.9)

Вследствие монотонного убывания А_m можно приближенно саитать, что

Тогда в формуле (5.9) выражение в скобках будут равны нулю, и она упрощается следующим образом:

А = А₁/2. (5.10)

Согласно формуле (5.10) амплитуда, создаваемая в некоторой точке Р, всей сферической волновой поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной. Если на пути волны поставить непрозрачный экран с отверстием, оставляющим открытой только первую зону Френеля, амплитуда в точке Р будет равна А₁, т.е. в два раза превзойдет амплитуду (5.10). Соответственно интенсивность света в точке Р будет в этом случае в четыре раза больше, чем в отсутствие преград между точками S и Р.

Теперь решим задачу о распространении света от источника S к точке Р методом графического сложения амплитуд. Разобьем волновую поверхность на кольцевые зоны, аналогичные зонам Френеля, но гораздо меньшие по ширине (разность хода от краев зоны до точки Р составляет одинаковую для всех зон малую долю λ). Колебание, создаваемое в точке Р каждой из зон, изобразим в виде вектора, длина которого равна амплитуде колебания, а угол, образуемый вектором с направлением, принятым за начало отсчета, дает начальную фазу колебания. Амплитуда колебаний, создаваемых такими зонами в точке Р, медленно убывает при переходе от зоны к зоне. Каждое следующее колебание отстает от предыдущего по фазе на одну и ту же величину. Следовательно, векторная диаграмма, получающая при сложении колебаний0 возбуждаемых отдельными зонами, имеет вид, показанный на рис.5.5. в

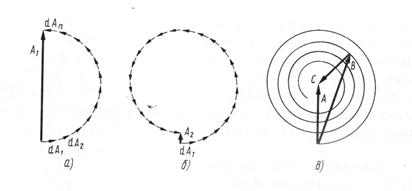
Рис. 5.5

Если бы амплитуды, создаваемые отдельными зонами, были одинаковыми, конец последнего из изображенных на рис.5.5. б векторов совпал бы с началом первого вектора. В действительности значение амплитуды, хотя и очень слабо, но убывает, вследствие чего векторы образуют не замкнутую фигуру, а ломаную спиралевидную линию.

В пределе при стремлении ширины кольцевых зон к нулю (количество их будет при этом неограниченно возрастать) векторная диаграмма примет вид закручивающейся спирали. Фазы колебаний в точках О и 1 различаются на π (бесконечно малые векторы, образующие спираль, направлены в в этих точках в противоположные стороны). Следовательно, участок спирали изображенный на рис 5.5. а соответствует первой зоне Френеля. Колебания от первой и второй зон находятся в противофазе, рис 5.5. б.

Поиск по сайту: