 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ОБРАТНАЯ РЕШЕТКА
Условия наблюдения дифракционных максимумов могут быть записаны в виде векторного уравнения - основного интерференционного уравнения. Это уравнение связывает между собой, с одной стороны, единичные вектора 
и 
, определяющие направления падающего луча, и направление наблюдения и, с другой стороны, вектор обратной решетки.
Обратную решетку вводят для облегчения расчёта дифракционной картины. Её базисные векторы 
, 
, 
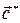задают так, чтобы они были ортогональны разноименным векторам прямой решетки и имели длину, обратную одноименным векторам. Это означает что:
; 
; 
;
.
Такое определение обратной решетки позволяет, с одной стороны, легко построить ее, если известны базисные вектора прямой решетки (и, соответственно, наоборот), а, с другой стороны, придают ей ценные свойства, которые легко можно доказать, пользуясь правилами векторной алгебры. Для изложения важно то, что плоскости (hkl) прямой решетки в обратной решетке соответствует узел с координатами h, k, l: [[ hkl ]]* и что модуль вектора обратной решетки равен обратной величине расстояния dhkl между плоскостями {hkl} прямой решётки, т.е.
Используя понятие обратной решетки, векторное условие наблюдения максимума дифракционной картины можно представить в виде уравнения (основного интерференционного уравнения):
.
В справедливости приведённого уравнения нетрудно убедиться, сравнив его с системой уравнений (1). Легко увидеть, что и условия Лауэ и уравнение Вульфа-Брэгга содержатся в этом уравнении. Например, умножив скалярно основное интерференционное уравнение на базисный вектор прямой решетки 
, получим условие Лауэ для цепочки атомов в направлении вектора :
®
.
Геометрический способ решения основного интерференционного уравнения известен как построение Эвальда. Построение сводится к тому, что в пространстве обратной решетки строят сферу радиуса 
(сферу Эвальда). При этом направление падающего луча должно совпадать с её диаметром, а сфера должна пересекаться с направлением падающего пучка в узле обратной решетки. Узлы обратной решетки, оказавшиеся на сфере, с одной стороны, связаны между собой векторами обратной решетки, а, с другой стороны, являются разностью векторов 
и 
. Таким образом, вектор по построению 
задаёт направление, в котором будет наблюдаться максимум дифракционной картины (рис.10).
Поиск по сайту: