 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ДИФРАКЦИЯ ВОЛН НА ТРЕХМЕРНЫХ РЕШЕТКАХ
Из опытов по дифракции рентгеновских лучей на кристаллах следовало, что кристаллы можно рассматривать как пространственные решетки с периодом того же порядка что и длина волны рентгеновского излучения и для анализа экспериментальных данных использовать общепринятую теорию дифракции. В качестве примера анализа экспериментальных результатов по дифракции на трёхмерных решётках рассмотрим рассеяние рентгеновских лучей на кристаллах.
Пусть на одномерную цепочку атомов падает пучок параллельных рентгеновских лучей. Попадая в периодически изменяющееся поле электромагнитной волны
E(t)=Em cos(wt-kx),
электроны атомов начинают совершать вынужденные колебания, так как на них действует периодически меняющаяся вынуждающая сила
.
Под действием этой силы электроны движутся с переменным ускорением
и вследствие этого становятся источниками переменного электромагнитного поля. В соответствии с законами электродинамики, это приводит к вынужденному излучению электромагнитных волн. Таким образом, каждый атом, попавший в поле рентгеновского излучения, сам становится источником вторичных волн, частота которых совпадает с частотой возбуждающего излучения. Для простоты будем считать вторичные волны сферическими. Это предположение, конечно, не позволит описать результаты эксперимента во всех деталях. Однако наиболее яркие черты явления охватываются достаточно верно.
Приходя в точку наблюдения, вторичные волны интерферируют. Длина пути от источника излучения до атома цепочки и от атома до точки наблюдения зависит от положения атома. Поэтому разность хода D для интерферирующих лучей будет зависеть как от угла между падающим пучком и цепочкой атомов (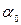
), так и от угла между цепочкой атомов и направлением на точку наблюдения (
) (рис.7). Как видно из рисунка
,
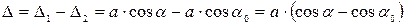где a - модуль базисного вектора.
 |
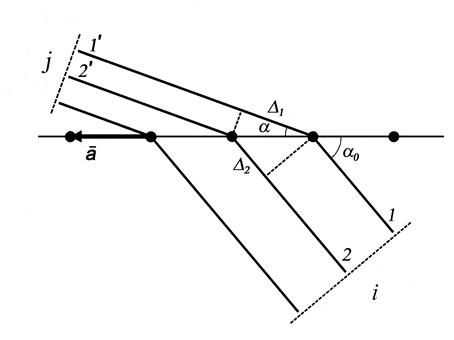
Известно, что максимум интерференционной картины будет наблюдаться, когда разность хода между лучами составит целое число длин волн:
, где n - любое целое число.
Если рассмотреть теперь трехмерную решетку атомов, то для неё должны одновременно выполняться условия максимума дифракционной картины в направлении каждого из базисных векторов:
,
, (1)
.
Будем характеризовать направление падающего пучка единичным вектором 
, а направление наблюдения - единичным вектором 
. Поскольку 
=1 и 
=1, то для углов , 
, 
, , 
, 
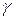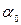, характеризующих направление падающего луча и направление, в котором проводится наблюдение, справедливы соотношения (рис.8):
 |
, 
(2).
 |
Тогда система уравнений (1) оказывается разрешимой относительно углов
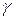, , только при определённых значениях длины волны 
. Условия (1) наблюдения максимума дифракционной картины называют условиями Лауэ.
Разделим каждое из трех уравнений системы (1) на длину соответствующего базисного вектора, возведем в квадрат и сложим. С учетом уравнений (2), получим:
(3).
Косинус угла между двумя прямыми может быть записан через косинусы углов между прямыми и осями координат. Обозначим угол между падающим пучком и направлением наблюдения через 
и перемножим скалярно единичные векторы, задающие направления пучков, выраженные через базис:
.
С учётом того, что 
и 
,
получим:
.
Тогда уравнение (3) можно переписать в виде:
или
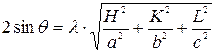. (4)
Для кубической решетки, когда 
, равенство упростится:
.
 |
Русский ученый Ю.В.Вульф и английские физики У.Г. и У.Л.Брэгги независимо друг от друга показали, что расчёт дифракционной картины от кристаллической решётки можно осуществить и более простым способом. Они предложили считать, что интерферируют лучи, отраженные от параллельных плоскостей, проведенных через узлы кристаллической решётки. В этом случае интерференционная картина рассчитывается подобно тому, как это делается для тонких плёнок. Разность хода между лучами, пришедшими в точку наблюдения от соседних плоскостей при наблюдении под тем же углом к плоскостям, что и угол между плоскостями и падающим пучком, может быть записана (рис.9):
.
 |
Следовательно, максимум дифракционной картины будет наблюдаться под таким углом скольжения 
(угол Брэгга), который удовлетворяет условиям Вульфа-Брэгга
.
Наблюдения в этом случае также проводятся под углом . Таким образом, угол между направлениями падающего луча и направлением, в котором наблюдается максимум дифракционной картины, будет равен двойному брэгговскому углу.
Расчет по формулам Лауэ дает те же самые направления. Сравнивая условия Вульфа-Брэгга с выведенным из условий Лауэ соотношением (4), можно получить связь межплоскостных расстояний 
с параметрами решётки a, b, c и индексами плоскостей (hkl):
В случае кубической решётки a=b=c и тогда
Поиск по сайту: