 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теоретические предпосылки работы
Как сказано было выше, дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле – любое отклонение при распространении волн от законов геометрической оптики.
Различают дифракцию Френеля и дифракцию Фраунгофера. Дифракция Френеля, или дифракция сферических волн, происходит в сферических световых волнах, когда дифракционная картина наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию.
Дифракция Фраунгофера наблюдается в параллельных лучах, получаемых при помощи оптических систем - коллиматоров. При использовании лазера оптическая система значительно упрощается, т.к. излучаемые световые пучки являются параллельными и не требуют применения оптические систем для их коллимации.
Схема наблюдения дифракции Фраунгофера от одной щели представлена на рисунке 7
. 
Рисунок 7 Схема наблюдения дифракции Фраунгофера от одной щели
Параллельный пучок от (Не – Nе)- лазера 1 падает нормально на щель 2, длина которой больше ее ширины b. Согласно принципу Гюйгенса, каждая течка плоскости щели, до которой дошло световое колебание, становится источником вторичных волн, распространяющихся во все стороны под углами дифракции j1, j2 …, т.е. свет дифрагирует при прохождении через цель. Дифрагированные пучки являются когерентными и могут интерферировать при наложении. Результат интерференции в виде периодического распределения интенсивности наблюдается на экране 3, находящимся на расстоянии 
от щели 2.
Распределение интенсивности в получаемой картине определяется суммированием элементарных волн, приведших в данную точку экрана от всех элементов щели, с учетом их амплитуды и фазы по принципу Гюйгенса-Френеля.
При небольшим углах дифракции наиболее просто рассчитать интенсивность графическим методом, предложенным Френелем. Для этого разобьем часть волнового фронта в плоскости щели на узкие полоски - зоны равной длины, параллельным краям щели. В данном случае волны в плоскости щели совпадает с волновой поверхностью, т.е. фаза во всех его точках одинакова. Каждая зона (полоска) будет играть элементарного вторичного источника волн. Колебание DA от каждой зоны имеет одинаковую амплитуду и отстает от предыдущего колебания на одну и ту же величину s, зависящую от угла дифракции j, определяющего направление на точку наблюдения Р. При разность фаз s равна нулю и векторная диаграмма имеет вид, показанный на рисунке 8
Рисунок 8 Векторная диаграмма распределения интенсивности при φ0=0
Амплитуда результирующего колебания А0 равна алгебраической сумме амплитуд складываемых колебаний. Если разность фаз складываемых колебаний, соответствующих краям щели, равна p (т.е. разность хода 
/2), товекторыDA располагаются вдоль полуокружности длиной А 0 (рисунок 9). Следовательно, для результирующей амплитуды получим значение 
= 2 
.
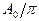Рисунок 9 Векторная диаграмма распределения интенсивности при φ0=π
В случае когда , колебания от краев щели отличаются по фазе на 2p.Соответствующая векторная диаграмма дана на рисунке 10.
Рисунок 10 Векторная диаграмма распределения интенсивности при φ0=2π
.Строя последовательно векторы, мы обойдем полтора раза окружность диаметра А1=2А0/(3p). (Рисунок 11). Таким образом, амплитуда А1 первого максимума составляет 2/(3p) от амплитуды А0 нулевого максимума, а интенсивность I1 = A 
.
В результате получаются следующие соотношения интенсивностей:
Рисунок 11 Векторная диаграмма распределения интенсивности при φ0=3π
Так как графический расчет является приближенным, то полученные соотношения также будут приближенными.
Т.о., центральный нулевой максимум значительно превосходит по интенсивности остальные максимумы. Ему соответствуют 90% всего светового потока, выходящего из щели. Нетрудно видеть, что нулевая амплитуда будет соответствовать углам дифракции jК, при которых:
(10)
где K=1, 2, 3, 4 —. порядок дифракционного минимума.
Следовательно (10) будет условием дифракционного минимума. при К=О, как видно; j= 0 и условие b×sinj0=- 0 будет условием центрального нулевого порядка.
Условие дифракционного максимума выражается по уточненным формулам:
(11)
График распределения интенсивности на экране 3 показан на рисунке 12
Рисунок 12 График распределения интенсивности света на экране
Наблюдаемость дифракционной картины Фраунгофера зависит от ширины щели, а также расстояния от щели до экрана 3. если,|например ширина щели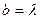 
, то 
следовательно, j1=p/2, т.е. ни одного дифракционного минимума наблюдаться не будет экран будет весь освещен,больше в середине и меньше к краям. Это соответствует чистой дифракции без интерференции. при малых углах дифракции картина может бать слишком мелкой для наблюдения.
В настоящей работе предлагается составить схему дифракции от щели, позволяющей отчетливо наблюдать дифракционную картину и построить распределения интенсивности.
Поиск по сайту: