РАСЧЕТ ПРОЧНОСТИ НОРМАЛЬНЫХ СЕЧЕНИЙ

Расчет прочности нормальных сечений

Рассмотрим для примера однопролетную железобетонную балку, свободно лежащую на двух опорах, симметрично загруженную двумя сосредоточенными силами. Участок балки между грузами находится в условиях чистого изгиба; в его пределах действует только изгибающий момент М, поперечная сила равна нулю.

Рис. 8.1. Схема изгибаемого железобетонного элемента

На определенной ступени загружения в бетоне растянутой зоны этого участка под воздействием растягивающих напряжений образуются нормальные трещины, т.е. трещины, направленные перпендикулярно продольной оси балки. На участках между опорой и грузом действует одновременно изгибающий момент М и поперечная сила Q. Здесь образуются наклонные трещины.

В сечениях, нормальных к продольной оси элементов – изгибаемых, внецентренно сжатых, внецентренно растянутых – при двузначной эпюре напряжений в стадии III характерно одно и то же НДС. В расчетах прочности элементов усилия, воспринимаемые сечением, нормальным к продольной оси элемента, определяют по расчетным сопротивлениям материалов с учетом коэффициентов условий работы.

Рис. 8.2. К расчету прочности сечений любой симметричной формы

В общем случае условие прочности при любом из перечисленных внешних воздействий формулируется в виде требования о том, что момент внешних сил не превосходил момента внутренних усилий.

(8.1)

(8.2)

где М – в изгибаемых элементах момент внешних сил от расчетных нагрузок;

статический момент площади сечения бетона сжатой зоны относительно той же оси;

статические моменты площадей напрягаемой и ненапрягаемой сжатой арматуры;

расстояние междуцентром тяжести бетона сжатой зоны и центром тяжести растянутой (напрягаемой и ненапрягаемой) арматуры.

расстояние междуцентром тяжести арматуры

ИЗГИБАЕМЫЕ ЭЛЕМЕНТЫ. РАСЧЕТ ПРОЧНОСТИ ПО НАКЛОННЫМ СЕЧЕНИЯМ

1. Основные расчетные положения

Образование наклонных трещин в изгибаемых элементах (особенно у опор балок) обусловлено совместным действием изгибающих моментов и поперечных сил, т.е. при изгибе железобетонного элемента возникают, кроме нормальных напряжений, скалывающие напряжения, действующие по горизонтальному и вертикальному направлениям.

Место их образования, наклон, раскрытие и развитие по высоте зависят от вида нагрузок, формы сечения, вида армирования и т.д.

Рис. 11.1. Схема действий напряжений в изгибаемой железобетонной балке

––––––– – нормальные трещины;

––––––– – наклонные трещины

В наклонных сечениях имеют место те же 3 стадии НДС, как и в нормальных сечениях.

После образования наклонной трещины изгибаемый элемент разделяется на две части, связанные между собой в сжатой зоне бетоном над наклонной трещиной, продольной арматурой, хомутами и отгибами, пересекающими наклонную трещину – в растянутой зоне

При увеличении нагрузки наклонная трещина раскрывается, и разрушение происходит по одному из трех возможных случаев.

Случай 1 – раздробление бетона стенки по наклонной полосе между наклонными трещинами от главных сжимающих напряжений.

Рис. 11.2. Схема разрушения изгибаемого элемента по наклонному сечению по сжатой полосе между наклонными трещинами

1 – наклонная трещина;

2 – раздробление сжатой полосы стенки

Такое разрушение возможно при малой ширине b сечения элемента (тавровое, двутавровое, коробчатое) в зоне действия поперечных сил, когда величина главных сжимающих напряжений 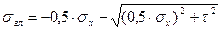может превзойти прочность бетона на сжатие . Это обусловлено возникновением в стенке двуосного напряженного состояния, при котором по взаимно перпендикулярным площадкам действуют сжимающие и растягивающие напряжения. Последние существенно снижают прочность на сжатие.

Случай 2 – сдвиг по наклонному сечению от доминирующего действия поперечной силы.

Образование наклонной трещины начинается в середине боковых граней, где касательные напряжения от поперечной силы достигают своего максимального значения , где – главные растягивающие напряжения на уровне нулевой линии элементов без напрягаемой арматуры.

Вследствие неупругих свойств бетона касательные напряжения распределяются равномерно по сечению, поэтому наклонная трещина раскрывается примерно одинаково по всей длине. При разрушении происходит взаимное смещение частей элемента по вертикали.

Если касательные напряжения не достигают своего максимального значения (т.е. ), то наклонной трещины не образуется.

Рис. 11.3. Схема разрушения изгибаемого элемента по наклонному сечению от доминирующего действия поперечной силы

1 – нулевая линия;

2 – наклонная трещина;

3 – хомуты

Случай 3 – излом по наклонному сечению от доминирующего действия изгибающего момента М.

Под воздействием постепенно возрастающего изгибающего момента главные растягивающие напряжения 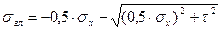преодолевают сопротивление бетона на осевое растяжение и образуется наклонная трещина с максимальным раскрытием в растянутой зоне. Бетон растянутой зоны из деформирования выключается и все растягивающие усилия передаются на продольную и поперечную арматуру. Происходит взаимный поворот частей элемента вокруг мгновенного центра вращения, расположенного в центре тяжести D сжатой зоны сечения.

Рис. 11.4. Схема разрушения изгибаемого элемента по наклонному сечению от доминирующего действия изгибающего момента

1 – нулевая линия;

2 – наклонная трещина;

3 – хомуты

Если главные растягивающие напряжения не достигают значения осевого сжатия, т.е. , то наклонной трещины не образуется и поперечная сила полностью воспринимается одним бетонным сечением.

Прочность элементов по наклонным сечениям на совместное действие изгибающего момента М и поперечной силы Q рассчитывают в зависимости от случая разрушения элементов.

Рис. 11.5. К расчету по наклонным сечениям

Исходя из описанной схемы излома элемента, разрушающий момент и разрушающая поперечная сила в наклонном сечении равны:

– сумма проекций внутренних усилий на нормаль к оси элемента.

– сумма моментов внутренних усилий относительно точки приложения равнодействующей сжатой зоны на нормаль к оси элемента.

где площади сечений соответственно поперечной арматуры (хомутов), наклонной арматуры (отгибов), продольной (рабочей) арматуры;

расстояния до точки D соответственно от хомутов, отгибов и продольной арматуры.

Поиск по сайту: