Теория асимметричной информации

Асимметричная информация имеет место, когда менеджер знает о будущем своего предприятия больше, чем наблюдающие за ней аналитики и инвесторы. В этом случае менеджеры могут на основе имеющейся у них закрытой информации определить, что цена акций или облигаций их предприятия завышена или занижена. Существуют различные степени асимметрии, так как руководство предприятия всегда лучше, чем посторонние наблюдатели, информировано о его перспективах. Однако нередко эта разница в информированности часто слишком мала, чтобы оказать влияние на действия менеджеров. Сигнализация. Асимметричная информация может оказывать значительное влияние и на финансовые рынки, и на решения, принимаемые менеджерами. Для того чтобы обеспечить высокую котировку акций, предприятия, менеджеры должны информировать рынок о скрытом от него потенциале предприятия. Такие действия называют сигналами, а процесс передачи сигналов — сигнализацией.

Простейший способ подачи сигналов — это проведение пресс-конференции и заявление с благоприятной информацией. Но эти акции малоэффективны. Классическим эффективным примером распространения информации в форме сигнализации являются объявления о значительном увеличении выплачиваемых дивидендов. Когда же большинство инвесторов ожидают увеличения дивидендов, а этого не происходит, менеджеры дают негативный сигнал.

7. Оценка общего риска: ожидаемая доходность, среднеквадратическое отклонение, коэффициент вариации по отдельной ценной бумаге

1)

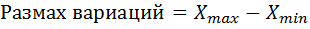
2) Дисперсия () = средний квадрат отклонений от значений средней

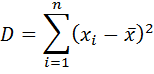
3) Среднеквадратическое отклонение

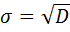
4) Коэффициент вариации

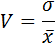
Для расчёта показателей финансовой активности:

Наиболее вероятная доходность

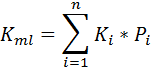
– прогнозная доходность для каждого вида

– вероятность реализации этой доходности

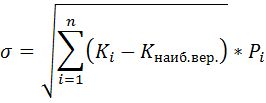
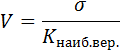
8. Оценка рыночного риска: доходность портфеля, коэффициент корреляции между активами и риск портфеля, среднеквадратическое отклонение по портфелю ценных бумаг

Оценка рыночного риска доходность портфеля, коэффициент корреляции между активами и риск портфеля, среднеквадратическое отклонение по портфелю ценных бумаг.

Ожидаемая доходность портфеля — набора активов представляет собой взвешенную среднюю из показателей ожидаемой доходности отдельных активов, входящих в

данный портфель:

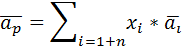
где ар — ожидаемая доходность портфеля;

xi — доля стоимости портфеля, инвестированная в i-й актив;

aj — ожидаемая доходность i-го актива;

i — порядковый номер актива,

n — число активов в портфеле;

Риск портфеля в большинстве случаев меньше риска входящих в его состав активов. Для измерения риска портфеля необходимо вычислять среднее квадратическое отклонение его доходности. При дискретном распределении доходности его легко может подсчитать, определив дисперсию доходности портфеля следующим образом:

где дисперсия доходности портфеля;

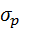— среднее квадратическое отклонение доходности портфеля;

— ожидаемая доходность портфеля;

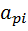-ожидаемая доходность портфеля при i-м состоянии экономики;

- вероятность i-го состояния экономики;

m — число возможных состояний экономики.

Ковариация и коэффициент корреляции являются основными понятиями, используемыми для анализа риска портфеля. Напомним, ковариация — это мера, учитывающая дисперсию, или разброс индивидуальных значений доходности акции либо других активов, и силу связи между изменением доходности данной акции и других акций.

Например, ковариация между акциями А и В показывает, существует ли взаимосвязь между увеличением или уменьшением значения доходности этих акций, а кроме того,

силу этой взаимосвязи. Ковариация рассчитывается так:

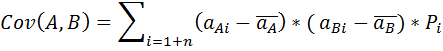
где

— ковариация доходности акций А относительно доходности акций В;

— ожидаемая доходность акций А;

— ожидаемая доходность акций А при i-м состоянии экономики;

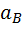— ожидаемая доходность акций В;

— ожидаемая доходность акций В при i-м состоянии экономики;

— вероятность i-го состояния экономики; n — число возможных состояний экономики.

Содержательно интерпретировать численное значение ковариации довольно сложно, поэтому для измерения силы связи между двумя переменными используется другая

статистическая характеристика, называемая коэффициентом корреляции. Напомним, что корреляцией называется тенденция двух переменных к совместному изменению. Сила этой тенденции и измеряется с помощью коэффициента, который лежит в пределах от +1,0 (что означает тождественное изменение переменных) до —1,0 (что означает изменение значений двух переменных абсолютно противоположным образом). Равенство коэффициента корреляции нулю указывает отсутствие связи между переменными.

Коэффициент корреляции между переменными A и В рассчитывается следующим образом:

где

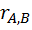— коэффициент корреляции между доходностью акций А и В;

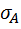— среднее квадратическое отклонение доходности акций А;

— среднее квадратическое отклонение доходности акций В.

9. Оценка рыночного риска: ковариация и коэффициент корреляции, среднеквадратическое отклонение портфеля, состоящего из двух ценных бумаг

Портфель, состоящий из нескольких активов. Если

распределения доходности отдельных ценных бумаг являются

нормальными, то для определения риска портфеля,

состоящего из нескольких активов, используют следующую

формулу:

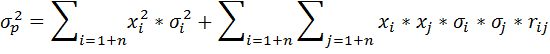
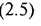
где

—дисперсия доходности портфеля;

среднее квадратическое отклонение доходности портфеля;

x_i и x_j — доли i-го и j-го активов в портфеле;

и — средние квадратические отклонения доходности i-го и j-го активов;

n — число возможных состояний экономики;

значками и обозначено суммирование по всем n

активам, причем во втором слагаемом i ≠ j;

, — коэффициент корреляции между доходностью актива i и актива j

В случае двух активов в портфеле формула (2.5) примет

следующий вид:

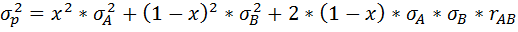
11. Модель CAMP: построение линии CML, уравнение CML

12. Модель CAMP: уравнение SML, линия SML

13. Модель CAMP: влияние инфляции, отношения инвестора к риску на SML

Основные положения модели оценки доходности финансовых активов (Capital Asset Pricing Model — САРМ):

1) цель инвесторов — максимизация возможного прироста своего достояния на конец планируемого периода путем оценки ожидаемой доходности и средних квадратических отклонений альтернативных инвестиционных портфелей;

2) инвесторы могут брать и давать без ограничения ссуды по некоей,безрисковой процентной ставке aRF;

3) инвесторы одинаково оценивают величину ожидаемых значений дисперсии и ковариации доходности активов;

4) все активы абсолютно делимы и совершенно ликвидны — всегда могут быть проданы на рынке по существующей цене;

5) не существует трансакционных издержек;

6) налогов нет;

7) инвесторы, предполагая, что их деятельность влияет на уровень цен, принимают цену как заданную величину;

8) количество финансовых активов заранее определено и фиксировано.

Линия рынка капитала (CML) — это линия RMZ на рис. 2.2, построенном в координатах «риск — доходность». Она пересекается с вертикальной осью в точке, соответствующей доходности aRF.

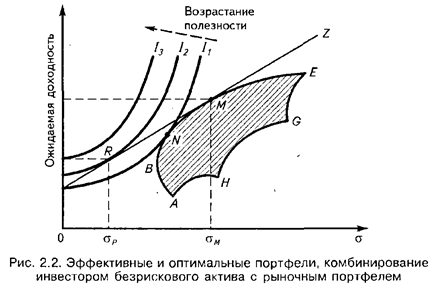
На рис. 2.2 -точка N, в которой кривая безразличия Ii касается границы эффективного множества, отражает выбор оптимального портфеля рисковых активов, который обеспечивает инвестору самую высокую доходность при данной величине риска σN. Но инвестор может сделать лучший выбор, чем портфель N. Он может достичь более высокой кривой безразличия, если в дополнение к возможному множеству рисковых портфелей можно воспользоваться безрисковым активом, который обеспечивает

гарантированную доходность aRF. На оси доходности это — величина, из которой исходит линия рынка капитала RMZ.

Инвестор может составить новые портфели путем включения в свой портфель безрискового актива. Это позволяет достичь комбинации риска и доходности на прямой

линии рынка капитала. Используя новую возможность, ин-вестор перейдет из точки N в точку R, которая находится на более высокой кривой безразличия «риск—доходность».

Все инвесторы при условии соблюдения предпосылок САРМ должны иметь портфели, являющиеся комбинацией безрисковой ценной бумаги и рискового портфеля М.

Уравнение линии рынка RMZ:

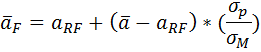
Уравнение показывает, что доходность эффективного -портфеля равна сумме безрисковой ставки aRF и премии за риск. Наклон линии рынка капитала CML определяется выражением

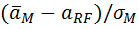
Линия рынка ценных бумаг. В теории САРМ рисковость ценной бумаги измеряется ее β-коэффициентом (бета-коэффициентом). Этот, коэффициент характеризует изменчивость доходности конкретной акции относительно доходности рынка ценных бумаг. По определению некая «средняя» акция имеет р, равный 1,0; акция, изменчивость доходности которой выше, чем в среднем на рынке, имеет C > 1,0; акция, изменчивость доходности которой меньше, чем в среднем на рынке, имеет В < 1,0. Уравнение связи между риском акции и доходностью акции называется уравнением линии рынка ценных бумаг (SML):

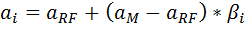
где

— требуемая доходность i-й акции;
— безрисковая доходность, в качестве которой на многих фондовых рынках принимается доходность облигаций казначейства США;

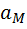— требуемая доходность рыночного портфеля, состоящего из всех акций.

Влияние инфляции. Оно сказывается в теории САРМ на доходности всех активов одинаково, поэтому линия рынка ценных бумаг поднимается по шкале ставок доходности

на величину инфляционной премии. Изменение отношения к риску. Крутизна линии рынка ценных бумаг отражает отношение инвесторов к риску: чем круче наклон линии, тем в большей степени они пытаются элиминировать риск.

14. Концепция β – коэффициента

Показатели средней акции по определению должны варьировать в соответствии с изменениями ситуации на рынках, измеряемыми биржевыми индексами, примером

которых может служить известный индекс Нью-Йоркской фондовой биржи. Средняя акция имеет р-коэффициент, равный 1,0. Это значит, что, например, при изменении

ситуации на рынке вверх или вниз на один процентный пункт характеристики акции. меняются в том же направлении на один процентный пункт. Доходность портфеля из акций с C = 1,0 будет повышаться или понижаться одновременно с изменением среднего рыночного курса, а риск портфеля будет совпадать со средним на рынке. Если акция имеет C = 0,5, ее характеристики будут меняться в 2 раза медленнее, чем в среднем на рынке. Портфель, состоящий из таких акций, будет иметь риск, равный половине 2,0, то изменчивость характеристик акции в 2 раза выше по сравнению со средней акцией, поэтому портфель, состоящий из таких акций, в 2 раза рисковее среднего портфеля.

Бета-коэффициенты подсчитываются и публикуются, представляются на сайтах в Интернете биржевыми агентствами.

Бета-коэффициент портфеля ценных бумаг (βр) рассчитывается по формуле средней арифметической взвешенной:

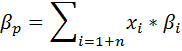
где xi и βi — доля и бета-коэффициент i-й ценной бумаги в портфеле; n — число ценных бумаг в портфеле. Добавление в портфель акции, имеющей β > 1, увеличивает значение β и повышает рисковость портфеля, и наоборот.
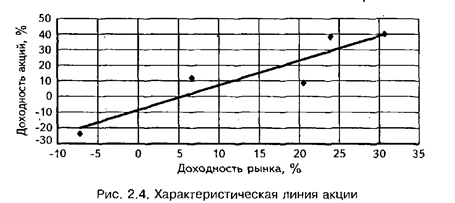
Характеристическая линия и расчет бета-коэффициентов. Уильям Шарп, разрабатывая теорию САРМ, показал, что рыночный риск любой акции может быть оценен на основе анализа тенденций изменения ее характеристик по отношению к среднерыночным их значениям.

Величина фактической доходности конкретной акции и величина доходности на рынке акций в среднем по календарным периодам оказываются взаимосвязаны. Эта взаимосвязь выражается линейной регрессионной зависимостью вида:

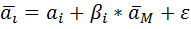
где ai— доходность i-й акции; аM — доходность рынка в среднем; αi и βi — коэффициенты уравнения регрессии; ε — случайная ошибка.

Параметры уравнений регрессии по данным о доходности акции и рынка за календарные периоды могут быть просчитаны с помощью средств анализа данных, имеющихся в электронных офисах на персональных компьютерах.

15. Понятия цены и стоимости финансового актива. Теории оценки финансовых активов

Любой вид товара имеет множество характеристик: цена, степень соответствия моде, потребительские качества, наличие потенциальной способности приносить доход владельцу и др. Финансовый актив, являясь в принципе обычным товаром на рынке капитала, также может быть охарактеризован с различных позиций. Этот товар имеет меньшее количество характеристик по сравнению с потребительскими товарами, в частности, в этой главе внимание будет сконцентрировано на трех основных характеристиках: цене, стоимости и доходности; в следующей главе мы рассмотрим еще одну чрезвычайно важную характеристику финансового актива -- риск.

Что касается первых трех показателей, то их существенность определяется тем, что любой инвестор, принимая решение, например, о целесообразности приобретения того или иного финансового актива, пытается оценить экономическую эффективность планируемой операции. Совершенно очевидно, что он может при этом ориентироваться либо на абсолютные, либо на относительные показатели. В первом случае речь может идти о цене и/или стоимости актива, во втором -- о его доходности.

Логика рассуждений инвестора, например, в первом случае такова. Финансовый актив имеет две взаимосвязанные абсолютные характеристики: во-первых, объявленную текущую рыночную цену (Рm), по которой его можно приобрести на рынке, и, во-вторых, теоретическую, или внутреннюю, стоимость (Vt,). Разница между этими характеристиками достаточно очевидна даже на житейском уровне. Так, для любого коллекционера некоторая вещица, найденная нм на рынке и относящаяся к сфере его интересов, может быть практически бесценной, тогда как для человека, не интересующегося этим, она не стоит и ломаного гроша.

Очевидно, что обе абсолютные характеристики не только меняются в динамике, но с позиции конкретного инвестора нередко могут не совпадать. По сравнению с ценой, которая реально существует и объективна, по крайней мере, в том смысле, что она объявлена и товар по ней равнодоступен любому участнику рынка, внутренняя стоимость гораздо более неопределенна и субъективна. Под субъективностью в данном случае понимается то обстоятельство, что каждый инвестор имеет свой взгляд на внутреннюю стоимость актива, полагаясь в ее оценке на результаты собственного, т.е. субъективного, анализа. Возможны три ситуации:

Первое соотношение свидетельствует о том, что с позиции конкретного инвестора данный актив продается в настоящий момент времени по завышенной цене, поэтому инвестору нет смысла приобретать его на рынке, Второе соотношение говорит об обратном: цена актива занижена, есть смысл его купить. Согласно третьему соотношению текущая цена полностью отражает внутреннюю стоимость актива, поэтому спекулятивные операции по его скупке/продаже вряд ли целесообразны. Таким образом, если в каждый момент времени рыночная цена конкретного актива существует в единственном числе, то внутренняя его стоимость множественна; в принципе каждый финансовый актив имеет столько оценок значений этого показателя, сколько имеется инвесторов на рынке, заинтересованных в данном активе.

Итак, можно сформулировать несколько условных правил, позволяющих провести определенное различие между ценой и стоимостью финансового актива:

* стоимость -- расчетный показатель, а цена -- декларированный, т.е. объявленный, который можно видеть в прейскурантах, ценниках, котировках;

* в любой конкретный момент времени цена однозначна, а стоимость многозначна, при этом число оценок стоимости зависит от числа профессиональных участников рынка;

* с известной долей условности можно утверждать, что стоимость первична, а цена вторична, поскольку в условиях равновесного рынка цена, во-первых, количественно выражает внутренне присущую активу стоимость и, во-вторых, стихийно устанавливается как среднее из оценок стоимости, рассчитываемых инвесторами.

Приведенная аргументация будет использоваться нами и в некоторых последующих разделах книги.

Каким же образом рассчитывается внутренняя стоимость финансового актива, имеющего в некоторый момент времени to текущую цену Pm? В зависимости от того, что является методологическим и информационным обеспечением процесса оценивания, существуют три основные теории оценки: фундаменталистская, технократическая и теория ходьбы наугад» (рис. 1).

Рис. 1. Подходы к оценке финансовых активов

Фундаменталисты считают, что любая ценная бумага имеет внутренне присущую ей ценность, которая может быть количественно оценена как дисконтированная стоимость будущих поступлений, генерируемых этой бумагой, т.е. нужно двигаться от будущего к настоящему. Все дело лишь в том, насколько точно удается предсказать поступления, а это можно сделать, анализируя общую ситуацию на рынке, инвестиционную н дивидендную политику компании, инвестиционные возможности н т.п. Данный подход к анализу на фондовом рынке известен как фундаментальный анализ.

Технократы, напротив, предлагают двигаться от прошлого к настоящему и утверждают, что для определения текущей внутренней стоимости конкретной ценной бумаги достаточно знать лишь динамику ее цены в прошлом. Используя статистику цен, а также данные о котировках цен и объемах торгов, они предлагают строить различные долго- средне- и краткосрочные тренды и на их основе определять, соответствует ли текущая цена актива его внутренней стоимости. В систематизированном виде эти подходы изложены в рамках так называемого технического анализа.

Последователи теории «ходьбы наугад» считают, что текущие цены финансовых активов гибко отражают всю релевантную информацию, в том числе и относительно будущего ценных бумаг. Они исходят из предположения, что текущая цена всегда вбирает в себя всю необходимую информацию, которую, следовательно, и не нужно искать дополнительно. Точно так же и все будущие ожидания концентрированно отражаются в текущей цене. Поскольку новая информация с одинаковой степенью вероятности может быть как «хорошей», так и «плохой», невозможно с большей или меньшей определенностью предсказать изменение цены в будущем, т.е. внутренняя 'стоимость, равно как и цена конкретного финансового актива, меняется совершенно непредсказуемо и не зависит от предыдущей динамики. Таким образом, любая информация то ли статистического, то ли прогнозного характера не может привести к получению обоснованной оценки.

Можно сказать, что фундаменталистская теория является наиболее распространенной. Согласно этой теории текущая внутренняя стоимость (Vt,) любой ценной бумаги в общем виде может быть рассчитана по формуле:

где CF, -- ожидаемый денежный поток в i-м периоде (обычно год);

r -- приемлемая (ожидаемая или требуемая) доходность.

Таким образом, подставляя в эту формулу значения предполагаемых поступлений, доходности и продолжительности периода прогнозирования, можно рассчитать текущую внутреннюю стоимость любого финансового актива. Именно такой подход чаще всего и используется потенциальными инвесторами.

Необходимо особо обратить внимание на то, что в алгоритмах оценки, базирующихся на этой и подобных формулах, негласно подразумевается капитализация получаемых доходов (проценты, дивиденды) с доходностью, равной ставке дисконтирования из формулы оценки. Например, в случае с облигацией ее оценка, полученная с помощью формулы, будет верна только в том случае, если регулярно получаемые проценты не используются для потребления, а немедленно инвестируются в те же самые облигации или в ценные бумаги с той же доходностью и степенью риска. В том случае, если возможность такого инвестирования отсутствует или не планируется, применение формулы является ошибкой.

Итак, рыночная цена, как характеристика ценности актива, является величиной относительной. В частности, на вторичном рынке значение этого показателя устанавливается как среднее ожидаемых цен потенциальных инвесторов. Несмотря на складывающуюся на рынке вполне определенную текущую цену, любой финансовый актив может иметь различную степень привлекательности для потенциальных инвесторов и в этом смысле может иметь для них различную ценность. Причин тому может быть несколько: различная оценка возможных денежных поступлений и приемлемой нормы прибыли, различные приоритеты в степени надежности и доходности и др.

Как видно из формулы, оценка теоретической стоимости зависит от трех параметров: ожидаемые денежные поступления, горизонт прогнозирования и норма прибыли. В отношении первого параметра существуют различные подходы и модели, которые будут изложены ниже. В отношении второго параметра модели варьируют в зависимости от того, что представляет собой базисный актив: для облигаций и привилегированных акций горизонт прогнозирования чаще всего ограничен, для обыкновенных акций он обычно равен бесконечности. Последний параметр, вероятно, наиболее существен. Первые два параметра тесно привязаны непосредственно к базисному активу и потому обладают большей степенью объективности. Приемлемая норма прибыли, закладываемая инвестором в анализ, в этом случае в принципе не имеет отношения к базисному активу -- она лишь отражает доходность альтернативных вариантов вложения капитала, доступных, возможно, лишь данному инвестору, что и предопределяет вариабельность этого параметра. Вот почему именно нормой прибыли обычно варьируют инвесторы в процессе имитационного моделирования. В частности, приемлемая норма прибыли может устанавливаться инвестором следующими способами:

* в размере процентной ставки по банковским депозитам (rb);

* исходя из процента, выплачиваемого банком вкладчику за хранение его средств (rb), и надбавки за риск инвестирования в данный финансовый актив (rr):

* исходя из процента, выплачиваемого по правительственным облигациям (rsb), и надбавки за риск (rr):

Именно ввиду различия в оценках базовых показателей рынок ценных бумаг существует. Оценивая текущую внутреннюю стоимость ценной бумаги, инвестор, в частности, варьирует значениями нормы прибыли н ожидаемых поступлений, которые могут значительно отличаться у различных инвесторов.

16. Оценка облигаций с нулевым купоном и их доходности. Оценка бессрочных облигаций

В отличие от купонных, данный вид облигаций не предусматривает периодических выплат процентов. Поскольку доход по ним образуется в виде разницы между ценой покупки и ценой погашения, бескупонные облигации размещаются на рынках только со скидкой (с дисконтом). Соответственно рыночная цена такой облигации всегда ниже номинала. Иногда бескупонные облигации называют также дисконтными.

Следует отметить, что отечественный рынок бескупонных облигаций представлен, в основном, краткосрочными государственными (ГКО), республиканскими (РКО), областными (ОКО) и муниципальными (МКО) ценными бумагами, методы анализа которых будут рассмотрены в следующей главе. Долгосрочные бескупонные облигации на момент написания данной работы на фондовых рынках России отсутствовали.

Тем не менее, этот вид долгосрочных обязательств достаточно перспективен и пользуется большой популярностью у инвесторов в развитых странах, поскольку он не несет риска, связанного с реинвестированием периодических доходов в условиях колебаний процентных ставок на рынке. Кроме того, часто держатели этих бумаг получают определенные налоговые преимущества. Рассмотрим технику оценки долгосрочных бескупонных облигаций.

Доходность долгосрочных бескупонных облигаций

Поскольку единственным источником дохода здесь является разница между ценой покупки и номиналом (ценой погашения), проведение операций с бескупонными облигациями порождают элементарный поток платежей. В данном случае подобный поток характеризуется следующими параметрами: ценой покупки P (современная стоимость облигации), номиналом N (будущая стоимость), процентной ставкой r (норма доходности) и сроком погашения облигации n. Напомним, что любой параметр операции с элементарным потоком платежей может быть найден по известным значениях трех остальных (см. главу 1). Однако поскольку номинал облигации всегда известен (или может быть принят за 100%), для определения доходности операции достаточно знать две величины – цену покупки P (либо курс К) и срок погашения n.

Тогда доходность к погашению бескупонной облигации можно определить по следующей формуле:

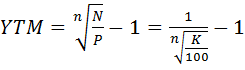(2.17)

Из (2.17) следует, что доходность бескупонной облигации YTM находится в обратной зависимости по отношению к цене P и сроку погашения n.

Оценка стоимости бескупонных облигаций

Процесс оценки стоимости бескупонной облигации заключается в определении современной величины элементарного потока платежей, по известным значениям номинала N, процентной ставки r и срока погашения n. Пусть r = YTM. С учетом принятых обозначений, формула текущей стоимости (цены) подобного обязательства примет следующий вид:

(2.18)

Поскольку номинал бескупонной облигации принимается за 100%, ее курсовая стоимость равна:

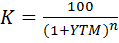(2.19)

Из приведенных соотношений следует, что цена бескупонной облигации связана обратной зависимостью с рыночной ставкой r и сроком погашения n. При этом чем больше срок погашения облигации, тем более чувствительней ее цена к изменениям процентных ставок на рынке.

Дюрация бескупонной облигации всегда равна сроку погашения, т.е.: D = n.

Облигации с нулевым купоном представляют интерес для инвесторов, проводящих операции с четко определенным временным горизонтом.

Поиск по сайту: