Комбинированные модели наращения и дисконтирования

Логика построения основных алгоритмов проста и основана на следующей идее. Простейшим видом финансовой сделки является однократное предоставление в долг некоторой суммы PV с условием, что через некоторое время t будет возвращена большая сумма FV. Как известно, результативность подобной сделки может быть охарактеризована двояко: либо с помощью абсолютного показателя — прироста (FV — PV), либо путем расчета некоторого относительного показателя. Абсолютные показатели чаще всего не подходят для подобной оценки ввиду их несопоставимости в пространственно-временном аспекте. Поэтому пользуются специальным коэффициентом — ставкой. Этот показатель рассчитывается отношением приращения исходной суммы к базовой величине, в качестве которой, очевидно, можно взять либо PV, либо FV. Таким образом, ставка рассчитывается по одной из двух формул:

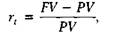
В финансовых вычислениях первый показатель имеет следующие названия: «процентная ставка», «процент», «рост», «ставка процента», «норма прибыли», «доходность», а второй — «учетная ставка», «дисконтная ставка», «дисконт».

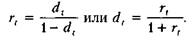
Оба показателя могут выражаться либо в долях единицы, либо в процентах. Различие в этих формулах состоит в том, какая величина берется за базу сравнения: в формуле (6.1) — исходная сумма, в формуле (6.2) — возвращаемая сумма.

Как же соотносятся между собой эти показатели? Очевидно, что rt > dt, а степень расхождения зависит от уровня процентных ставок, имеющих место в конкретный момент времени. Так, если rt = 8%, dt = 7,4%, т.е. расхождение сравнительно невелико; если г, = 80%, то dt = 44,4%, т. е. ставки существенно различаются по величине.

В прогнозных расчетах, например, при оценке инвестиционных проектов, как правило, имеют дело с процентной ставкой, хотя обычно это не оговаривается. Объяснение этому может быть таким. Во-первых, анализ инвестиционных проектов, основанный на формализованных алгоритмах, может выполняться лишь в относительно стабильной экономике, когда уровни процентных ставок невелики и сравнительно предсказуемы — в том смысле, что их значения не могут измениться в несколько раз или на порядок, как это имело место в России в переходный период от централизованно планируемой экономики к рыночной экономике. Если вероятна значительная вариабельность процентных ставок, должны применяться другие методы анализа и принятия решений, основанные, главным образом, на неформализованных критериях. При разумных значениях ставок расхождения между процентной и дисконтной ставками, как мы видели, относительно невелики, и потому в прогнозных расчетах вполне может быть использована любая из них. Во-вторых, прогнозные расчеты не требуют повышенной точности, поскольку результатами таких расчетов являются ориентиры, а не точные оценки. Поэтому, исходя из логики подобных расчетов, предполагающих их многовариантность, а также использование вероятностных оценок и имитационных моделей, излишняя точность не требуется.

Следует обратить внимание читателя на следующее весьма важное обстоятельство. В формулах (6.1) и (6.2) пока не акцентируется внимание на продолжительности периода, однако из алгоритма расчета с очевидностью следует, что обе ставки являются функцией времени: чем длительнее период, тем существеннее должно быть различие между суммовыми величинами PV и FV, а потому с изменением продолжительности временного интервала, т. е. продолжительности финансовой операции, должна меняться и ставка. Поскольку финансовые операции могут длиться от нескольких дней до нескольких лет, необходимо всегда помнить следующее правило: процентная ставка в финансовой операции должна быть некоторым образом увязана с продолжительностью операции. Обычно это делается путем задания некоторого базисного интервала, к которому привязывается ставка (год, квартал, месяц, день). Чаше всего характеристика финансовой операции делается с помощью годовой процентной ставки.

Процесс, в котором заданы исходная сумма и ставка (процентная или учетная), в финансовых вычислениях называется наращением, искомая величина — наращенной суммой, а используемая в операции ставка — ставкой наращения. Процесс, в котором заданы ожидаемая в будущем к получению (возвращаемая) сумма и ставка, называется дисконтированием, искомая величина — дисконтированной суммой (иногда используется термин приведенная сумма), а используемая в операции ставка — ставкой дисконтирования. В первом случае речь идет о движении денежного потока от настоящего к будущему, во втором — о движении от будущего к настоящем.

Поиск по сайту: