АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задача 20

Читайте также:
  1. I. 3.1. Двойственная задача линейного программирования
  2. II.2. Задача о назначениях
  3. II.4. МЕТОД ВЕТВЕЙ И ГРАНИЦ В ЗАДАЧАХ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ
  4. VI. Общая задача чистого разума
  5. В задачах 13.1-13.20 даны выборки из некоторых генеральных совокупностей. Требуется для рассматриваемого признака
  6. в задачах экспертного выбора.
  7. В) Задача
  8. В) Задача
  9. В) Задача
  10. В) Задача
  11. В) Задача
  12. В) Задача

Функция полезности индивидуума имеет вид: U(X,Y) = X*Y, где X и Y – количество благ X и Y. Доход индивидуума равен 180 ден. ед., а цены товаров Х и Y равны, соответственно, 8 и 18 ден. ед.
а) Определить оптимальную для индивидуума структуру покупок X и Y, при которой он достигает максимума полезности.


, где I – доход потребителя

 

 


 

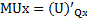
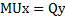
Qx = 11,25

Qy = 5

 

в) Сколько индивидуум будет потреблять блага X, если цена его сократится до 4 ден. ед., а цена блага Y не изменится?

 

Воспользуемся системой, которую вывели для задания а)

 


 

Qx = 22,5

Qy = 5

 


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)