АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Определение необходимого объема повторной и бесповторной выборок при оценке генеральной средней и доли

Читайте также:
  1. A) Определение массы тела по растяжению пружины
  2. A)нахождение средней из двух соседних средних, для отнесения полученного результата к определенной дате
  3. Access. Базы данных. Определение ключей и составление запросов.
  4. c) Определение массы тела по зависимости момента инерции системы, совершающей крутильные колебания от квадрата расстояния тела до оси вращения
  5. I. Дифракция Фраунгофера на одной щели и определение ширины щели.
  6. I. Иммунология. Определение, задачи, методы. История развитии иммунологии.
  7. I. Определение
  8. I. Определение
  9. I. Определение основной и дополнительной зарплаты работников ведется с учетом рабочих, предусмотренных технологической картой.
  10. I. Определение пероксида водорода (перекиси водорода)
  11. I. Определение проблемы и целей исследования
  12. I. Определение ранга матрицы

Формула доверительной вероятности при оценке генеральной доли признака. Средняя квадратическая ошибка повторной и бесповторной выборок и построение доверительного интервала для генеральной доли признака.

. теорема: вероятность того, что отклонение выборочной средней (или доли) от генеральной средней (или доли) не превзойдет число ∆>0, равна: Р(|ω-р|≤∆)=Ф(t)=γ, где t=∆/σω. это формула доверительной вероятности для доли. Среднее квадратическое отклонение выборочной средней и выборочной доли собственно-случайной выборки называется средней квадратической ошибкой. а)повторная выборка: σω=√pq/n ≈√ω(1-ω) /n (все под корнем и все делится на n). б) бесповторная выборка: σ ́΄ω=√ω(1-ω) / n * (1-n/N)(все под корнем). Построение доверительного интервала. Для построения доверительных интервалов для параметров генеральных совокупностей могут быть реализованы два подхода, основанных на знании точного(при данном объеме выборки n) или асимптотического (при n→∞) распределения выборочных характеристик. Первый подход реализован далее при построении интервальных оценок параметров для малых выборок.

2-ой вариант ответа Вер-ть того что отклонение выборочной доли по абсолютной величине не превзойдет числа ,равна

Где F-функция Лапласа, w-ген.доля p

Этот результат основывается на централ.пред.теор. В формуле D(w)есть неизв.пер. поэтому пользуемся приближ ф-ми. Сред.квад.ошибка

Доверит.интревал для доверит.доли может быть постр.по:

 

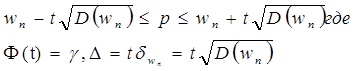
41 Формула доверительной вероятности при оценке генеральной средней. Средняя квадратическая ошибка повторной и бесповторной выборок и построение доверительного интервала для генеральной средней.

теорема: вероятность того, что отклонение выборочной средней (или доли) от генеральной средней (или доли) не превзойдет число ∆>0, равна: Р(|хвыб-х0|≤∆)=Ф(t)=γ, где t=∆/σх. это формула доверительной вероятности для средней. Среднее квадратическое отклонение выборочной средней и выборочной доли собственно-случайной выборки называется средней квадратической ошибкой. а)повторная выборка: σхвыб=√σ2/n≈√S2/n. б) бесповторная выборка: σ ́΄хвыб́=√S2/n(1-n/N)(все под корнем). Построение доверительного интервала. Для построения доверительных интервалов для параметров генеральных совокупностей могут быть реализованы два подхода, основанных на знании точного(при данном объеме выборки n) или асимптотического (при n→∞) распределения выборочных характеристик. Первый подход реализован далее при построении интервальных оценок параметров для малых выборок.

2-ой вариант ответа Вер-ть того что отклон. ген. сред. от a не привзойдёт по апсол.вел.числа где Ф-лап.

Это резул.следств.цен..пред.т.

В формуле есть неизв. перем.,поэтому пользуются приближ. Сред.квад.ош.:

Доверит.интревал.надёжности γ для ген.сред.может быть найден:

 

Определение необходимого объема повторной и бесповторной выборок при оценке генеральной средней и доли.

Для опред.n необход.задать надёжность оценки γ(дов.вер-ть) и точность Δ(пред.ош. выборки).

Для повтор.выб.при оценке ген. Сред.с надёжностью γ фор-ла для нах.объёма выборки имеет вид:

Где

Для беспов.

При оценке ген.доли для пов.выб.

Беспов.

Если найден объём повтор выб. n то объём соответствующей беспов. по фор-ле:

2ой вариант ответа для проведения выборочного наблюдения весьма важно правильно установить объем выборки n, который в значительной степени определяет необходимые при этом временные, трудовые и стоимостные затраты. Для определения n необходимо задать надежность (доверительную вероятность) оценки γ и точность (предельную ошибку выборки) ∆. 1. Для генеральной средней: а)повторная: n=t2*σ2 /∆2,б)бесповторная: n΄=N*t2*σ2 / t2*σ2 +N*∆2. для для генеральной доли: а) повторная: n=t2pq /∆2, б) бесповторная: n΄=N*t2pq / (t2pq + N∆2). Если найден объем повторной выборки n, то объем соответствующей бесповторной выборки n΄ можно определить по формуле: n΄= n*N /(n+N). Так как N /(n+N)<1, то при одних и тех же точности и надежности оценок объем бесповторной выборки n΄ всегда меньше объема повторной выборки n. на практике используется, в основном, бесповторная выборка.


Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)