Логические функции. Основные понятия и определения

Тема 17

Логические элементы

Основные понятия и определения

Логические элементы относятся к элементам дискретного действия, характеризующихся двумя устойчивыми состояниями. Переход от одного состояния в другое происходит скачком. Сигналы на выходе логического элемента имеют место лишь при определенном сочетании сигналов на входе.

Зависимость выходного сигнала от сочетания входных называется логической функцией.

Для математического описания логических функций и операций существует специальная алгебра логики (алгебра Буля) – это алгебра состояний, а не алгебра числа, а символы нельзя рассматривать как арифметические числа.

Алгебра логики – это формальный аппарат описания логической стороны процессов в цифровых устройствах.

Она имеет дело с логическими переменами, которых могут принимать только два значения 1 и 0. Эти два значения нельзя трактовать как числа, производить над ними арифметические действия. Это просто короткая удобная форма обозначения понятий ДА и НЕТ.

Логические переменные хорошо описывают состояния таких объектов, как реле, тумблеры. Кнопки, т.е. объектов, которые могут находиться в двух четко различных состояниях: включено – выключено. К этим объектам относятся и полупроводниковые логические элементы, на выходе которых может быть лишь один из двух четко различных уровней напряжения. Высокий уровень применяется за логическую единицу, а более низкий – за логический нуль.

Функции алгебры логики принимают значения 1 или 0 в зависимости от значения своих аргументов. Если это функция нескольких аргументов, то аргументы образуют некоторое множество комбинаций своих возможных значений.

Каждый логический элемент, имеющий один выход, выполняет определенную логическую функцию. В случае нескольких выходов число функций, выполняемых элементом, равно числу выходов.

Логические функции задаются либо математическими формулами, либо в виде таблиц и имеют определенные названия, как и элементы или схемы, их реализующие, причем часто одна и та же функция может иметь разные названия.

При математическом отображении этого процесса срабатывания логического элемента соответствует на выходе логической единице, отключение – логическому нулю, в зависимости от того, какие сигналы подаются на вход.

Общие условные обозначения простейших логических элементов имеют вид:

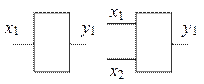
Математический аппарат анализа и синтеза цифровых систем – две переменные 0 и 1. Эти символы характеризуют состояние переменных или состояние их функций.

Различным соединением простейших ЛЭ друг с другом можно выполнять логическую функцию любой сложности. Для бесконтактных логических элементов обычно используют магнитные сердечники с прямоугольной петлей гистерезиса и полупроводниковые приборы. При этом ЛЭ могут быть выполнены:

- только на магнитных сердечниках, главным образом на сердечниках сложных форм – магнитные ЛЭ;

- на сочетании магнитных сердечников с полупроводниковыми приборами (диод, транзистор) – магнито-полупроводниковые ЛЭ;

- на полупроводниковых приборах, главным образом, на транзисторах – транзисторные ЛЭ.

В современных условиях широко применяются бесконтактные цифровые ЛЭ. По схеме исполнения операций цифровые логические элементы можно классифицировать:

- логический элемент – реализуют простейшие логические функции (первый низкий уровень функциональной интеграции);

- цифровой узел – совокупность логических элементов, имеет функциональную завершенность (средний уровень функциональной интеграции);

- цифровое устройство – комплекс узлов, выполняет на основе логических и цифровых операций сложные функции управления (высокий уровень функциональной интеграции);

- ЦВМ – комплекс цифровых устройств, (высший уровень).

Логические функции

Они могут быть записаны аналитически различными сочетаниями сложения и умножения переменных. Однако с точки зрения представления логических функций и последующего синтеза логической схемы наиболее удобны формы записи, при которых функция выражается либо в виде суммы произведений переменных, либо в виде их сумм

, .

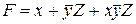Минимизация (упрощение формы записи) функции является важной операцией при синтезе логической схемы, так как это позволяет наименьшее число элементов.

Для этой цели наиболее удобным является метод карт Карно (при числе переменных до 5-6).

Карта образуется путем такого расположения клеток, при котором переменные соседних клеток отличаются только значением одной переменной. Соседними считают также крайние клетки каждого столбца или строки. Символ 1 характеризует прямое значение переменной, а символ 2 – ее инверсное значение.

В общем случае наличие единиц в 2^{2 n} соседних клеток позволяет исключить «n» переменных.

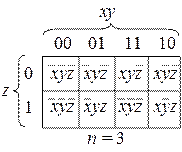
Число логических функций всегда конечно и равно N = 22 n, где n – число независимых переменных.

Одно из форм заданий логической функции – табличная, когда перечисляются все возможные комбинации значений аргументов и против каждой комбинации записывается значение функции.

Число возможных комбинаций при числе комбинаций – n равно 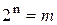, т.е при n = 4 – m = 16, n = 6 – m = 64; n = 10 – m = 1024.

Поиск по сайту: