Модель атома Томсона

Резерфорд предложил ядерную (планетарную) модель строения атома, в которой атом представлен в виде миниатюрной Солнечной системы. Согласно этой модели, весь положительный заряд и почти вся масса атома (99,4%) сосредоточены в атомном ядре. Размер ядра ничтожно мал по сравнению с размером атома. Вокруг ядра по замкнутым эллиптическим орбитам движутся электроны, образуя электронную оболочку атома. Заряд ядра равен суммарному заряду электронов.

2. Линейчатый спектр атома водорода.

Спектр излучения атомарного водорода состоит из отдельных спектральных линий, которые располагаются в определенном порядке. В 1885 г. Бальмер установил, что длины волн (или частоты) этих линий могут быть представлены формулой. Действительно, из (7) с учетом (6) для водорода (Z = 1), следует, что

, (8)

где R = 2,07× 10¹⁶ с ^-1 - постоянная Ридберга

Учитывая, что 1/l = v /с = w/2pс и используя (8), найдем

, (9)

где R =1,0974×10⁷ м^-1 - называется также постоянной Ридберга.

На рис. 1 изображена схема энергeтических уровней атома водорода, расчитанных согласно (6) при z=1.

При переходе электрона с более высоких энергетических уровней на уровень n = 1 возникает ультрофиолетовое излучение или излучение серии Лаймана (СЛ). Когда электроны переходя на уровень n = 2 возникает видимое излучение или излучение серии Бальмера (СБ). При переходе электронов с более высоких уровней на уровень n = 3 возникает инфракрасное излучение, или излучение серии Пашена (СП) и т.д.

Частоты или длины волн, возникающего при этом излучения, определяются по формулам (8) или (9) при m=1 - для серии Лаймана, при m=2 - для серии Бальмера и при m = 3 - для серии Пашена. Энергия фотонов определяется по формуле (7), которую с учетом (6) можно привести для водородоподобных атомов к виду:

эВ (10)

Теория Бора сыграла огромную роль в создании атомной физики.В период ее развития (1913 - 1925 г.) были сделаны важные открытия, например, в области атомной спектроскопии. Однако в теории Бора обнаружились существенные недостатки, например, с ее помощью невозможно создать теорию более сложных, чем атом водорода, атомов. Поэтому становилось очевидным, что теория Бора представляет собой переходной этап на пути создания последовательной теории атомных и ядерных явлений. Такой последовательной теорией явилась квантовая (волновая) механика.

3. Постулаты Бора.

Постулаты Бора — основные допущения, сформулированные Нильсом Бором в 1913 году для объяснения закономерности линейчатого спектра атома водорода и водородоподобных ионов (формула Бальмера-Ридберга) и квантового характера испускания и поглощения света. Бор исходил из планетарной модели атома Резерфорда.

Постулаты

Модель атома Бора

· Атом и атомные системы могут длительно пребывать только в особенных стационарных или квантовых состояниях, каждому из которых отвечает определенная энергия. В стационарном состоянии атом не излучает электромагнитных волн.

· Излучение света происходит при переходе электрона из стационарного состояния с большей энергией в стационарное состояние с меньшей энергией. Энергия излученного фотона равна разности энергий стационарных состояний.

Для получения энергетических уровней в атоме водорода в рамках модели Бора записывается второй закон Ньютона для движения электрона по круговой орбите в поле кулоновской силы тот притяжения

где m — масса электрона, e — его заряд, Z — количество протонов в ядре (атомный номер) и k — кулоновская константа, зависящая от выбора системы единиц. Это соотношение позволяет выразить скорость электрона через радиус его орбиты:

Энергия электрона равна разности кинетической энергии движения и его потенциальной энергии:

Используя правило квантования Бора, можно записать:

откуда радиус орбиты выражается через квантовое число n. Подстановка радиуса в выражение для энергии даёт:

≈ 13,6 эВ

4.Энергетический спектр водородоподобных атомов.

• Согласно третьему постулата Бора и соотношению для энергии атома водорода квант энергии, излучаемый (или поглощаемый) при переходе электрона в атоме из одного стационарного состояния в другое равен:

,
где – номера стационарных состояний, между которыми переходит электрон.

• Подобное соотношение можно записать для длины волны излучения (поглощения) кванта при переходе электрона внутри атома:

,
где – постоянная Ридберга для длины волны.

• Для частоты излучаемого кванта при переходе электрона внутри атома формула имеет вид:

,
где – постоянная Ридберга для частоты излучения.

• Для циклической частоты излучения получаем:

,
где – постоянная Ридберга для циклической частоты излучения.
Приведенные выше формулы верны и для поглощения, и для излучения кванта, в результате чего происходит переход электрона из одного стационарного состояния в другое. Если квантовое число , то (n) – номер ближней к ядру орбиты (более низкого энергетического уровня); (к) – номер дальней орбиты (более высокого энергетического уровня), тогда энергия поглощается. Наоборот, когда квант излучается, то электрон переходит с более далекой от ядра орбиты на более близкую, поэтому (n) – номер орбиты, на которую переходит электрон.
Из закономерностей для переходных процессов видно, что частоты (и соответственно длины волн) кванта не любые, а образуют дискретный ряд значений, что подтверждает экспериментальные данные о линейчатых спектрах излучения и поглощения атома водорода и водородоподобных атомов.

5. Корпускулярно - волновой дуализм свойств вещества.

Корпускуля́рно-волново́й дуали́зм (или Ква́нтово-волново́й дуали́зм) — принцип, согласно которому любой физический объект может быть описан как с использованием математического аппарата, основанного на волновых уравнениях, так и с помощью формализма, основанного на представлении об объекте как частице или системе частиц. В частности, волновое уравнение Шрёдингера не накладывает ограничений на массу описываемых им частиц, и следовательно, любой частице, как микро-, так и макро-, может быть поставлена в соответствие волна де Бройля. В этом смысле любой объект может проявлять как волновые, так икорпускулярные свойства^[1].

Идея о корпускулярно-волновом дуализме была использована при разработке квантовой механики для интерпретации явлений, наблюдаемых в микромире, с точки зрения классических концепций. В соответствии стеоремой Эренфеста квантовые аналоги системы канонических уравнений Гамильтона для макрочастиц приводят к обычным уравнениям классической механики. Дальнейшим развитием принципа корпускулярно-волнового дуализма стала концепция квантованных полей в квантовой теории поля.

Как классический пример, свет можно трактовать как поток корпускул (фотонов), которые во многих физических эффектах проявляют свойства электромагнитных волн. Свет демонстрирует свойства волны в явленияхдифракции и интерференции при масштабах, сравнимых с длиной световой волны. Например, даже одиночные фотоны, проходящие через двойную щель, создают на экране интерференционную картину, определяемую уравнениями Максвелла^[2]. Характер решаемой задачи диктует выбор используемого подхода: корпускулярного (фотоэффект, эффект Комптона), волнового или термодинамического^[3].

Тем не менее, эксперимент показывает, что фотон не есть короткий импульс электромагнитного излучения, например, он не может быть разделён на несколько пучков оптическими делителями лучей, что наглядно показал эксперимент, проведённый французскими физиками Гранжье, Роже и Аспэ в 1986 году^[4]. Корпускулярные свойства света проявляются при фотоэффекте и в эффекте Комптона. Фотон ведет себя и как частица, которая излучается или поглощается целиком объектами, размеры которых много меньше его длины волны (например, атомными ядрами), или вообще могут считаться точечными (например, электрон).

Сейчас концепция корпускулярно-волнового дуализма представляет лишь исторический интерес, так как, во-первых, некорректно сравнивать и/или противопоставлять материальный объект (электромагнитное излучение, например) и способ его описания (корпускулярный или волновой); и, во-вторых, число способов описания материального объекта может быть больше двух (корпускулярный, волновой, термодинамический, …), так что сам термин «дуализм» становится неверным. На момент своего возникновения концепция корпускулярно-волнового дуализма служила способом интерпретировать поведение квантовых объектов, подбирая аналогии из классической физики. На деле квантовые объекты не являются ни классическими волнами, ни классическими частицами, приобретая свойства первых или вторых лишь в некотором приближении. Методологически более корректной является формулировка квантовой теории через интегралы по траекториям (пропагаторная), свободная от использования классических понятий.

6. Некоторые свойства волн де Бройля.

• Пусть частица массы m движется со скоростью v. Тогда фазовая скорость волн де Бройля

.

Т.к. c > v, тофазовая скорость волнде Бройля больше скорости света в вакууме (v _ф может быть больше и может быть менше с, в отличие от групповой).

Групповая скорость

• следовательно, групповая скорость волн де Бройля равна скорости движения частицы.

Для фотона

т.е. групповая скорость равная скорости света.

• Волны де Бройля испытывают дисперсию. Подставив в получим, что v_ф = f (λ). Из-за наличия дисперсии волны де Бройля нельзя представить в виде волнового пакета, т.к. он мгновенно “ расплывется “ (исчезнет) за время 10^-26с.

7. Соотношения неопределенностей Гейзенберга.

Соотношение неопределенности Гейзенберга представляется как одно из основных, фундаментальных положений квантовой механики.
Приводим характеристику, данную этому соотношению Л. Д. Ландау:

“Открытие принципа неопределенности показало, что человек в процессе познания природы может оторваться от своего воображения, он может открыть и осознать даже то, что ему не под силу представить” [1].

Точка зрения Ландау отражает распространенное мнение о соотношении неопределенности Гейзенберга. Рассмотрим положения, в основном, сформулированные авторами квантовой механики, связанными с изложением и трактовкой этого соотношения, которые могут оправдать приведенную характеристику.

1. “Классическая физика как раз и кончается в том месте, где нельзя уже отказаться от учета влияния наблюдателя на исследуемые процессы” [2]. “Невозможность отдалить самостоятельное поведение от их взаимодействия с измерительными приборами, предназначенных для изучения условий протекания явления, влечет за собой неоднозначность в приписывании обычных атрибутов атомным явлениям. Это обстоятельство вызывает необходимость пересмотра нашего отношения к проблеме физического объяснения” [3].

Данный фактор, в действительности, имеет место и в процессе обычных измерений, описываемых с помощью классической механики. Но влияние измерительного прибора и методики измерения либо учитывается и вводится поправка, либо результат измерений фигурирует как условный, т. е. оговаривается методика. Во всяком случае, этот фактор достаточно очевидный и не выглядит парадоксальным.

2. “Специфическая неточность, обусловленная соотношением неопределенности, в классической физике отсутствует” [4].

“В квантовой механике мы встречаемся с парадоксальной ситуацией — наблюдаемые события повинуются закону случая… Сегодня порядок идей обратный [по сравнению с “предвзятыми идеями о причинности”]: случайность стала первичным понятием” [5,6]. “С точки зрения квантовой теории нет никакой причины, по которой [например] распались имменно эти ядра, они распались “просто так”, спонтанно. Квантовая теория предсказывает лишь вероятность распада ядер” [7].

В данном случае отрицается наличие причины происходящих явлений. Это часто используемый в квантовой механике способ “решения научных задач”: проблема “закрывается” путем провозглашения соответствующего “закона” или “принципа”. Для Борна “детерминизм” являлся ярлыком, характеризующим неприятие “современной” науки [6]. Его совершенно не устраивала и “компромиссная” теория “скрытых переменных”.

В основе мистического миропонимания лежит аналогичное восприятие необъяснимого: подразумевается, что феномен, недоступный нашему пониманию, находится вне сферы возможности его объяснения.

Следует отметить, что не все классики квантовой механики придерживались этой теории, в частности, против нее решительно выступал Планк: “eсли подобный шаг оказался бы действительно необходимым, то тем самым цель физического исследования была бы значительно отброшена назад, что нанесло бы значительный ущерб, значение которого нетрудно оценить” [8]. Тем не менее, подобное толкование “принципа неопределенности” вошло в ортодоксальную науку.

3. Соотношение неопределенности ряд авторов рассматривал как отражение волновых свойств частиц — следствие корпускулярно-волнового дуализма. “Соотношения неопределенности Гейзенберга непосредственно вытекают из положения, что элементами новой картины мира являются не материальные частицы, а простейшие периодические волны материи” [9]. “Соотношения неопределенности следуют из способа которым связываются с помощью постоянной h корпускулярная и волновая сторона единых объектов вещества и излучения” [9].

Однако эта точка зрения не является обоснованной, о чем, в частности, свидетельствует вывод соотношения Гейзенбергом без “непосредственного обращения к волновой картине с помощью математической схемы квантовой теории” [9].

4. Соотношение неопределенности Гейзенберга показывает, что “между точностью, с которой одновременно может быть установлено положение частицы, и точностью ее импульса существует определенное соотношение” [2]:

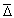q 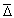p ≥ h, (1)
где 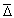— среднеквадратичное отклонение. Нетрадиционное обозначение в формуле вводится для того, чтобы подчеркнуть отличие 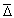от единичного отклонения, которое часто обозначается символом D, что в отдельных случаях вызывает неверное толкование формулы.

О неприятии данного соотношения в период становления квантовой теории свидетельствуют дискуссии между Эйнштейном и Бором и, в частности, т. н. “парадокс Эйнштейна – Подольского – Розена”, в котором предполагается “мысленное” одновременное измерение импульса и координаты у двух частиц – “двойников” [3, 7,9,10].

Характерная деталь: анализ приведенного выражения проводится так, как будто это эмпирическая формула, а не соотношение, полученное аналитическим путем. В результате трактовка соотношения оказывается не связанной с предпосылками и условностями, которые подразумевались при его выводе, и это является одной из причин тех парадоксов, которые связываются с данным соотношением. Конкретно, эти противоречия отметим в заключении нашего анализа.

Приводим относительно простой вывод соотношения, делая упор на исходные постулаты и условности.

1. В основе соотношения лежит формула Планка, отражающая положение о квантовании “действия ”:

E = n h
(E —энергия фотона, n — частота электромагнитной волны)

или ее следствия:

(p — импульс, l — длина волны).

Приращение “действия”, соответствующее h,

D S_h = p D q
(D q — приращение координаты)

или при одновременном изменении p и q [11]

D S_h = D p D q. (2)

2. Отметим, что проявление импульса невозможно без перемещения, а проявление энергии — вне времени. Под “проявлением” подразумевается регистрация путем взаимодействия объекта с наблюдателем, с измерительным прибором. Это условие справедливо и в классической механике.

3. В случае использования соотношения неопределенности, а возможно и в общем случае, измеряется “действие”, а не его компоненты — импульс, координаты, энергию, время.

Знаменательно — в действии объединены три основополагающие понятия: сила, длина, время. Измерительный же прибор “отградуирован”, соответственно, на импульс, координаты, энергию и время.

4. Неопределенность — это принципиальная невозможность определить величину параметра, а не результат влияния помех или ошибки измерения, подчиненных вероятностным законам, если их точное воздействие неизвестно.

Неопределенность, которую нельзя устранить, имеет место и в классической механике, она просто объясняется и легко воспринимается. Это случай, когда ограничена разрешающая способность конкретного измерительного инструмента: слишком велика при измерении “цена деления”, т. е. измерение осуществляется с помощью определенного шаблона, а требуется точность более высокая, чем та, что обеспечивается размерами или другими параметрами шаблона. Ни у кого, например, не вызывает удивления, что величина разрешения, достигаемого микроскопом, ограничена длиной волны в луче освещения. Эта неопределенность не связана с нашим незнанием причины погрешности, тем более, что этой причины не существует — у нас нет методики или инструмента для более точного определения измеряемого параметра.

5. В соотношении неопределенность рассматривается как фактор, вызывающий ошибку. Следовательно, формально предполагается стремление получить большую точность, чем та, которая может обеспечить дискретная величина кванта действия.

Если проводим измерение длины R линейкой с ценой деления r, то мы можем сказать, что гарантированная точность — ± r и абсолютная ошибка измерения — D R = r. Но если мы из результата измерения хотим оценить возможное значение R с большей точностью, чем допускается цена деления, то D R ≤ r.

Из примеров использования соотношения, которые приводит Гейзенберг [9], следует, что имеется в виду первый вариант, то есть под неопределенностью в соотношении понимается — невозможность определения значения параметра, связанная с его оценкой исключительно с той точностью, которая обеспечивается методикой.

Приведенные положения исходя из формулы (2) позволяют выразить, в соответствии с п. 5, ошибку измерения действия

D S ≥ D p D q ≥ D S_h = h (3)
D S ≥ D E D t ≥ D S_h = h (4)

Если соотношению удовлетворяют каждое конкретное измерение, то ему соответствует результат при их статистической обработке — (1), и его разновидность — соотношение неопределенности Бора:

E t ≥ h. (5)

Выражения (1) и (5), включающими усредненную погрешность, не являются основными — они приводятся в связи с традиционным представлениям соотношения. Значительно большее теоретическое и практическое содержание заключено в формулах (3), (4).

Традиционное выражение соотношения связано с укоренившимся взглядом на волновые свойства частиц, который представляется цепочкой: частица — волновой пакет — вероятностная интерпретация волновой функции, по которой рассматривается только вероятность характеристик частицы. Даже тогда, когда Гейзенберг выводит соотношение “без обращения к волновой картине”, он рассматривает среднеквадратичное отклонение p и q, при этом приписывает этим величинам гауссовское распределение вероятности [5], хотя, как указывалось, основной фактор, влияющий на погрешность, не связан со случайными воздействиями, да их и может не существовать. Использование волновой функции [12,13], даже, считая ее абстракцией, затмевает физическую сущность соотношения.

Выводы

Изложенное меняет распространенное представление о соотношении неопределенности и связанных с ней парадоксах.

1. Влияние измерительного инструмента н одновременное его воздействие на результат измерения сопряженных параметров не является спецификой квантовой механики и рассматриваемого соотношения. Специфичным является феномен квантования “действия”.
2. Соотношение неопределенности не отражает волновых свойств частиц [14] (см. в настоящем сборнике: Бернштейн В. М. Развитие электродинамики Гаусса – Вебера. Квантовая механика без волновой теории.)
3. Специфическая неопределенность соответствует невозможности определения параметров отдельной частицы и не отражает вероятностный подход, относящийся к ансамблю частиц.
4. Специфическая неопределенность отдельно каждого из сопряженных параметров определяется методикой измерения.

Связь между точностями измерения сопряженных параметров имеет место не просто при одновременном измерении обоих параметров, а при едином измерении, соответствующим определению количества квантов действия с параллельной, зависящей от используемой методики измерения, оценкой их компонентов — сопряженных параметров. Моделью подобного измерения является индикатор, в котором имеются три шкалы, отградуированные не только в квантах действия, но и в измеряемых сопряженных параметрах.

Следовательно, “парадокс Эйнштейна – Подольского – Розена” с отдельным измерением параметров “частиц-близнецов” не соответствует условиям, на которые распространяется соотношение неопределенности. Соответственно, и соотношение не выглядит столь парадоксальным.

Поиск по сайту: