Статистические методы анализа систем управления

Регрессионный анализ

Регрессионный анализ ставит своей задачей исследование зависимости одной случайной величины от ряда других случайных и неслучайных величин (регрессия — зависимость математического ожидания случайной величины от значений других случайных величин). Например, после проведения N экспериментов на статистической модели получен набор реализаций случайных величин является независимой переменной, а X — функцией. Обработка этого массива случайных величин позволяет представить их в виде детерминированной линейной регрессивной модели типа: где коэффициенты а и b рассчитываются согласно методу наименьших квадратов таким образом, чтобы квадраты отклонений случайных величин Y от значений функций на множестве X, были наименьшими, т.е. В случае нескольких независимых переменных регрессивная модель представляется линейным полиномом:

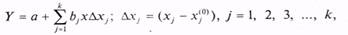
Данное выражение представляет собой функцию, однако, если значения достаточно велики или функция Y. существенно нелинейна, то можно использовать разложение более высокого порядка.

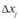Точность и надежность получаемых оценок зависят от числа наблюдений (реализаций, экспериментов) и расположения прогностических значений относительно базовых (т.е. известных на некоторый момент времени) Чем больше разность тем меньше точность прогноза.

Корреляционный анализ

Корреляционный анализ используется для определения степени линейной взаимосвязи между случайными величинами (корреляция — зависимость между случайными величинами, выражающая тенденцию одной величины возрастать или убывать при возрастании или убывании другой).

Основными задачами корреляционного анализа являются оценка корреляционных характеристик и проверка статистических гипотез о степени (значимости) связи между случайными величинами.

Корреляционной характеристикой является коэффициент корреляции, равный математическому ожиданию произведений отклонений случайных величин и от своих математических ожиданий и нормированный относительно среднеквадратических отклонений данных случайных величин.

Оценки коэффициентов корреляции рассчитываются по значениям оценок математических ожиданий и среднеквадратических отклонений, полученных путем статистической обработки результатов реализаций случайных величин.

Дисперсионный анализ

Дисперсионный анализ используется для проверки статистических гипотез о влиянии качественных факторов на показатели, т.е. факторов, не поддающихся количественному измерению (например, качественный фактор — организация производства, влияющий на количественный показатель — прибыль от производства). В этом заключается его отличие от регрессионного анализа, в котором факторы имеют количественную меру (например, количественный фактор — затраты на производство).

Ковариационный анализ

Ковариационный анализ используется для создания и изучения вероятностных моделей процессов, в которых присутствуют одновременно как количественные, так и качественные факторы, т.е. он объединяет регрессионные и дисперсионные методы. Модель включает в себя регрессионные и дисперсионные факторы, первые служат для проверки гипотез о значимости количественных факторов, а вторые качественных.

Метод временных рядов

Анализ временных рядов используется при исследовании дискретного случайного процесса, протекающего на интервале времени Т.

Результаты экспериментов или наблюдений, полученные на данном интервале, представляются в виде временного ряда, каждое значение Y которого включает детерминированную f(t) и случайную z(t) составляющие:

Y= f(t)+ z(t).

Детерминированная составляющая описывает влияние детерминированных факторов в момент времени t, влияние же множества случайных факторов описывает случайная составляющая. Детерминированную часть временного ряда называют трендом. Этот временной ряд описывается так называемой трендовой моделью:

где а0, а. — коэффициенты тренда;

k — количество функций времени, линейная комбинация которых определяет детерминированную составляющую;

— функция времени.

С помощью этого случайного процесса в виде временных рядов можно, во-первых, исследовать динамику этого процесса, во-вторых, выделить факторы, существенным образом влияющие на показатели, и определить периодичность их максимального воздействия, в-третьих, провести интегральный или точечный прогноз показателя Y на некоторый промежуток времени.

Метод главных компонентов

Метод главных компонентов используется при рассмотрении некоторого множества случайных значений показателей Y в целях определения общих для них факторов (компонентов), от которых все они зависят. Степень зависимости i-го показателя от j-го компонента отражается величиной а, называемой нагрузкой i -го показателя на j-й компонент. Результатом анализа является модель главных компонентов, в которой каждый показатель представлен суммой произведений компонентов и их нагрузок:

где f — центрированные, нормированные и некоррелированные компоненты. Модель главных компонентов показывает, что и в какой степени определяет исследуемые показатели, а также объясняет связи между ними.

Факторный анализ

Факторный анализ по своей сути совпадает с методом главных компонентов, однако позволяет представить показатели через меньшее количество факторов (компонентов), поэтому используется при исследовании сложных систем управления, с большим числом показателей и сложными взаимосвязями между ними. Предполагается, что за множеством показателей системы стоит небольшое число независимых скрытых параметров, называемых факторами.

Поиск по сайту: