Механика твёрдого тела

● Момент инерции материальной точки

,

где m- масса материальной точки; r- расстояние до оси вращения.

●Момент инерции системы материальных точек (тела)

,

где r_i – расстояние от материальной точки массы m_i до оси вращения. В случае непрерывного распределения массы .

●Теорема Штейнера

,

где J₀ – момент инерции относительно оси, проходящей через центр масс; J – момент инерции относительно произвольной оси, параллельной данной, отстоящей от первой на расстоянии ; m- масса тела.

● Кинетическая энергия тела, вращающегося вокруг неподвижной оси z

,

где J_z- момент инерции тела относительно оси z; ω- его угловая скорость.

●Кинетическая энергия тела, движущегося поступательно без скольжения при одновременном вращении

,

где J₀ – момент инерции относительно оси, проходящей через центр масс; m- масса тела; – скорость центра масс тела; ω- угловая скорость тела.

● Момент силы относительно неподвижной точки

,

где r – радиус-вектор, проведенный из этой точки в точку приложения силы F. Модуль момента силы

,

где - плечо силы (кратчайшее расстояние между линией действия силы и осью вращения).

● Работа при вращении тела

,

где - угол поворота тела; - момент силы относительно оси z.

● Момент импульса

.

● Момент импульса твердого тела относительно произвольной оси z

,

где r_i – расстояние от оси до отдельной частицы тела; 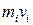- импульс этой частицы; J_z – момент инерции тела относительно оси z; ω – его угловая скорость.

● Уравнение (закон) динамики вращательного движения твердого тела

.

● Уравнение (закон) динамики вращательного движения твердого тела относительно неподвижной оси z

,

где ε – угловое ускорение; J_z – момент инерции тела относительно оси z.

● Механическое напряжение при упругой деформации

,

где F- растягивающая (сжимающая) сила; S – площадь поперечного сечения.

● Закон Гука для продольного растяжения (сжатия)- ,

где E – модуль Юнга, ε – относительное приращение длины стержня .

Поиск по сайту: