 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Принцип аргумента
Запишем характеристический полином САУ в виде
D(p) = a0  (p - p1)
(p - p1)  (p - p2)
(p - p2)  ...
...  (p - pn) = 0.
(p - pn) = 0.

Его корни
pi = 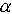 i + j
i + j  i = |pi|ejarg(pi),
i = |pi|ejarg(pi),
где arg(pi) = arctg( i/ai) + k
i/ai) + k  ,
,
 .
.
Каждый корень можно изобразить вектором на комплексной плоскости (рис.68а), тогда разность p - pi изобразится разностью векторов (рис.68б), где p - любое число.
Еcли менять значение p произвольным образом, то конец вектора p - pi будет перемещаться по комплексно плоскости, а его начало будет оставаться неподвижным, так как pi - это конкретное неизменное значение.
В частном случае, если на вход системы подавать гармонические колебания с различной частотой  , то p = j
, то p = j  , а характеристический полином принимает вид:
, а характеристический полином принимает вид:
D(j  ) = a0
) = a0  (j
(j  - p1)
- p1)  (j
(j  - p2)
- p2)  ...
...  (j
(j  - pn).
- pn).
При этом концы векторов j  - pi будут находиться на мнимой оси (рис.68в). Если менять
- pi будут находиться на мнимой оси (рис.68в). Если менять  от -
от - 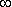 до +
до + 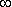 , то каждый вектор j
, то каждый вектор j  - pi будет поворачиваться относительно своего начала pi на угол +p для левых и - p для правых корней (рис.68г).
- pi будет поворачиваться относительно своего начала pi на угол +p для левых и - p для правых корней (рис.68г).
Характеристический полином можно представить в виде
D(j  ) = |D(j
) = |D(j  )|ejarg(D(j
)|ejarg(D(j  )),
)),
где |D(j  )| = a0
)| = a0  |j
|j  - p1|
- p1|  |j
|j  - p2|...|j
- p2|...|j  - pn|,
- pn|,
arg(D(j  )) = arg(j
)) = arg(j  - p1) + arg(j
- p1) + arg(j  - p2) +.. + arg(j
- p2) +.. + arg(j  - pn).
- pn).
Пусть из n корней m - правые, а n - m - левые, тогда угол поворота вектора D(j  ) при изменении
) при изменении  от -
от - 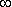 до +
до + 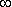 равен
равен
 = (n - m)
= (n - m)  - m
- m  ,
,
или при изменении  от 0 до +
от 0 до + 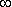 получаем
получаем
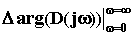 = (n - 2m)
= (n - 2m)  (
( /2).
/2).
Отсюда вытекает правило: изменение аргумента вектора b при изменении частоты  от -
от - 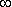 до +
до + 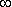 равно разности между числом левых и правых корней уравнения D(p) = 0, умноженному на
равно разности между числом левых и правых корней уравнения D(p) = 0, умноженному на  , а при изменении частоты
, а при изменении частоты  от 0 до +
от 0 до + 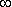 эта разность умножается на
эта разность умножается на  /2.
/2.
Это и есть принцип аргумента. Он положен в основе всех частотных критериев устойчивости. Мы рассмотрим два наиболее распространенных критерия: критерий Михайлова и критерий Найквиста.
Поиск по сайту: