 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Розв’язок
|
Читайте также: |
1) Важливим напрямком у статистичному зведенні є побудова рядів розподілу, одне з призначень яких складається у вивченні структури досліджуваної сукупності, характеру і закономірності розподілу.
Ряд розподілу– це найпростіше групування, що представляє собою розподіл чисельності одиниць сукупності за значенням якої-небудь ознаки.
Ряди розподілу, в основі яких лежить якісна ознака, називають атрибутивним. Якщо ряд побудований по кількісній ознаці, його називають варіаційним, який і буде побудовано в нашій задачі, тобто коефіцієнт конкурентоспроможності є кількісною ознакою.
При побудові варіаційного ряду з рівними інтервалами визначають число його груп ( ) і величину інтервалу (
) і величину інтервалу ( ).
).
Величина рівного інтервалу розраховується по формулі:
 (1)
(1)
де  – число виділених інтервалів.
– число виділених інтервалів.
Оптимальне число груп може бути визначено по формулі Стерджеса:
 , (2)
, (2)
Де n - число одиниць сукупності.
Визначимо величину інтервалу по формулі (1), підставивши у знаменник формулу (2):

Отримаємо наступні інтервали:
0,615 – 0,638;
0,638 – 0,661;
0,661 – 0,684;
0,684 – 0,707;
0,707 – 0,730;
0,730 – 0,754.
Розподіл туристичних фірм за коефіцієнтом конкурентоспроможності
| № групи | Коефіцієнт конкурентоспроможності | Значення коефіцієнта конкурентоспроможності | Кількість тур. фірм |
| I | 0,615 – 0,638 | 0,615 | |
| 0,632 | |||
| 0,634 | |||
| II | 0,638 – 0,661 | 0,645 | |
| 0,649 | |||
| 0,652 | |||
| 0,656 | |||
| 0,661 | |||
| III | 0,661 – 0,684 | 0,663 | |
| 0,666 | |||
| 0,668 | |||
| 0,670 | |||
| 0,673 | |||
| 0,678 | |||
| 0,678 | |||
| IV | 0,684 – 0,707 | 0,687 | |
| 0,694 | |||
| 0,701 | |||
| 0,703 | |||
| V | 0,707 – 0,730 | 0,720 | |
| 0,723 | |||
| VI | 0,730 – 0,754 | 0,754 | |
| 0,754 | |||
| S |
Зобразимо графічно побудований ряд розподілу:

Рис. 1 Розподіл туристичних фірм за коефіцієнтом конкурентоспроможності
2) Середня є узагальнюючою характеристикою сукупності одиниць по якісно однорідній ознаці.
У статистиці застосовуються різні види середніх: арифметична, гармонійна, квадратична, геометрична і структурні середні – мода і медіана. Середні, крім моди і медіани, обчислюються в двох формах: простій і зваженій. Вибір форми середньої залежить від вихідних даних і змісту обумовленого показника. Найбільше поширення одержала середня арифметична, як проста, так і зважена.
В нашій задачі дані представлені у вигляді інтервального ряду розподілу, в якому однакові значення ознаки ( ) об'єднані в групи, що мають різне число одиниць (
) об'єднані в групи, що мають різне число одиниць ( ), яке називається частотою (вагою), тому застосовується середня арифметична зважена:
), яке називається частотою (вагою), тому застосовується середня арифметична зважена:

(3)
де  – значення ознаки (варіант);
– значення ознаки (варіант);
 – число одиниць ознаки;
– число одиниць ознаки;

 – загальне значення ознаки.
– загальне значення ознаки.
Розрахуємо серединні значення для кожного інтервалу та зважування:
| № групи | Коефіцієнт конкурентоспроможності | Кількість одиниць сукупності, 
| Кумулятивні частоти | Серединне значення інтервалу, 
| 
|
| I | 0,615 – 0,638 | 
| 1,8795 | ||
| II | 0,638 – 0,661 | 
| 3,2475 | ||
| III | 0,661 – 0,684 | 
| 4,7075 | ||
| IV | 0,684 – 0,707 | 
| 2,782 | ||
| V | 0,707 – 0,730 | 
| 1,437 | ||
| VI | 0,730 – 0,754 | 
| 1,484 | ||
| S | 15,5375 |
Середнє значення коефіцієнта конкурентоспроможності становитиме:

3)Середня арифметична є узагальнюючою характеристикою сукупності за тією або іншою варіаційною ознакою. Водночас структуру цієї сукупності характеризують особливими показниками, які називають у статистиці структурними середніми величинами. Зокрема, це мода і медіана.
Мода  –це величина ознаки, яка найчастіше трапляється в ряді розподілу і обчислюється за формулою:
–це величина ознаки, яка найчастіше трапляється в ряді розподілу і обчислюється за формулою:
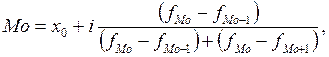 (4)
(4)
де  – нижня межа модального інтервалу (такого, в якому найбільша кількість одиниць сукупності);
– нижня межа модального інтервалу (такого, в якому найбільша кількість одиниць сукупності);
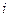 – величина модального інтервалу;
– величина модального інтервалу;
 – частота модального інтервалу;
– частота модального інтервалу;
 – частота попереднього і наступного інтервалів відносно модального.
– частота попереднього і наступного інтервалів відносно модального.
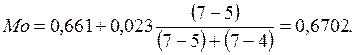
Медіана  вказує на значення варіаційної ознаки, якого досягла половина одиниць сукупності.
вказує на значення варіаційної ознаки, якого досягла половина одиниць сукупності.
Для обчислення медіани спочатку в інтервальному ряді розподілу визначають медіанний інтервал. Він відповідає такому, кумулятивна частота якого дорівнює або перевищує половину суми частот. Кумулятивні частоти дістають поступовим підсумовуванням частот, розпочинаючи з інтервалу з найменшим значенням ознаки.
Медіана обчислюється за формулою:
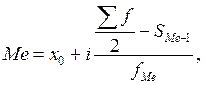 (5)
(5)
де  – нижня межа медіанного інтервалу;
– нижня межа медіанного інтервалу;
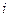 – величина медіанного інтервалу;
– величина медіанного інтервалу;
 – частота медіанного інтервалу;
– частота медіанного інтервалу;
 – частота медіанного інтервалу.
– частота медіанного інтервалу.

Порівнюючи середню арифметичну, моду і медіану, ми побачимо, що співвідношення цих величин наближено до нормального закону розподілу.
4) Для виміру ступеня коливання окремих значень ознаки від середньої обчислюються основні узагальнюючі показники варіації: дисперсія, середнє квадратичне відхилення і коефіцієнт варіації.
Дисперсія( ) – це середня арифметична квадратів відхилень окремих значень ознаки від їхньої середньої арифметичної. Для згрупованих даних дисперсія обчислюється по формулі середньої арифметичної зваженої:
) – це середня арифметична квадратів відхилень окремих значень ознаки від їхньої середньої арифметичної. Для згрупованих даних дисперсія обчислюється по формулі середньої арифметичної зваженої:
 , (6)
, (6)
Середнє квадратичне відхилення показує, наскільки в середньому відрізняються індивідуальні значення ознаки від середньої. Середнє квадратичне відхилення являє собою корінь квадратний з дисперсії і для згрупованих даних дорівнює:
 , (7)
, (7)
Відносний показник варіації – коефіцієнт варіації ( ) – є певною мірою критерієм типовості середньої. Він вживається для оцінки однорідності сукупності. Сукупність є однорідною, а середня – типовою, якщо коефіцієнт варіації не перевищує 33 %. Коефіцієнт варіації являє собою процентне відношення середнього квадратичного відхилення і середньої арифметичної:
) – є певною мірою критерієм типовості середньої. Він вживається для оцінки однорідності сукупності. Сукупність є однорідною, а середня – типовою, якщо коефіцієнт варіації не перевищує 33 %. Коефіцієнт варіації являє собою процентне відношення середнього квадратичного відхилення і середньої арифметичної:
 , (8)
, (8)
Для зручності розрахунків потрібні дані представимо в таблиці:
| Коефіцієнт конкурентоспроможності | Кількість
фірм,

| Середина
інтервалу,

| 
| 
| 
|
| 0,615 – 0,638 | 0,6265 | 0,049 | 0,002401 | 0,007203 | |
| 0,638 – 0,661 | 0,6495 | 0,026 | 0,000676 | 0,00338 | |
| 0,661 – 0,684 | 0,6725 | 0,003 | 0,000009 | 0,000063 | |
| 0,684 – 0,707 | 0,6955 | 0,02 | 0,0004 | 0,0016 | |
| 0,707 – 0,730 | 0,7185 | 0,043 | 0,001849 | 0,003698 | |
| 0,730 – 0,754 | 0,742 | 0,0665 | 0,004422 | 0,008844 | |
| S | 0,024788 |
Дисперсія:


Середнє квадратичне відхилення:


Коефіцієнт варіації:
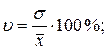

Так як коефіцієнт варіації становить всього 4,86%, сукупність є однорідною, а середня – типовою.
5)Оцінимо взаємозв’язок коефіцієнта конкурентоспроможності з пасажирообігом, використовуючи метод аналітичних групувань.
Аналітичне групування дозволяє вивчати взаємозв'язок факторної і результативної ознак.
Основні етапи проведення аналітичного угруповання – обґрунтування і вибір факторної 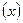 і результативної
і результативної  ознак; визначення оптимального числа груп і меж інтервалів (з розрахунком, що групові середні будуть мати не випадковий характер і щоб групувальна ознака проявила себе повною мірою); підрахунок числа одиниць у кожній з утворених груп; визначення обсягу ознак, що варіюють у межах створених груп, а також підрахування середніх значень як факторної, так і результативної ознак. Порівнюючи зміни середніх значень обох ознак, виявляють характер зв’язку між ними.
ознак; визначення оптимального числа груп і меж інтервалів (з розрахунком, що групові середні будуть мати не випадковий характер і щоб групувальна ознака проявила себе повною мірою); підрахунок числа одиниць у кожній з утворених груп; визначення обсягу ознак, що варіюють у межах створених груп, а також підрахування середніх значень як факторної, так і результативної ознак. Порівнюючи зміни середніх значень обох ознак, виявляють характер зв’язку між ними.
Для побудови аналітичного групування необхідно визначити яка ознака являється факторною, а яка результативною. В даному прикладі коефіцієнт конкурентоспроможності – факторна ознака, а пасажирообіг залежить від конкурентоспроможності, тому це результативна ознака.
По факторній ознаці (коефіцієнт конкурентоспроможності) будуємо ряд розподілу, що було зроблено раніше, тому використаємо цю побудову.
Групування туристичних фірм по пасажирообігу від коефіцієнта конкурентоспроможності.
| № групи | Групування по коефіцієнту конкурентоспроможності | Кількість одиниць сукупності | Значення коефіцієнтів конкурентоспроможності (Х) | Значення паса жирообігу, 
| Загальне значення паса жирообігу,( ) )
| Середнє значення паса жирообігу, ( ) )
|
| I | 0,615-0,638 | 0,615 | 264,5 | 877,4 | 292,5 | |
| 0,632 | 355,4 | |||||
| 0,634 | 257,5 | |||||
| ІІ | 0,638-0,661 | 0,645 | 671,3 | 2159,5 | 431,9 | |
| 0,649 | 538,2 | |||||
| 0,652 | 235,3 | |||||
| 0,656 | 343,7 | |||||
| 0,661 | 371,0 | |||||
| ІІІ | 0,661-0,684 | 0,663 | 245,6 | 2184,5 | 312,0 | |
| 0,666 | 291,7 | |||||
| 0,668 | 214,3 | |||||
| 0,670 | 312,0 | |||||
| 0,673 | 393,7 | |||||
| 0,678 | 269,3 | |||||
| 0,678 | 457,9 | |||||
| ІУ | 0,684-0,707 | 0,687 | 251,3 | 2264,5 | 566,1 | |
| 0,694 | 447,4 | |||||
| 0,701 | 873,4 | |||||
| 0,703 | 692,4 | |||||
| У | 0,707-0,730 | 0,720 | 192,2 | 1204,7 | 602,3 | |
| 0,723 | 1012,5 | |||||
| УІ | 0,730-0,734 | 0,754 | 1995,4 | 2996,4 | 1498,2 | |
| 0,754 | 1001,0 |
За даними аналітичного групування ми бачимо, що із збільшенням коефіцієнту конкурентоспроможності пасажирообіг зростає.
Виходить, між досліджуваними ознаками існує пряма кореляційна залежність.
Для кількісної оцінки зв’язку між явищами на базі матеріалів аналітичного групування розраховуємо кореляційне відношення ( ).
).
Кореляційне відношеннявказує на ступінь варіації ознаки під впливом фактора, покладеного в основу групування ідорівнює відношенню міжгрупової дисперсії до загальної:

де  – міжгрупова дисперсія, що знаходиться по формулі:
– міжгрупова дисперсія, що знаходиться по формулі:
 , (8)
, (8)
 – загальна дисперсія результативної ознаки, що знаходиться по формулі:
– загальна дисперсія результативної ознаки, що знаходиться по формулі:
 , (9)
, (9)
Якісно оцінити щільність зв’язку між досліджуваними ознаками на підставі емпіричного кореляційного відношення можна за допомогою такої шкали:
Показник 
| 0,1...0,3 | 0,3...0,5 | 0,5...0,7 | 0,7...0,9 | 0,9...0,99 |
| Зв’язок | Слабкий | Помірний | Помітний | Сильний | Дуже сильний |
По абсолютній величині він може змінюватися від 0 до 1. Якщо 
 , то всі групові середні однакові і кореляційний зв’язок між ознаками відсутній. Якщо
, то всі групові середні однакові і кореляційний зв’язок між ознаками відсутній. Якщо 
 , то міжгрупова дисперсія дорівнює загальній, а середня з групових – нулю, тобто зв'язок між ознаками функціональний.
, то міжгрупова дисперсія дорівнює загальній, а середня з групових – нулю, тобто зв'язок між ознаками функціональний.
| № групи | Групування по коефіцієнту конкурентоспроможності (Х) | Кількість одиниць сукупності, (f) | Середнє значення пасажирообігу,

| 
| 
| 
|
| 0,615-0,638 | 292,5 | -215,6 | 46483,4 | 139450,0 | ||
| 0,638-0,661 | 431,9 | -76,2 | 5806,4 | 29032,2 | ||
| 0,661-0,684 | 312,0 | -196,1 | 38455,2 | 269186,5 | ||
| 0,684-0,707 | 566,1 | |||||
| 0,707-0,730 | 602,3 | 94,2 | 8873,6 | 17747,2 | ||
| 0,730-0,754 | 1498,2 | 990,1 | ||||
| Разом | 508,1 | - | - |
Знаходимо міжгрупову дисперсію:



Знаходимо загальну дисперсію:

Обчислюємо коефіцієнт детермінації:

Кореляційне відношення показує, що пасажирообіг на 66,4% залежить від коефіцієнта конкурентоспроможності на 33,6% від неврахованих факторів.
Це говорить про те, що зв'язок між факторною і результативною ознаками помітний (згідно шкали), тобто свідчить про достатній вплив коефіцієнта конкурентоспроможності на пасажирообіг.
Зобразимо графічно результати аналітичного групування:

Поиск по сайту: