 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Контрольная работа № 1
В задачах 1-20 решить и исследовать заданную систему уравнений, пользуясь формулами Крамера. Сделать проверку полученного решения.
| 1. | 3x + 6y – z = - 7, x + 2y + 3z = 1, 2x – 3y + 2z = 9. | 8. | 3x – y = 5, -2x + y + z = 0, 2x – y + 4z = 15. | 15. | x + 9y + 2z = 18, 2x – y – 3z = -1, x + 5y + z = 0. |
| 2. | 7x + 2y + z = 4, 3x – 5y + 3z = 1, 2x + y – z = 8. | 9. | 3x – y + z = 4, 2x – y – 7z = -17, 8x + 5y – z = 0. | 16. | 4x – y + z = 17, x + 3y – 2z = 0, 2y – z = 2. |
| 3. | 3x + 2y + z = 5, 2x + 9y + z = 1, 5x + y + 3z = 11. | 10. | x + y + z = 2, 2x – y – 6z = -1, 3x – 2y = 8. | 17. | 2x + y + 4z = 20, 2x – y – 3z = 3, 3x + 4y – 5z = -8. |
| 4. | x + 2y + 4z = 30, 5x + y + 2z = 29, 3x – y + z = 19. | 11. | 2x + y – z = 1, x + y + z = 6, 3x – y + z = 4. | 18. | x – y = 4, 2x + 3y + z = 1, 2x + y + 3z = 11. |
| 5. | x – 3y + 2z = 9, 2x + 5y – 3z = 4, x + 6y – 2z = 14. | 12. | 2x – y – 3z = 3, 3x + 4y – 5z = 8, 2y + 7z = 17. | 19. | x + 5y – z = 7, 2x – y –2z = 14, 3x – 2y + 4z = 11. |
| 6. | 2x – y – z = 4, 3x + 4y – 2z = 11, x – 2y + 4z = 12. | 13. | x + 5y + z = -7, 2x – y – z = 0, x – 2y – z = 2. | 20. | 14x + 5y – z = 2, 2x + 5y – 5z = 15, x + y + z = 2. |
| 7. | x + y + 2z = -1, 2x – y + 2z = -4, 7x + y + 4z = -3. | 14. | x – 4y + 5z = 16, x + 3y – 4z = 8, 3x – 2y – 5z = 12. |
Решение типового примера.
Решить систему уравнений с помощью определителей (по формулам Крамера).
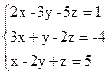
Формула Крамера имеет вид:  , где Δ
, где Δ  0 – определитель системы, состоящий из коэффициентов при неизвестных а Δх, Δу, Δz – побочные определители, составленные из определителя системы, заменой столбца коэффициентов при соответствующем неизвестном столбцом свободных членов.
0 – определитель системы, состоящий из коэффициентов при неизвестных а Δх, Δу, Δz – побочные определители, составленные из определителя системы, заменой столбца коэффициентов при соответствующем неизвестном столбцом свободных членов.
Имеем, 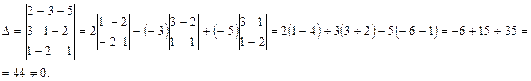
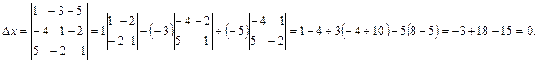
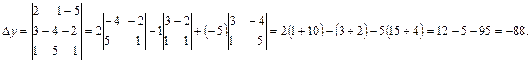
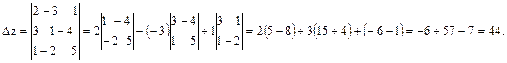
По формулам Крамера имеем  . Подставляя найденные значения х=0, у=-2, z=1 в каждое уравнение системы убеждаемся в справедливости равенств.
. Подставляя найденные значения х=0, у=-2, z=1 в каждое уравнение системы убеждаемся в справедливости равенств.
Замечание. Вычисление определителей мы проводим разложением их по элементам первой строки:
 , где определитель второго порядка вычисляется по формуле:
, где определитель второго порядка вычисляется по формуле:
 .
.
В задачах 21-40 даны координаты вершин треугольника АВС. Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) внутренний угол В в радианах с точностью до 0,01; 4) уравнение медианы АЕ; 5) уравнение и длину высоты СD; 6) уравнение прямой, проходящей через точку Е параллельно стороне АВ и точку М ее пересечения с высотой СD.
| 21. | А (2; -2), В (-1; 3), С (5; 1). | 31. | А (2; 2), В (5; 6), С (6; 4). |
| 22. | А (0; -1), В (3; 5), С (2; 1). | 32. | А (4; -2), В (3; 2), С (0; 0). |
| 23. | А (3; -2), В (4; 2), С (5; 0). | 33. | А (0; 2), В (3; 6), С (4; 4). |
| 24. | А (2; -2), В (5; 2), С (6; 0). | 34. | А (4; 1), В (9; 5), С (8; 3). |
| 25. | А (0; 0), В (5; 4), С (4; 2). | 35. | А (6; 2), В (3; 6), С (7; 4). |
| 26. | А (0; 1), В (3; 5), С (4; 3). | 36. | А (-2; 1), В (1; 5), С (2; 3). |
| 27. | А (3; -2), В (0; 2), С (7; 0). | 37. | А (4; -3), В (7; 1), С (8; -1). |
| 28. | А (3; -3), В (6; 1), С (7; -1). | 38. | А (-2; 2), В (1; 0), С (2; 4). |
| 29. | А (-1; 1), В (2; -4), С (3; 1). | 39. | А (5; 0), В (4; 4), С (9; 2). |
| 30. | А (4; 1), В (0; 4), С (8; 2). | 40. | А (9; 3), В (5; 7), С (6; 7). |
Решение типового примера.
Пусть А (-8;-3), В (4;-12), С (8;10).
1) Длину АВ найдем по формуле:  , имеем
, имеем
 .
.
2) Уравнение сторон АВ и ВС найдем по формуле
 .
.
Для стороны АВ имеем уравнение
 или
или  или
или 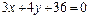 .
.
Для нахождения углового коэффициента прямой представим ее уравнение в виде  где k – угловой коэффициент (тангенс угла между прямой и осью Ох). Получим
где k – угловой коэффициент (тангенс угла между прямой и осью Ох). Получим  . Т.о.
. Т.о.  .
.
Для стороны ВС имеем уравнение 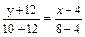 или
или  или
или  или
или  . Т.о.
. Т.о. 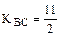 .
.
3) Внутренний угол при вершине В (из чертежа видно, что он острый) найдем по формуле:  . Имеем,
. Имеем,  . Таким образом,
. Таким образом,  .
.
4) Для нахождения уравнения медианы АЕ найдем координаты точки Е (середина отрезка ВС)  .
.
Итак, Е (6;-1) и уравнением АЕ будет  или
или  или
или  . Окончательно, уравнение АЕ имеет вид
. Окончательно, уравнение АЕ имеет вид  .
.
5) Для нахождения уравнения высоты СD найдем ее угловой коэффициент из условия перпендикулярности прямых АВ и СD. Имеем  . Теперь используя формулу уравнения прямой, проходящей через заданную точку
. Теперь используя формулу уравнения прямой, проходящей через заданную точку  , составим уравнение высоты СD.
, составим уравнение высоты СD.  или
или  , или
, или  .
.
Длину высоты СD найдем по формуле  - расстояние от точки С до прямой АВ. Имеем
- расстояние от точки С до прямой АВ. Имеем 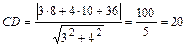 .
.
6) Прямая ЕМ, параллельная АВ имеет угловой коэффициент  . Поэтому ее уравнение имеет вид:
. Поэтому ее уравнение имеет вид:  или
или  . Найдем точку ее пересечения с высотой СD из системы уравнений
. Найдем точку ее пересечения с высотой СD из системы уравнений  . Решая систему уравнений, получим х=2, у=2. Таким образом, М (2;2).
. Решая систему уравнений, получим х=2, у=2. Таким образом, М (2;2).
В ЗАДАЧАХ 61-80 найдем указанные пределы
61. а) 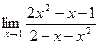 ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  .
62. а) .
62. а)  ;
б) ;
б) 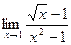 ;
в) ;
в)  ;
г) ;
г)  .
63. а) .
63. а)  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  . .
| 64. а)  ;
б) ;
б) 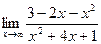 ;
в) ;
в)  ;
г) ;
г)  .
65. а) .
65. а)  ;
б) ;
б) 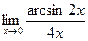 ;
в) ;
в)  ;
г) ;
г)  .
66. а) .
66. а)  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  . .
|
67. а)  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  .
68. а) .
68. а)  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  .
69. а) .
69. а)  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  .
70. а) .
70. а)  ;
б) ;
б) 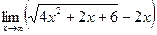 ;
в) ;
в) 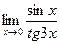 ;
г) ;
г)  . .
| 71. а) 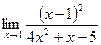 ;
б) ;
б)  в)
в)  ;
г) ;
г)  .
72. а) .
72. а)  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  .
73. а) .
73. а)  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  .
74. а) .
74. а)  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  . .
|
67. а)  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  .
68. а) .
68. а)  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  .
69. а) .
69. а)  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  .
70. а) .
70. а)  ;
б) ;
б) 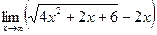 ;
в) ;
в) 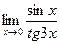 ;
74. а) ;
74. а)  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  .
75. а) .
75. а) 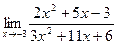 ;
б) ;
б)  ;
в) ;
в) 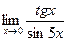 ;
г) ;
г)  ;
76. а) ;
76. а)  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  ;
77. а) ;
77. а)  ;
б) ;
б)  ;
в) ;
в)  ; ;
| г)  .
71. а) .
71. а) 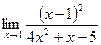 ;
б) ;
б)  в)
в)  ;
г) ;
г)  .
72. а) .
72. а)  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  .
73. а) .
73. а)  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  .
г) .
г)  .
78. а) .
78. а)  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  .
79. а) .
79. а)  ;
б) ;
б) 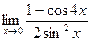 ;
в) ;
в)  ;
г) ;
г) 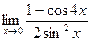 80. а)
80. а)  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  . .
|
Решение типового примера. Найти пределы
а)  . При
. При  и числитель и знаменатель стремятся к нулю (неопределенность
и числитель и знаменатель стремятся к нулю (неопределенность 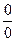 ). Для раскрытия неопределенности разложим многочлен и в числителе и знаменателе на линейные множители и сократим дробь. Получим,
). Для раскрытия неопределенности разложим многочлен и в числителе и знаменателе на линейные множители и сократим дробь. Получим,
 .
.
б)  . При
. При  числитель и знаменатель дроби стремятся к
числитель и знаменатель дроби стремятся к  (неопределенность
(неопределенность 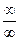 ). Для раскрытия неопределенности разделим числитель и знаменатель на х2 (х2 – самая высокая степень х). Получим,
). Для раскрытия неопределенности разделим числитель и знаменатель на х2 (х2 – самая высокая степень х). Получим,
 .
.
в)  . Для раскрытия неопределенности
. Для раскрытия неопределенности 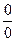 воспользуемся правом замены эквивалентных бесконечно малых сомножителей. В нашем случае
воспользуемся правом замены эквивалентных бесконечно малых сомножителей. В нашем случае  ~3х, sin5x~5х. Поэтому,
~3х, sin5x~5х. Поэтому,  .
.
г)  . Для раскрытия неопределенности
. Для раскрытия неопределенности 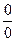 числитель и знаменатель умножим на сопряженную величину
числитель и знаменатель умножим на сопряженную величину 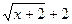 . Получим,
. Получим,
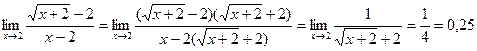 .
.
д)  . Имеем неопределенность вида
. Имеем неопределенность вида  . Для ее раскрытия воспользуемся вторым замечательным пределом:
. Для ее раскрытия воспользуемся вторым замечательным пределом:  Имеем,
Имеем,  . Делаем замену переменной
. Делаем замену переменной  . Тогда
. Тогда 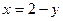 и при
и при  . Получаем,
. Получаем, 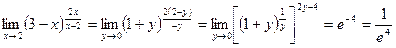 .
.
В задачах 81-100 найти производные  , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
| 81. | а)  , ,
| б)  , ,
| |||
в)  , ,
| г) 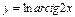 . .
| ||||
| 82. | а)  , ,
| б) 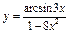 , ,
| |||
в)  , ,
| г)  . .
| ||||
| 83. | а)  , ,
| б)  , ,
| |||
в)  , ,
| г)  . .
| ||||
| 84. | а)  , ,
| б)  , ,
| |||
в)  , ,
| г)  . .
| ||||
| 85. | а)  , ,
| б) 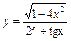 . .
| |||
в)  , ,
| г)  . .
| ||||
| 86. | а)  , ,
| б)  , ,
| |||
в) 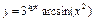 , ,
| г) 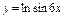 . .
| ||||
| 87. | а)  , ,
| б)  , ,
| |||
в)  , ,
| г)  . .
| ||||
| 88. | а)  , ,
| б)  , ,
| |||
в)  , ,
| г)  . .
| ||||
| 89. | а)  , ,
| б)  , ,
| |||
в) 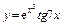 , ,
| г)  . .
| ||||
| 90. | а) 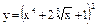 , ,
| б)  . .
| |||
в)  , ,
| г)  . .
| ||||
| 91. | а)  , ,
| б)  , ,
| |||
в)  , ,
| г)  . .
| ||||
| 92. | а)  , ,
| б) 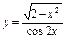 . .
| |||
в)  , ,
| г)  . .
| ||||
| 93. | а)  , ,
| б)  , ,
| |||
в)  , ,
| г)  . .
| ||||
| 94. | а)  , ,
| б)  . .
| |||
в)  , ,
| г)  . .
| ||||
| 95. | а) 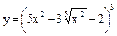 , ,
| б)  , ,
| |||
в)  , ,
| г)  . .
| ||||
| 96. | а)  , ,
| б)  . .
| |||
в)  , ,
| г)  . .
| ||||
| 97. | а)  , ,
| б)  , ,
| |||
в)  , ,
| г)  . .
| ||||
| 98. | а)  , ,
| б)  . .
| |||
в)  , ,
| г)  . .
| ||||
| 99. | а)  , ,
| б) 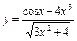 , ,
| |||
в)  , ,
| г)  . .
| ||||
| 100. | а)  , ,
| б)  . .
| |||
в)  , ,
| г)  . .
| ||||
Для нахождения производных надо использовать таблицу производных от основных элементарных функций:  ,
,
а также пользоваться арифметическими свойствами производной (производная от сумы, разности, произведения и частного) и правилом дифференцирования сложной функции 

 . Например, найти производную функции
. Например, найти производную функции  . Данная функция является сложной и имеет вид:
. Данная функция является сложной и имеет вид: 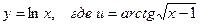 . Поэтому,
. Поэтому, 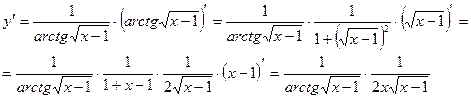
При вычислении производной мы пользовались формулами:
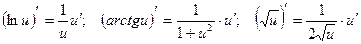 .
.
В ЗАДАЧАХ 101-120 исследовать заданные функции методами дифференциального исчисления, начертить их графики. Исследование функций и построение графиков рекомендуется проводить по следующей схеме:
1) найти область определения функции D (y);
2) исследовать функцию на непрерывность; найти точки разрыва функции и ее односторонние пределы в точках разрыва;
3) найти точки экстремума функции и определить интервалы ее монотонности;
4) найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика;
5) найти асимптоты графика функции;
6) построить график, используя результаты предыдущих исследований;
| 101. |  . .
| 111. | |||
 . .
| |||||
| 102. | 112. | ||||
 . .
|  . .
| ||||
| 103. | 113. | ||||
 . .
|  . .
| ||||
| 104. | |||||
 . .
|  . .
| ||||
| 105. | 115. | ||||
 . .
|  . .
| ||||
| 106. | 116. | ||||
 . .
|  . .
| ||||
| 107. | 117. | ||||
 . .
|  . .
| ||||
| 108. | 118. | ||||
 . .
|  . .
| ||||
| 109. | 119. | ||||
 . .
|  . .
| ||||
| 110. | 120. | ||||
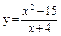 . .
| 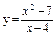 . .
| ||||
Решение типового примера.
Методами дифференциального исчисления исследовать функцию  и построить ее график.
и построить ее график.
1) Область определения функции – те значения х, при которых знаменатель отличен от нуля, т.е.  .
.
2) Функция имеет разрыв второго рода в точке  . При этом
. При этом  ;
; 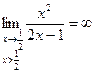
 . Поэтому прямая
. Поэтому прямая  является вертикальной асимптотой функции.
является вертикальной асимптотой функции.
3) Для нахождения интервалов монотонности и точек экстремума найдем производную и точки, в которых она равна нулю или не существует (критические точки). 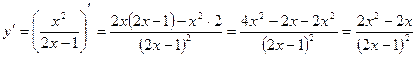 . Производная равна нулю, если
. Производная равна нулю, если 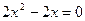 , т.е.
, т.е.  . Таким образом, точки
. Таким образом, точки  разбивают область определения на четыре интервала:
разбивают область определения на четыре интервала:  . Для определения характера монотонности на полученных интервалах, найдем знак производной
. Для определения характера монотонности на полученных интервалах, найдем знак производной  из приведенной схемы видим, что
из приведенной схемы видим, что 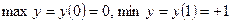 .
.
4) Для нахождения интервалов выпуклости и вогнутости найдем производную второго порядка и точки, где она равна нулю или не существует (критические точки второго рода). Имеем,  Так как
Так как 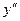 существует в каждой точке области определения и не обращается в нуль, то точек перегиба нет. На интервале
существует в каждой точке области определения и не обращается в нуль, то точек перегиба нет. На интервале  и функция выпукла, на интервале
и функция выпукла, на интервале  и функция вогнута.
и функция вогнута.
5) В п.1 мы нашли вертикальную асимптоту  . Найдем теперь не вертикальные асимптоты
. Найдем теперь не вертикальные асимптоты  , где
, где  . Имеем,
. Имеем,  .
.  . Невертикальной будет асимптота
. Невертикальной будет асимптота  .
.
6) По данным исследования построим график функции
Поиск по сайту: