Контрольная работа № 2. В ЗАДАЧАХ 141-160 найти неопределенные интегралы способом подстановки (методом замены переменной). 141. . 148. . 155

В ЗАДАЧАХ 141-160 найти неопределенные интегралы способом подстановки (методом замены переменной).

141.	.	148.	.	155.	.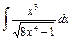
142.	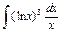.	149.	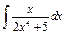.	156.	.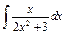
143.	.	150.	.	157.	.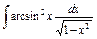
144.	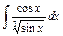.	151.	.	158.	.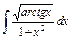
145.	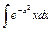.	152.	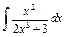.	159.	.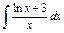
146.	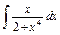.	153.	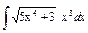.	160.	.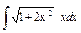
147.	.	154.	.

Решение типовых примеров.

Найти неопределенные интегралы:

1. 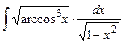. Сделаем замену t=arccosx. Тогда 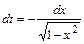и .

2. 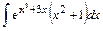. Применим подстановку , тогда , откуда .

В задачах 161-180 найти неопределенные интегралы, используя выделение полного квадрата.

161.	.	168.	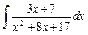.	175.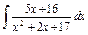
162.	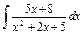.	169.	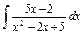.	176.
163.	.	170.	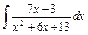.	177.
164.	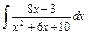.	171.	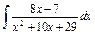.	178.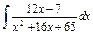
165.	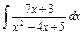.	172.	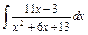.	179.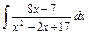
166.	.	173.	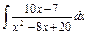.	180.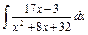
167.	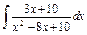.	174.	.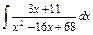

Решение типового примера. Найти интеграл

.

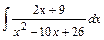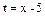Решение: преобразуем знаменатель дроби, стоящий под знаком интеграла следующим образом: . Тогда после замены , получаем:

; второй интеграл является табличным.

Для решения первого интеграла нужно воспользоваться заменой переменной: 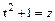, тогда 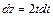, откуда 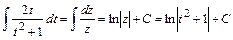. Таким образом окончательный ответ 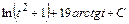или .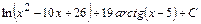

В ЗАДАЧАХ 181-200 найти неопределенные интегралы, применяя метод интегрирования по частям.

181.	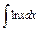.	188.	.	195.	.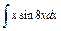
182.	.	189.	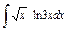.	196.	.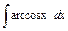
183.	.	190.	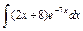.	197.	.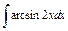
184.		191.	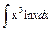.	198.	.
185.	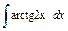.	192.	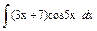.	199.	.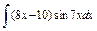
186.	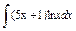.	193.	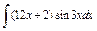.	200.	.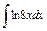
187.	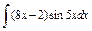.	194.	.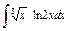

Решение типового примера.

Найти интеграл:

1.

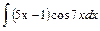
Решение: применим формулу интегрирования по частям 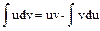. Разбиваем подитегральное выражение на части: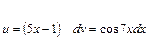

тогда .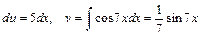

Следовательно, .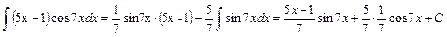

2.

Решение: положим 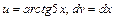, тогда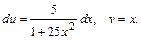

Отсюда 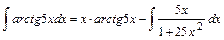. Применяя в последнем интеграле подстановку 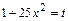, получаем , следовательно, ,

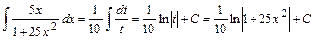отсюда .

В ЗАДАЧАХ 201-220 найти неопределенные интегралы, пользуясь разложением рациональных дробей на сумму простейших.

201.	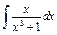.	208.	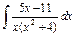.	215.	.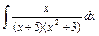
202.	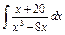.	209.	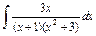.	216.	.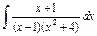
203.	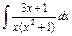.	210.	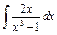.	217.	.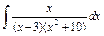
204.	.	211.	.	218.	.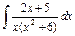
205.	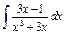.	212.	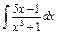.	219.	.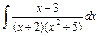
206.	.	213.	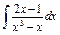.	220.	.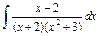
207.	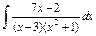.	214.	.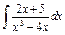

Решение типового примера.

Найти интеграл

Решение: разложим знаменатель на множители: ,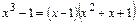

тогда освобождаемся от знаменателя: .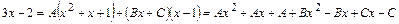

Теперь приравниваем коэффициенты при одинаковых степенях х:

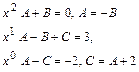
Из второго уравнения получаем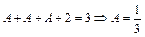

Отсюда .

Следовательно, .

Выделим полный квадрат в знаменателе подинтегрального выражения:

.

Произведем подстановку и

Ответ: .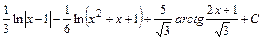

В ЗАДАЧАХ 221-240 вычислить площадь, ограниченную заданными параболами.

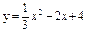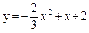
221.	;	228.	;	235.	;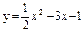
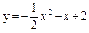
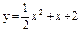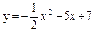
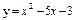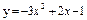
222.	;	229.	;	236.	;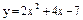
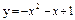
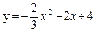
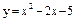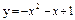
223.	;	230.	;	237.	;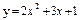
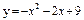
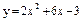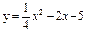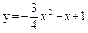
224.	;	231.	;	238.	;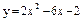
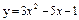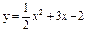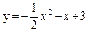
225.	;	232.	;	239.	;
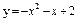
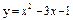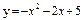
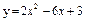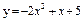
226.	;	233.	;	240.	;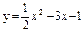
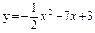
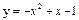
227.	;	234.	;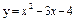

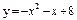
Решение типового примера. Вычислим площадь фигуры, ограниченной параболами

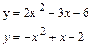
Решение: найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений:

отсюда

Вычисление площади осуществляется по формуле

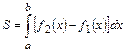, где 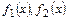- кривые, ограничивающие фигуру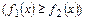

В нашем случае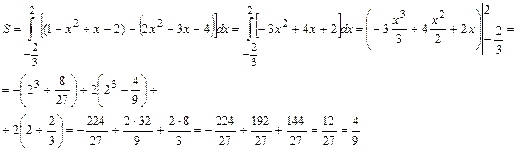

В задачах 241-260 найти объем тела, образованного вращением вокруг оси Ох фигуры, расположенной в первом квадрате и ограниченной заданными параболой и прямой.

241.	;	248.	;	255.	;
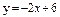
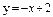
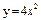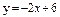
242.	;	249.	;	256.	;
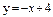
243.	;	250.	;	257.	;
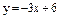
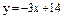
244.	;	251.	;	258.	;
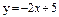
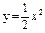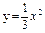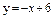
245.	;	252.	;	259.	;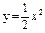
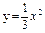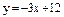
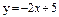
246.	;	253.	;	260.	;
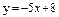
247.	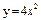;	254.	;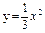

Решение типового примера.

Найти объем тела, образованного вращением вокруг оси Ох фигуры, расположенной в первом квадранте и ограниченной параболой 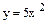, прямой 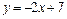и ось Ох.

Решение: найдем абсциссу точки пересечения параболы и прямой в первом квадранте из системы уравнений 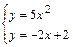, откуда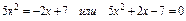

Для этого решим уравнение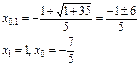

А также, найдем абсциссу точки пересечения прямой с осью Ох:

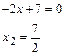
Тогда, используя формулу для вычисления объема тела вращения, получим:

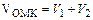, где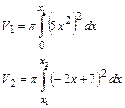

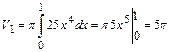
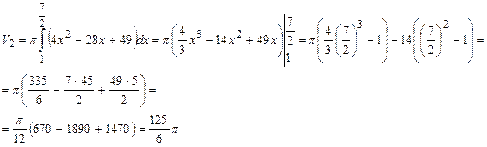
В ЗАДАЧАХ 261 – 280 найти частное решение дифференциального уравнения, удовлетворяющее указанному начальному условию.

261.

262.

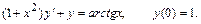
263.

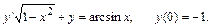
264.

265.

266.

267.

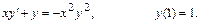
268.

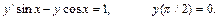
269.

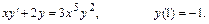
270.

271.

272.

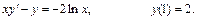
273.

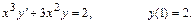
274.

275.

276.

277.

278.

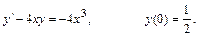
279.

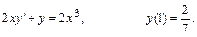
280.

Решение типового примера. Найти частное решение дифференциального уравнения , удовлетворяющее данному условию у(1)=е.

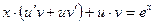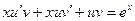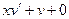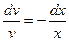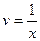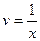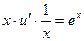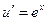Решение. Данное уравнение является линейным и его можно решить с помощью подстановки Бернулли. Положим, y=uv. Тогда . Подставим в исходное уравнение. Получим, или или . Потребуем, чтобы выполнялось равенство , т.е. или или, после интегрирования , т.е. . Для найденного уравнение примет вид или т.е. 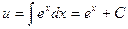. Значит, общим решением уравнения будет . Подставляя заданное начальное условие у(1)=е, получим e=е+C. Откуда С=0 и нужным частным решением будет .

Поиск по сайту: