Определение тесноты и существенности связи

Эмпирическая линия регрессии (рис. 1) – ломаная линия. Изломы этой линии свидетельствуют о влиянии на признак «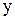» прочих факторов, помимо признака «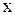». Чтобы абстрагироваться от влияния прочих факторов, нужно прибегнуть к выравниванию полученной ломаной линии регрессии. Для этого сначала необходимо установить теоретическую форму связи, т.е. выбрать определенный вид функции, наилучшим образом отображающий характер изучаемой связи.

Выбор формы связи имеет решающее значение в корреляционно-регрессионном анализе, но этот выбор всегда связан с некоторой условностью, вызванный тем, что нужно находить форму функциональной зависимости, в то время как зависимость лишь в той или иной степени приближается к функциональной. Но если зависимость довольно высокая, т.е. довольно близко приближается к функциональной, тогда именно теоретическая линия регрессии и ее параметры приобретают практическое значение.

На основании качественного анализа исходных данных (табл.2) и эмпирической линии регрессии (рис.1) можно предположить, что между ОПФ и прибылью предприятий существует линейная зависимость. Для определения тесноты этой зависимости воспользуемся линейным коэффициентом корреляции:

,

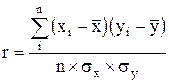где		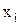значение факторного показателя;
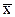
		среднее значение факторного показателя;
		значение результативного показателя;
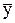
		среднее значение результативного показателя;
		число единиц в совокупности;
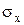
		среднее квадратическое отклонение по факторному показателю;
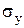
		среднее квадратическое отклонение по результативному показателю;

Для вычисления линейного коэффициента корреляции воспользуемся расчетами, выполненными в табл. 3, тогда

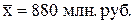
Среднее значение и среднее квадратическое отклонение результативного показателя рассчитывается аналогично факторному:

; ,

где		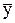среднее значение результативного показателя;
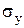
		среднее квадратическое отклонение по результативному показателю;
		значение результативного показателя;
		число единиц в совокупности;

.

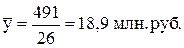
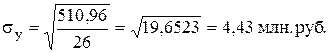
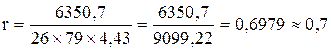Коэффициент корреляции показывает не только тесноту, но и направление связи. Его значение изменяется от до . Если коэффициент имеет знак минус, значит, связь обратная, если имеет знак плюс, то связь прямая. Близость к единице в том и в другом случае характеризует близость к функциональной зависимости.

Таким образом, значение 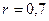свидетельствует о прямой и достаточно тесной связи между величиной ОПФ и прибылью предприятия.

Однако, чтобы это утверждать, необходимо дать оценку существенности линейного коэффициента корреляции, что можно выполнить на основании расчета t -критерия Стьюдента:

,

где		линейный коэффициент корреляции;
		число единиц в совокупности.

.

Для числа степеней свободы и уровня значимости 1% табличное значение 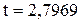, т.е. . Следовательно, с вероятностью можно утверждать, что в генеральной совокупности существует достаточно тесная прямая линейная зависимость между величиной ОПФ и прибылью предприятия.

Поиск по сайту: