 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ИНТЕГРАЛДАР КЕСТЕСІ
|
Читайте также: |
 = C
= C 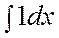 = x + C
= x + C  =
=  + C, x>0,
+ C, x>0, 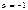
 = ln| x |+ C, x
= ln| x |+ C, x  0
0  =
= 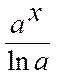 + C,
+ C, 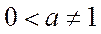
 =
=  + C
+ C  = sinx + C
= sinx + C
 =- cosx + C
=- cosx + C  = tgx + C,
= tgx + C, 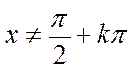
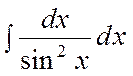 =- ctgx + C,
=- ctgx + C, 
 = arcsinx + C, -1<x<1
= arcsinx + C, -1<x<1  = arctgx + C
= arctgx + C  =
=  artg
artg  + C
+ C
 =
=  ln
ln  + C
+ C  ln
ln 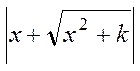 +C
+C
33. Айнымалыларды алмастыру және бөліктеп интегралдау әдісі.
I=  интегралын қарастырайық. Айталық, x=g(t) дифференциалданатын функция болсын. Сонда dx=g’(t)dt және
интегралын қарастырайық. Айталық, x=g(t) дифференциалданатын функция болсын. Сонда dx=g’(t)dt және 
 . Бұләдіс айнымалыны ұтымды алмастыруға негізделген. Айнымалыны алмастыру арқылы интегралды бірден немесе бірнеше амалдардан кейін кестелік интегралға келтіріледі. Мысалдар қарастырайық.
. Бұләдіс айнымалыны ұтымды алмастыруға негізделген. Айнымалыны алмастыру арқылы интегралды бірден немесе бірнеше амалдардан кейін кестелік интегралға келтіріледі. Мысалдар қарастырайық.



 +С
+С 

 arctgt+C= =
arctgt+C= =  arctgx3+C
arctgx3+C
В 
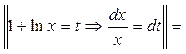
 ln|t|+C=ln|1+lnx|+с. Бөліктеп интегралдау әдісі. Бұл әдіс мынадай қатынасқа негізделген: d(uv) = udv + vdu
ln|t|+C=ln|1+lnx|+с. Бөліктеп интегралдау әдісі. Бұл әдіс мынадай қатынасқа негізделген: d(uv) = udv + vdu  udv = d(uv) – vdu
udv = d(uv) – vdu
мұндағы u=f(x) және v=g(x) функциялары туындылары бар функциялар. Теңдіктің екі жағынан да интеграл алсақ, 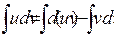 , осыдан
, осыдан  .Бұл әдісті қолданғанда u және v функцияларын
.Бұл әдісті қолданғанда u және v функцияларын  интеграл
интеграл  интегралға қарағанда оңай алынатындай етіп таңдайды. Мысалдар қарастырайық. а)
интегралға қарағанда оңай алынатындай етіп таңдайды. Мысалдар қарастырайық. а) 

 +С =
+С =  +C.б)
+C.б) 


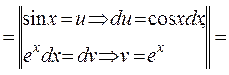

 . J=
. J=  (cosx+sinx)-J
(cosx+sinx)-J  J=
J= 
 (cosx+sinx)+C. Төмендегі интегралдар тобы тек бөліктеп интегралдау әдісімен есептелінеді:
(cosx+sinx)+C. Төмендегі интегралдар тобы тек бөліктеп интегралдау әдісімен есептелінеді:  ;
;  ;
;  ;
;  .
.
34. Қарапайым рационал функцияларды интегралдау
 түріндегі өрнекті n– дәрежелі көпмүшелік деп атайды. Мұндағы
түріндегі өрнекті n– дәрежелі көпмүшелік деп атайды. Мұндағы  - нақты сандар (
- нақты сандар ( , n >0). Көпмүшеліктердің қатынасы түрінде берілген өрнек рационал өрнек болады. Мысалы
, n >0). Көпмүшеліктердің қатынасы түрінде берілген өрнек рационал өрнек болады. Мысалы 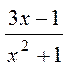 , бөлшектер раци
, бөлшектер раци  онал өрнектер. Егер бөлшектің алымындағы көпмүшеліктің дәрежесі бөліміндегі көпмүшелік дәрежесінен кем болса, бөлшек дұрыс деп, ал кем болмаса бөлшек бұрыс деп аталады. Мысалдағы біріншісі бөлшек - дұрыс, ал екіншісі – бұрыс бөлшек. Кез келген бұрыс бөлшекті алымын бөлімге бөлу арқылы дұрыс бөлшекке келтіріп алуға болады. Мысалы,
онал өрнектер. Егер бөлшектің алымындағы көпмүшеліктің дәрежесі бөліміндегі көпмүшелік дәрежесінен кем болса, бөлшек дұрыс деп, ал кем болмаса бөлшек бұрыс деп аталады. Мысалдағы біріншісі бөлшек - дұрыс, ал екіншісі – бұрыс бөлшек. Кез келген бұрыс бөлшекті алымын бөлімге бөлу арқылы дұрыс бөлшекке келтіріп алуға болады. Мысалы,  бөлшекті дұрыс бөлшекке келтірейік:
бөлшекті дұрыс бөлшекке келтірейік:  Сонымен, берілген бөлшектің бүтін бөлігін бөліп дұрыс бөлшекке келтірдік:
Сонымен, берілген бөлшектің бүтін бөлігін бөліп дұрыс бөлшекке келтірдік:  .Мектеп курсынан көпмүшеліктің мынадай қасиеті белгілі: Кез келген көпмүшелікті
.Мектеп курсынан көпмүшеліктің мынадай қасиеті белгілі: Кез келген көпмүшелікті  және
және  түріндегі көбейткіштерге жіктеуге болады. Мынадай тұжырым дұрыс болады: Егер дұрыс рационал бөлшек бөлімі
түріндегі көбейткіштерге жіктеуге болады. Мынадай тұжырым дұрыс болады: Егер дұрыс рационал бөлшек бөлімі  және
және  түріндегі көбейткіштерге жіктелген болса, ондабөлшектімынадай қарапайым бөлшектердің қосындысына жіктеуге болады:
түріндегі көбейткіштерге жіктелген болса, ондабөлшектімынадай қарапайым бөлшектердің қосындысына жіктеуге болады: 

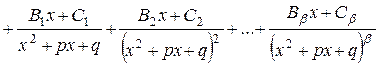 , мұндағы, Р(х) – белгілі көпмүшелік,
, мұндағы, Р(х) – белгілі көпмүшелік, 

 - белгісіз коэффициенттер. Ол коэффициенттерді табу үшін белгісіз коэффициенттер әдісін пайдаланамыз: теңдіктің оң жағын ортақ бөлімге келтіреміз; екі бөлшектің бөлімдері тең болатындықтан, алымдарын теңестіреміз; теңдіктің екі жағындағы х айнымалының бірдей дәрежелері алдындағы коэффициенттерін теңестіру арқылы теңдеулер жүйесін аламыз; осы жүйені шешіп белгісіз коэффициенттерді табамыз. Мысалы
- белгісіз коэффициенттер. Ол коэффициенттерді табу үшін белгісіз коэффициенттер әдісін пайдаланамыз: теңдіктің оң жағын ортақ бөлімге келтіреміз; екі бөлшектің бөлімдері тең болатындықтан, алымдарын теңестіреміз; теңдіктің екі жағындағы х айнымалының бірдей дәрежелері алдындағы коэффициенттерін теңестіру арқылы теңдеулер жүйесін аламыз; осы жүйені шешіп белгісіз коэффициенттерді табамыз. Мысалы  бөлшегін қарапайым бөлшектер қосындысына жіктейік Бөлшек дұрыс, сондықтан (2) формула бойынша бөлшекті жіктейміз,
бөлшегін қарапайым бөлшектер қосындысына жіктейік Бөлшек дұрыс, сондықтан (2) формула бойынша бөлшекті жіктейміз,  Белгісіз коэффициенттерді табу үшін теңдіктің оң жағын ортақ бөлімге келтіріп жазайық:
Белгісіз коэффициенттерді табу үшін теңдіктің оң жағын ортақ бөлімге келтіріп жазайық:  .Теңдіктің екі жағындағы х айнымалының бірдей дәрежелері алдындағы коэффициенттерін теңестіру арқылы теңдеулер жүйесін аламыз:
.Теңдіктің екі жағындағы х айнымалының бірдей дәрежелері алдындағы коэффициенттерін теңестіру арқылы теңдеулер жүйесін аламыз:  Төрт белгісізді, төрт теңдеуден тұрған жүйені шешіп, белгісіз коэффициенттерді табамыз:
Төрт белгісізді, төрт теңдеуден тұрған жүйені шешіп, белгісіз коэффициенттерді табамыз:  .Табылған мәндерді теңдіктегі орнына қойып, бөлшектің қарапайым жіктелуін аламыз:
.Табылған мәндерді теңдіктегі орнына қойып, бөлшектің қарапайым жіктелуін аламыз:  . Енді осы рационал бөлшекті интегралдайық.
. Енді осы рационал бөлшекті интегралдайық. 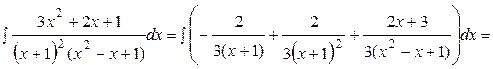
 Әр интегралды жеке қарастырайық. 1)
Әр интегралды жеке қарастырайық. 1) 
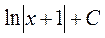 , мұнда бөлшектің алымы бөлімінің туындысы болғандықтан 7-қасиетті пайдаландық. 2)
, мұнда бөлшектің алымы бөлімінің туындысы болғандықтан 7-қасиетті пайдаландық. 2) 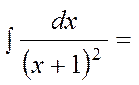

 + С=
+ С= 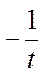 +C=
+C=  +C; 3)
+C; 3) 


 +4=
+4=  +
+  +C, мұнда бірінші қосылғышты алымы бөлімінің туындысы болғандай етіп түрлендірдік те 7-қасиетті пайдаландық. Ал екінші қосылғышта бөлімінің толық квадратын бөліп алып, интегралдар кестесіндегі 14-формуланы пайдаландық. Сонымен,
+C, мұнда бірінші қосылғышты алымы бөлімінің туындысы болғандай етіп түрлендірдік те 7-қасиетті пайдаландық. Ал екінші қосылғышта бөлімінің толық квадратын бөліп алып, интегралдар кестесіндегі 14-формуланы пайдаландық. Сонымен, 
 ln| x+1 |-
ln| x+1 |- 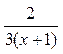

 +
+  +C.
+C.
35. Ньютон - Лейбниц формуласы. Меншіксіз интеграл
Ньютон-Лейбниц формуласы. 
 F(b) – F(a), мұндағы
F(b) – F(a), мұндағы  .
.
1. Меншіксіз интеграл. Егер y=f(x) функциясы  аралығында үзіліссіз болса, онда мына шекті
аралығында үзіліссіз болса, онда мына шекті 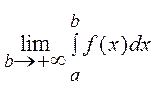 жоғары шегі шексіз меншіксіз интеграл дейді және былай жазады:
жоғары шегі шексіз меншіксіз интеграл дейді және былай жазады:

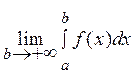 .
.
Теңдіктің оң жағындағы шек ақырлы болса меншіксіз интеграл жинақталады деп, ал шек ақырсыз немесе болмаса меншіксіз интеграл жинақталмайды дейді. Осыған ұқсас мынадай меншіксіз интегралдар анықталады:

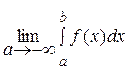 ,
, 
 .
.
37. Көп айнымалыдан тәуелді ф-ия. Анықталу обл. Деңгейлік сызықтар
Өмірде қандай да бір құбылыстар, оның ішінде экономикалық қатынастар да, бірнеше шамалардың байланысы арқылы сипатталады. Осы байланыстарды зерттеу көп айнымалы функция ұғымын енгізуді қажет етеді. Анықтама. Қандай да бір Х жиынының  элементтеріне қандай да бір заң немесе ереже бойынша z шама сәйкес қойылса, Х жиынында п айнымалыдан тәуелді функция берілген дейміз де z=
элементтеріне қандай да бір заң немесе ереже бойынша z шама сәйкес қойылса, Х жиынында п айнымалыдан тәуелді функция берілген дейміз де z=  деп жазамыз. Мұндағы
деп жазамыз. Мұндағы 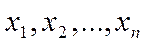 айнымалылар тәуелсіз айнымалы немесе аргумент, ал z тәуелді айнымалы немесе функция, f – заң немесе ереже, ал Х - функцияның анықталу облысы болады.
айнымалылар тәуелсіз айнымалы немесе аргумент, ал z тәуелді айнымалы немесе функция, f – заң немесе ереже, ал Х - функцияның анықталу облысы болады.
Бұдан былайғы жағдайда екі айнымалыдан тәуелді функция қарастырамыз. Екі айнымалыдан тәуелді функцияға қатысты айтылған тұжырымдардың барлығын одан да жоғарғы айнымалыдан тәуелді функциялар үшін дұрыс болады.
 Екі айнымалыдан тәуелді функцияны
Екі айнымалыдан тәуелді функцияны
z= 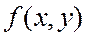
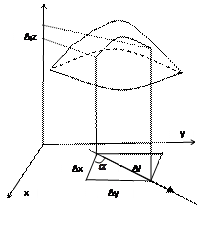
деп белгілейміз. Бұл функцияның анықталу облысы хОу жазықтығында анықталады. Екі айнымалы дан тәуелді функция графигі үш өлшемді кеңістіктегі (х, у, z) нүктелердің геометриялық орнымен анықталатын қандай да бір бет болады. Мұнда х – абсцисса, у – ордината, z – апликата, және олар арасында z = f(x, y) функциялық байланыс бар.
Функция графигін z = С жазықтығымен қиғанда пайда болатын сызық z= f(x, y) функциясының деңгейлік сызығы деп аталады: f(x, y) = С (2)
Көп жағдайда функция графигін қарастырғаннан гөрі оның деңгейлік сызығын зерттеу оңай болады.
z= f(x, y) функциясына бір айнымалыдан тәуелді екі функция сәйкес қоюға болады: х аргументті тұрақты деп (x=x0) қарастырғанда z= f(x0 , y) функциясын және у аргументті тұрақты деп (у=у0) қарастырғанда z= f(x, y0) функциясын.
38. Дербес туынды.Толық дифференциал.
z= f(x, y) функциясын қарастырайық. х аргументке  х өсімше у аргументке
х өсімше у аргументке  у өсімше берсек функция жаңа мәнге ие болады, z= f(x+
у өсімше берсек функция жаңа мәнге ие болады, z= f(x+  х, y+
х, y+ 
 z= f(x+
z= f(x+  х, y+
х, y+  у ) – f(x, y) шамасы функцияның (х,у) нүктедегі толық өсімшесі деп аталады. Егер тек х не у аргументке ғана өсімше берсек, онда функцияның сәйкес дербес өсімшелерін аламыз
у ) – f(x, y) шамасы функцияның (х,у) нүктедегі толық өсімшесі деп аталады. Егер тек х не у аргументке ғана өсімше берсек, онда функцияның сәйкес дербес өсімшелерін аламыз
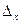 z= f(x+
z= f(x+  х, y) – f(x, y);
х, y) – f(x, y);  z= f(x, y+
z= f(x, y+  у ) – f(x, y) А-ма. Z= f(x, y) функциясының дербес өсімшелерінің сәйкес аргумент өсімшесіне қатынасының аргумент өсімшесі нолге ұмтылған жағдайдағы шегі функцияның дербес туындысы деп аталады және былайша жазылады:
у ) – f(x, y) А-ма. Z= f(x, y) функциясының дербес өсімшелерінің сәйкес аргумент өсімшесіне қатынасының аргумент өсімшесі нолге ұмтылған жағдайдағы шегі функцияның дербес туындысы деп аталады және былайша жазылады: 
 Бұл анықтамадан
Бұл анықтамадан 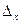 z туындыны табу үшін у айнымалыны тұрақты деп, ал
z туындыны табу үшін у айнымалыны тұрақты деп, ал  z туындыны табу үшін х айнымалыны тұрақты деп қарастыру керек. Және де бір айнымалы функция дифференциалынан белгілі дифференциалдаудың барлық ережелері сақталады. Мысал.
z туындыны табу үшін х айнымалыны тұрақты деп қарастыру керек. Және де бір айнымалы функция дифференциалынан белгілі дифференциалдаудың барлық ережелері сақталады. Мысал.  функциясының дербес туындыларын табу керек. Шешуі. x бойынша дербес туындыны табу үшін у айнымалыны тұрақты деп аламыз, сонда
функциясының дербес туындыларын табу керек. Шешуі. x бойынша дербес туындыны табу үшін у айнымалыны тұрақты деп аламыз, сонда  . у бойынша дербес туындыны табу үшін х айнымалыны тұрақты деп аламыз, сонда
. у бойынша дербес туындыны табу үшін х айнымалыны тұрақты деп аламыз, сонда  . Егер
. Егер  және
және  дербес туындылар дифференциалданатын функциялар болса, онда бұл функциялардың екінші ретті дербес туындыларын табуға болады.
дербес туындылар дифференциалданатын функциялар болса, онда бұл функциялардың екінші ретті дербес туындыларын табуға болады.  функциясының дербес туындыларын табсақ
функциясының дербес туындыларын табсақ  ,
,  .
.  функциясының дербес туындыларын табсақ
функциясының дербес туындыларын табсақ  ,
,  . Функцияның екінші ретті
. Функцияның екінші ретті  және
және  дербес туындыларын функцияның аралас туындылары деп атайды. Егер z= f(x, y) функциясы мен оның аралас туындылары қандай да бір М(х0,у0) нүктенің маңайында анықталған және үзіліссіз болса, онда функцияның аралас туындылары өзара тең болады,
дербес туындыларын функцияның аралас туындылары деп атайды. Егер z= f(x, y) функциясы мен оның аралас туындылары қандай да бір М(х0,у0) нүктенің маңайында анықталған және үзіліссіз болса, онда функцияның аралас туындылары өзара тең болады, 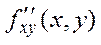 =
=  Мысал.
Мысал.  функциясының екінші ретті дербес туындыларын табу керек. Шешуі. Бірінші ретті дербес туындылары алдыңғы мысалда табылған:
функциясының екінші ретті дербес туындыларын табу керек. Шешуі. Бірінші ретті дербес туындылары алдыңғы мысалда табылған:  ,
,  Енді осы туындылардан туынды табайық.
Енді осы туындылардан туынды табайық.  ,
, 
 ,
,  А-ма. z= f(x, y) функцияның толық дифференциалы деп осы функцияның дербес туындыларының сәйкес аргумент өсімшелеріне көбейтіндісінің қосындысын айтамыз,
А-ма. z= f(x, y) функцияның толық дифференциалы деп осы функцияның дербес туындыларының сәйкес аргумент өсімшелеріне көбейтіндісінің қосындысын айтамыз,  (*) Егер f(x,y) = x, g(x,y) = y функциялары үшін (*) қатынас бойынша толық дифференциалдарын тапсақ, df = dx=
(*) Егер f(x,y) = x, g(x,y) = y функциялары үшін (*) қатынас бойынша толық дифференциалдарын тапсақ, df = dx=  x, dg = dy=
x, dg = dy=  y болатындығы шығады. Олай болса функцияның толық дифференциалын мына түрде жазуға болады:
y болатындығы шығады. Олай болса функцияның толық дифференциалын мына түрде жазуға болады: 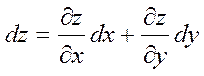 .
.
39. Бағыт бойынша туынды ж-е градиент
z= f(x, y) функциясы М(х,у) нүктесінің қандай да бір маңайында анықталған болсын және  вектор бағытымен анықталатын қандай да бір l бағыт берілсін. Мұнда
вектор бағытымен анықталатын қандай да бір l бағыт берілсін. Мұнда  және
және  бұрыштар
бұрыштар  векторының Ох және Оу осімен жасайтын бұрышы, ал
векторының Ох және Оу осімен жасайтын бұрышы, ал  - вектордың бағыттаушы косинустары деп аталады және
- вектордың бағыттаушы косинустары деп аталады және
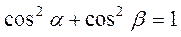 ,
,  .
.
М(х,у) нүктесі l бағыт бойымен қозғалып М1(х+  х, у+
х, у+  у) нүктеге өзгергенде z функция
у) нүктеге өзгергенде z функция
 z = f(х+
z = f(х+  х, у+
х, у+  у) - f(x, y)
у) - f(x, y)
 өсімше алады. Егер ММ1 =
өсімше алады. Егер ММ1 =  l болса, онда
l болса, онда  х=
х=  lcos
lcos  ,
,  y=
y=  lcos
lcos  , олай болса
, олай болса
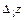 =
=
f(х+  lcos
lcos  , у+
, у+  lcos
lcos  ) - f(x, y).
) - f(x, y).
|
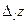 өсімшесінің
өсімшесінің  l шамаға қатынасының осы шама нолге ұмтылғандағы шегі функцияның бағыт бойынша туындысы деп аталады, яғни
l шамаға қатынасының осы шама нолге ұмтылғандағы шегі функцияның бағыт бойынша туындысы деп аталады, яғни
 .
.
Функцияның бағыт бойынша туындысының абсолют шамасы функция өзгеруінің жылдамдығын анықтайды, ал таңбасы функция өзгерісін («+» - өсетінін, «-» - кемитінін) сипаттайды.
z= f(x, y) функциясының  және
және  дербес туындылары функцияның Ох және Оу остеріне параллель бағыт бойынша алынған туындылары болады.
дербес туындылары функцияның Ох және Оу остеріне параллель бағыт бойынша алынған туындылары болады.
Бағыт бойынша туынды анықтамасынан

 cos
cos  +
+  cos
cos  (7)
(7)
болатындығы шығады.
Егер l бағыт координаталарымен берілсе, яғни  , онда бұл вектордың бағыттаушы косинустары былайша табылады:
, онда бұл вектордың бағыттаушы косинустары былайша табылады:
cos  =
= 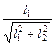 , cos
, cos  =
=  (8).
(8).
Анықтама. z= f(x, y) функциясының градиенті деп координаталары ( ,
,  )болатын векторды айтады және grad z деп белгілейді,
)болатын векторды айтады және grad z деп белгілейді,
grad z= ( ,
,  ) (9)
) (9)
(7) формуланың оң жағында grad z = ( ,
,  ) векторы мен
) векторы мен 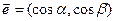 векторының скаляр көбейтіндісі тұр, олай болса бағыт бойынша туынды дегеніміз градиент пен бағытты анықтайтын бірлік вектордың скаляр көбейтіндісіне тең екен:
векторының скаляр көбейтіндісі тұр, олай болса бағыт бойынша туынды дегеніміз градиент пен бағытты анықтайтын бірлік вектордың скаляр көбейтіндісіне тең екен:
 (grad z,
(grad z,  ) (10)
) (10)
Екі вектор бірдей бағытталғанда олардың скаляр көбейтіндісі ең үлкен мән қабылдайды. Олай болса grad z функцияның нүктедегі максималды жылдамдық (өсу) бағытын көрсетеді екен.
Мынадай тұжырым дұрыс болады: Қандай да бір М(х0,у0) нүктеде дифференциалданатын z= f(x, y) функциясының градиенті сол нүкте арқылы өтетін деңгейлік сызыққа перпендикуляр болады.
Мысал.  функциясының А(-3; 2) нүктедегі градиенті мен
функциясының А(-3; 2) нүктедегі градиенті мен  векторы бағытындағы туындысын табу керек.
векторы бағытындағы туындысын табу керек.
Шешуі. Алдымен дербес туындылар табамыз:
 ,
,  .
.
Дербес туындылардың А нүктесіндегі мәнін есептейміз:
 ,
, 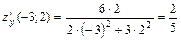
(9) формула бойынша функцияның А нүктесіндегі градиенті
grad z =  табылды.
табылды.
Енді осы нүктедегі бағыт бойынша туындыны табайық. (8) формула бойынша вектордың бағыттаушы косинустарды табамыз:
cos  =
=  , cos
, cos  =
=  .
.
(7) формула бойынша функцияның А нүктесіндегі  векторы бағытындағы туындыны табылды
векторы бағытындағы туындыны табылды

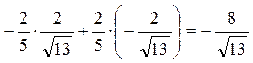
40. Екі айнымалыдан тәуелді функция экстремумы, қажетті және жеткілікті шарттары
Екі айнымалыдан тәуелді z= f(x, y) функциясын қарастырайық. М(х0,у0) нүктесі функцияның анықталу облысына тиісті нүкте болсын. А-ма. М(х0,у0) нүктенің жақын маңайында жатқан барлық (х, у) нүктелер үшін f(х0,у0) 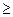 f(x,y) теңсіздігі орындалса, М(х0,у0) функцияның максимум нүктесі деп, ал f(х0,у0)
f(x,y) теңсіздігі орындалса, М(х0,у0) функцияның максимум нүктесі деп, ал f(х0,у0) 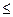 f(x,y) теңсіздігі орындалса, М(х0,у0) функцияның минимум нүктесі деп аталады. Функция максимумы мен минимумы функция экстремумы деп аталады. Экстремумның қажетті шарты. М(х0,у0) нүктесі z= f(x, y) функциясының экстремум нүктесі болса, онда бұл нүктедегі функцияның дербес туындылары нолге тең,
f(x,y) теңсіздігі орындалса, М(х0,у0) функцияның минимум нүктесі деп аталады. Функция максимумы мен минимумы функция экстремумы деп аталады. Экстремумның қажетті шарты. М(х0,у0) нүктесі z= f(x, y) функциясының экстремум нүктесі болса, онда бұл нүктедегі функцияның дербес туындылары нолге тең,  ,
,  . Экстремумның жеткілікті шарты. z= f(x, y) функциясы: 1) дербес туындылары нолге тең болатын
. Экстремумның жеткілікті шарты. z= f(x, y) функциясы: 1) дербес туындылары нолге тең болатын  ,
,  , М(х0,у0) нүктесінің маңайында анықталған болсын; 2) функцияның осы нүктеде екінші ретті үзіліссіз туындылары бар,
, М(х0,у0) нүктесінің маңайында анықталған болсын; 2) функцияның осы нүктеде екінші ретті үзіліссіз туындылары бар,  ,
, 
 ,
,  . Онда, егер
. Онда, егер  болса М(х0,у0) нүктеде экстремум бар, және егер A<0 – максимум, A>0 – минимум; ал
болса М(х0,у0) нүктеде экстремум бар, және егер A<0 – максимум, A>0 – минимум; ал 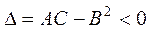 болса М(х0,у0) нүктеде экстремум жоқ;
болса М(х0,у0) нүктеде экстремум жоқ; 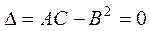 болса М(х0,у0) нүктеде экстремумның бар жоқтығы белгісіз. Екі айнымалы функцияны экстремумға мынадай ретпен зерттеген жөн: 1. Функцияның
болса М(х0,у0) нүктеде экстремумның бар жоқтығы белгісіз. Екі айнымалы функцияны экстремумға мынадай ретпен зерттеген жөн: 1. Функцияның  және
және 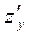 дербес туындыларын табу; 2.
дербес туындыларын табу; 2.  теңдеулер жүйесін шешіп, күдікті нүктелерді табу; 3. Функцияның екінші ретті дербес туындыларын тауып, экстремумның жеткілікті шарты бойынша экстремумның бар жоқтығын анықтау; 4. Функция экстремумдарын (экстремум нүктедегі) мәнін табу. ШАРТТЫ ЭКСТРЕМУМ. ЛАГРАНЖ ӘДІСІ Екі айнымалы функция экстремумын оның бүкіл анықталу облысында емес, тек берілген шартты қанағаттандыратын жиында қарастырайық. Айталық z= f(x, y) функциясының х және у аргументтері байланыс теңдеуі деп аталатын g(x,y) = 0 теңдеуін қанағатандырсын. А-ма. М(х0,у0) нүктенің жақын маңайында жатқан g(x,y) = 0 теңдеуін қанағатандыратын барлық (х, у) нүктелер үшін f(х0,у0)
теңдеулер жүйесін шешіп, күдікті нүктелерді табу; 3. Функцияның екінші ретті дербес туындыларын тауып, экстремумның жеткілікті шарты бойынша экстремумның бар жоқтығын анықтау; 4. Функция экстремумдарын (экстремум нүктедегі) мәнін табу. ШАРТТЫ ЭКСТРЕМУМ. ЛАГРАНЖ ӘДІСІ Екі айнымалы функция экстремумын оның бүкіл анықталу облысында емес, тек берілген шартты қанағаттандыратын жиында қарастырайық. Айталық z= f(x, y) функциясының х және у аргументтері байланыс теңдеуі деп аталатын g(x,y) = 0 теңдеуін қанағатандырсын. А-ма. М(х0,у0) нүктенің жақын маңайында жатқан g(x,y) = 0 теңдеуін қанағатандыратын барлық (х, у) нүктелер үшін f(х0,у0) 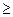 f(x,y) теңсіздігі орындалса, М(х0,у0) функцияның шартты максимум нүктесі деп, ал f(х0,у0)
f(x,y) теңсіздігі орындалса, М(х0,у0) функцияның шартты максимум нүктесі деп, ал f(х0,у0) 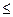 f(x,y) теңсіздігі орындалса, М(х0,у0) функцияның шартты минимум нүктесі деп аталады. Функцияныңшартты экстремумын қарапайым жағдайларда бір айнымалы функция экстремумын табуға келтіреді.. Мынадай теорема дұрыс болады. Теорема. Егер (х0,у0) нүкте z= f(x, y) функциясының g(x,y) = 0шартын қанағаттандыратын шартты экстремум нүктесі болса, онда қандай да бір
f(x,y) теңсіздігі орындалса, М(х0,у0) функцияның шартты минимум нүктесі деп аталады. Функцияныңшартты экстремумын қарапайым жағдайларда бір айнымалы функция экстремумын табуға келтіреді.. Мынадай теорема дұрыс болады. Теорема. Егер (х0,у0) нүкте z= f(x, y) функциясының g(x,y) = 0шартын қанағаттандыратын шартты экстремум нүктесі болса, онда қандай да бір  табылады да,
табылады да,  нүкте L(x, y,
нүкте L(x, y,  ) функциясының экстремум нүктесі болады. Сонымен, z= f(x, y) функциясының g(x,y) = 0 шартын қанағаттандыратын шартты экстремумын табу үшін мынадай жүйені шешу керек:
) функциясының экстремум нүктесі болады. Сонымен, z= f(x, y) функциясының g(x,y) = 0 шартын қанағаттандыратын шартты экстремумын табу үшін мынадай жүйені шешу керек:  Бұл жүйедегі соңғы теңдеу - байланыс теңдеуі. Ал бастапқы екі теңдеуді мынадай түрде жазуға болады: grad f = -
Бұл жүйедегі соңғы теңдеу - байланыс теңдеуі. Ал бастапқы екі теңдеуді мынадай түрде жазуға болады: grad f = -  grad g, яғни, шартты экстремум нүктесінде f(x, y) және g(x,y) функцияларының градиенттері коллинеар болады..
grad g, яғни, шартты экстремум нүктесінде f(x, y) және g(x,y) функцияларының градиенттері коллинеар болады..
41. Дифференциалдық теңдеулер. Коши есебі
.Анықтама. Дифференциалды теңдеу деп х тәуелсіз айнымалы, у(х) ізделінді функция және оның түрлі ретті туындыларын өз ара байланыстыратын теңдеуді айтамыз. 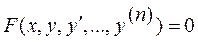 Дифференциалды теңдеу ретi деп теңдеудегі туындының жоғары ретін айтамыз.Мысалы, xy'+y=0,
Дифференциалды теңдеу ретi деп теңдеудегі туындының жоғары ретін айтамыз.Мысалы, xy'+y=0,  - бірінші ретті дифференциалды теңдеулер;
- бірінші ретті дифференциалды теңдеулер;  - екінші ретті дифференциалды теңдеу;
- екінші ретті дифференциалды теңдеу;  - үшінші ретті дифференциалды теңдеу. Бірінші ретті дифференциалды теңдеуді қарастырайық,
- үшінші ретті дифференциалды теңдеу. Бірінші ретті дифференциалды теңдеуді қарастырайық,  . Егер осы теңдеу функция туындысына қатысты шешіліп тұрса
. Егер осы теңдеу функция туындысына қатысты шешіліп тұрса 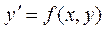 деп жазылады. Дифференциалды теңдеудегі орнына қойғанда оны тепе-теңдікке айналдыратын, дифференциалданатын y=q(x,С) функциясын теңдеудің жалпы шешімі деп айтамыз. Мысалы, xy'+y=0 теңдеудің жалпы шешімі
деп жазылады. Дифференциалды теңдеудегі орнына қойғанда оны тепе-теңдікке айналдыратын, дифференциалданатын y=q(x,С) функциясын теңдеудің жалпы шешімі деп айтамыз. Мысалы, xy'+y=0 теңдеудің жалпы шешімі 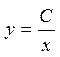 болады. Шынында да, осы функция теңдеуді тепе-теңдікке айналдырады,
болады. Шынында да, осы функция теңдеуді тепе-теңдікке айналдырады, 

 .Дифференциалды теңдеудің жалпы шешімінен қандай да бір нақты С=С0 мәнінде алынатын шешім теңдеудің дербес шешімі деп аталады. Анықтама.
.Дифференциалды теңдеудің жалпы шешімінен қандай да бір нақты С=С0 мәнінде алынатын шешім теңдеудің дербес шешімі деп аталады. Анықтама. 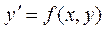 теңдеудің берілген бастапқы у(х0)=у0 шартты қанағаттандыратын шешімін табуды Коши есебі дейді. Дифференциалды теңдеудің шешімін табу процесін теңдеуді интегралдау дейді.
теңдеудің берілген бастапқы у(х0)=у0 шартты қанағаттандыратын шешімін табуды Коши есебі дейді. Дифференциалды теңдеудің шешімін табу процесін теңдеуді интегралдау дейді.
42. Айнымалылары ажыратылатын дифференциалдық теңдеулер. Мысалдар.
Егер (2) теңдеу мынадай түрде  жазылатын болса, ол айнымалысы ажыратылатын дифференциалды теңдеу деп аталады. Бұл теңдеуді шешу үшін теңдеудің екі жағын
жазылатын болса, ол айнымалысы ажыратылатын дифференциалды теңдеу деп аталады. Бұл теңдеуді шешу үшін теңдеудің екі жағын  көбейткішке бөлеміз:
көбейткішке бөлеміз:  Сонда dx алдында тек х -тен тәуелді, ал dy алдында тек у -тен тәуелді функция тұрады да, теңдеудің айнымалылары ажыратылады. Енді теңдеуді мүшелеп интегралдап шешімін табуға болады:
Сонда dx алдында тек х -тен тәуелді, ал dy алдында тек у -тен тәуелді функция тұрады да, теңдеудің айнымалылары ажыратылады. Енді теңдеуді мүшелеп интегралдап шешімін табуға болады: 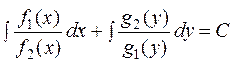 . Мысалы, xy'+y=0 дифференциалды теңдеудің шешімін табайық.
. Мысалы, xy'+y=0 дифференциалды теңдеудің шешімін табайық.  екенін ескеріп теңдеуді мына түрде жазайық
екенін ескеріп теңдеуді мына түрде жазайық  Теңдеудің екі жағын ху көбейткішке бөліп айнымалысын ажыратамыз:
Теңдеудің екі жағын ху көбейткішке бөліп айнымалысын ажыратамыз:  . Мүшелеп интегралдасақ, lny+lnx=lnC, осыдан
. Мүшелеп интегралдасақ, lny+lnx=lnC, осыдан 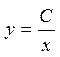 екендігі шығады.
екендігі шығады.
43. Бірінші ретті біртекті сызықты дифференциалдық теңдеулер. Мысалдар
. Егер теңдеу (2’) мынадай түрде y' =  жазылатын болса, ол бiртектi дифференциалды теңдеу деп аталады.Бұл теңдеуді шешу үшін
жазылатын болса, ол бiртектi дифференциалды теңдеу деп аталады.Бұл теңдеуді шешу үшін 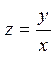 деген жаңа айнымалы енгіземіз. Осыдан
деген жаңа айнымалы енгіземіз. Осыдан 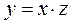 , дифференциалдап,
, дифференциалдап,  , (4) теңдеуге қоямыз:
, (4) теңдеуге қоямыз:  .
.  екенін ескеріп теңдеуді мына түрде көшіріп жазсақ:
екенін ескеріп теңдеуді мына түрде көшіріп жазсақ:  .Айнымалысы ажыратылатын теңдеу аламыз. Теңдеудің екі жағын
.Айнымалысы ажыратылатын теңдеу аламыз. Теңдеудің екі жағын  көбейткішке бөліп айнымалысын ажыратамыз,
көбейткішке бөліп айнымалысын ажыратамыз,  Біртекті дифференциалды теңдеу біртекті функция ұғымымен байланысты.
Біртекті дифференциалды теңдеу біртекті функция ұғымымен байланысты.  функциясы k ретті біртекті функция деп аталады, егер кез-келген
функциясы k ретті біртекті функция деп аталады, егер кез-келген  саны үшін мынадай теңдік орындалса:
саны үшін мынадай теңдік орындалса: 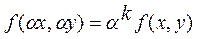 Мысалы,
Мысалы,  -екінші ретті біртекті функция, себебі
-екінші ретті біртекті функция, себебі 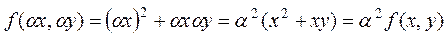 .Ал
.Ал  - нолінші ретті біртекті функция, себебі
- нолінші ретті біртекті функция, себебі 
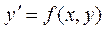 дифференциалды теңдеудегі
дифференциалды теңдеудегі  функция нолінші ретті біртекті функция болса, онда теңдеу (4) біртекті түрге келтіріледі. Мысалы,
функция нолінші ретті біртекті функция болса, онда теңдеу (4) біртекті түрге келтіріледі. Мысалы,  теңдеуді шешу керек. Шешуі.
теңдеуді шешу керек. Шешуі.  екенін ескеріп теңдеуді мына түрде жазайық:
екенін ескеріп теңдеуді мына түрде жазайық:  . Сонда
. Сонда 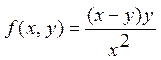 - нолінші ретті біртекті функция болғандықтан ол біртекті түрге келеді:
- нолінші ретті біртекті функция болғандықтан ол біртекті түрге келеді: 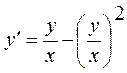 Шешу үшін
Шешу үшін 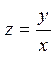 деген жаңа айнымалы енгізіп, осыдан
деген жаңа айнымалы енгізіп, осыдан 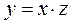 , дифференциалдап,
, дифференциалдап, 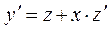 , теңдеуге қоямыз:
, теңдеуге қоямыз:  .
.  екенін ескеріп теңдеуді мына түрде көшіріп жазсақ:
екенін ескеріп теңдеуді мына түрде көшіріп жазсақ:  . Айнымалысы ажыратылатын теңдеу аламыз. Теңдеудің екі жағын
. Айнымалысы ажыратылатын теңдеу аламыз. Теңдеудің екі жағын  көбейткішке бөліп айнымалысын ажыратамыз,
көбейткішке бөліп айнымалысын ажыратамыз, 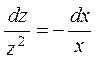 Мүшелеп интегралдасақ,
Мүшелеп интегралдасақ,  , осыдан
, осыдан  . Енді
. Енді 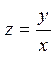 белгілеуді орнына қойсақ
белгілеуді орнына қойсақ  екендігі шығады. Алынған шешім болып тұрған функция айқын емес түрде алынды. Кейде оны дифференциалды теңдеудің жалпы интегралы деп те атайды
екендігі шығады. Алынған шешім болып тұрған функция айқын емес түрде алынды. Кейде оны дифференциалды теңдеудің жалпы интегралы деп те атайды
44. Бірінші ретті сызықты дифференциалдық теңдеулер. Мысалдар.
Бiрiншi реттi дифференциалды теңдеу сызықты деп аталады, егер ол мынадай түрде жазылатын болса: y'+P(x)y=Q(x) Егер (5) теңдеудегі Q(x)=0 болса сызықты теңдеу біртекті деп аталады y'+P(x)y=0. Сызықты біртекті дифференциалды теңдеу шешімін айнымалыны алмастыру әдісімен бірден алуға болады: 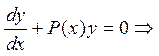

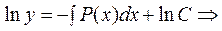

 Сонымен, сызықты бiртектi дифференциалды теңдеудiң жалпы шешiмi мынадай:
Сонымен, сызықты бiртектi дифференциалды теңдеудiң жалпы шешiмi мынадай:  .Енді (5) теңдеуді шешумен айналысайық. Лагранж әдісі: Бұл әдіс (5) теңдеу шешімін сәйкес біртекті теңдеуінің шешімінен алады. Біртекті теңдеуінің шешіміндегі С шаманы х -тен тәуелді функция деп қарастырамыз
.Енді (5) теңдеуді шешумен айналысайық. Лагранж әдісі: Бұл әдіс (5) теңдеу шешімін сәйкес біртекті теңдеуінің шешімінен алады. Біртекті теңдеуінің шешіміндегі С шаманы х -тен тәуелді функция деп қарастырамыз  С(х) функциясын табу үшін у және
С(х) функциясын табу үшін у және  мәндерін (5) теңдеуге қоямыз.
мәндерін (5) теңдеуге қоямыз.  тауып алайық:
тауып алайық: 
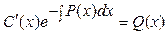 ;
; 
 екенін ескеріп, мынаны аламыз:
екенін ескеріп, мынаны аламыз:  .Мүшелеп интегралдап, белгісіз С(х) функцияны табамыз:
.Мүшелеп интегралдап, белгісіз С(х) функцияны табамыз:  С(х) функция мәнін (*) теңдеуге қойып сызықты дифференциалды теңдеу шешімін аламыз:
С(х) функция мәнін (*) теңдеуге қойып сызықты дифференциалды теңдеу шешімін аламыз: 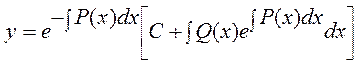 Мысал.
Мысал. 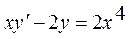 дифференциалды теңдеуді шешу керек. Шешуі. Теңдеудің екі жағын х- ке бөлсек, сызықты теңдеу аламыз:
дифференциалды теңдеуді шешу керек. Шешуі. Теңдеудің екі жағын х- ке бөлсек, сызықты теңдеу аламыз:  , мұнда P(x)=
, мұнда P(x)=  , Q(x)=2x3 . Теңдеудің шешімін табу үшін (7) формуланы қолданамыз.
, Q(x)=2x3 . Теңдеудің шешімін табу үшін (7) формуланы қолданамыз. 
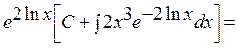


 Сонымен, берілген сызықты теңдеу шешімі:
Сонымен, берілген сызықты теңдеу шешімі: 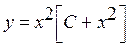 .
.
46. Ықтималдықтың классикалық және статистикалық анықтамасы
Анықтама. Сынақ нәтижесінде орындалуы да орындалмауыда мүмкін болатын оқиғаны кездейсоқ оқиға дейміз. Кездейсоқ оқиғаларды латын алфавитінің А, В, С бас әріптерімен белгілейді А-ма. Сынақ нәтижесінде міндетті түрде болатын оқиға ақиқат оқиға деп, ал сынақ нәтижесінде ешқашан орындалмайтын оқиға жалған оқиға д а. Әдетте ақиқат оқиғаны U, ал жалған оқиғаны V әріптерімен белгілеу қабылданған. А-ма. Кездейсоқ оқиғалардың бiреуiнiң пайда болуы басқасының пайда болуын жоққа шығарса олар өзара үйлесiмсiз деп аталады. Ал оқиғалардың бiреуiнiң пайда болуы басқасының пайда болуына әсер етпесе олар өзара үйлесiмдi деп аталады. Тәжірибе нәтижесінде пайда болатын барлық мүмкін оқиғалар элементар оқиғалар жиынын құрайды. Элементар оқиғалар қос-қостан үйлесімсіз болса, олар оқиғалардың толық тобын құрайды дейді. А-ма. Тәжірибедегі ізделінді оқиғаның пайда болуына қолайлы жағдайларсанының, барлық элементар оқиғалар санына қатынасы оқиға ықтималдығы деп аталады және Р әрпімен белгілейді:  мұндағы А – ізделінді оқиға, т - осы оқиғаның пайда болуына қолайлы жағдайлар саны, п - элементар оқиғалар саны. Осы анықтаманы ықтималдықтың классикалық анықтамасы деп атайды.Ы-тың классикалық анықтамасынан мынадай қасиеттер шығады:1. Ақиқат оқиға ықтималдығы бірге тең:
мұндағы А – ізделінді оқиға, т - осы оқиғаның пайда болуына қолайлы жағдайлар саны, п - элементар оқиғалар саны. Осы анықтаманы ықтималдықтың классикалық анықтамасы деп атайды.Ы-тың классикалық анықтамасынан мынадай қасиеттер шығады:1. Ақиқат оқиға ықтималдығы бірге тең:  .Шынында да, ақиқат оқиға үшін m=n. Онда
.Шынында да, ақиқат оқиға үшін m=n. Онда  . 2. Жалған оқиға ықтималдығы бірге тең:
. 2. Жалған оқиға ықтималдығы бірге тең: 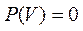 . Шынында да, ақиқат оқиға үшін m =0. Онда
. Шынында да, ақиқат оқиға үшін m =0. Онда  . 3. Кездейсоқ оқиға ықтималдығы ноль мен бірдің арасында жататын нақты сан болад
. 3. Кездейсоқ оқиға ықтималдығы ноль мен бірдің арасында жататын нақты сан болад  .Шынында да, кездейсоқ оқиға үшін 0<m<n. Теңсіздіктің екі жағын n-ге бөліпсек,
.Шынында да, кездейсоқ оқиға үшін 0<m<n. Теңсіздіктің екі жағын n-ге бөліпсек,  аламыз, олай болса:
аламыз, олай болса:  .Осы үш қасиеттен кез келген оқиға үшін мына теңсіздік орындалатыны шығады:
.Осы үш қасиеттен кез келген оқиға үшін мына теңсіздік орындалатыны шығады:  . Ы-тың классикалық анықтамасы оқиғалар саны шексіз болғанда қолданылмай қалады. Кейде оқиғалардың толық топ құратынын анықтау қиынға соғады. Сондай жағдайларда ықтималдықтың стаатистикалық анықтамасын қолданады. Тәуелсіз п рет тәжірибе жасадық дейік. Әр жолы ізделінді А оқиғаның пайда болу ықтималдығы тұрақты
. Ы-тың классикалық анықтамасы оқиғалар саны шексіз болғанда қолданылмай қалады. Кейде оқиғалардың толық топ құратынын анықтау қиынға соғады. Сондай жағдайларда ықтималдықтың стаатистикалық анықтамасын қолданады. Тәуелсіз п рет тәжірибе жасадық дейік. Әр жолы ізделінді А оқиғаның пайда болу ықтималдығы тұрақты  болсын. Тәжірибе нәтижесінде А оқиғасы т рет пайда болды дейік А-ма. Тәжірибе нәтижесінде А оқиғасы пайда болған оқиғалар санының барлық тәжірибелер санына қатынасы оқиғаның салыстырмалы жиілігі деп аталады
болсын. Тәжірибе нәтижесінде А оқиғасы т рет пайда болды дейік А-ма. Тәжірибе нәтижесінде А оқиғасы пайда болған оқиғалар санының барлық тәжірибелер санына қатынасы оқиғаның салыстырмалы жиілігі деп аталады  , мұндағы m - А оқиғасы пайда болған тәжірибелер саны, ал n - барлық тәжірибелер саны. Тәжрибелер саны артқан сайын оқиғаның салыстырмалы жиілігі қандай да бір тұрақты сан маңайына шоғырманған. Бұл заңдылық статистикалық тұрақтылық делінеді. Статистикалық тұрақтылыққа көз жеткізу үшін Ж.Бюффон және К.Пирсон деген ғалымдар теңгені көп рет лақтырып тәжірибе жасаған. Тәжірибе нәтижесі кестеде келтірілген:
, мұндағы m - А оқиғасы пайда болған тәжірибелер саны, ал n - барлық тәжірибелер саны. Тәжрибелер саны артқан сайын оқиғаның салыстырмалы жиілігі қандай да бір тұрақты сан маңайына шоғырманған. Бұл заңдылық статистикалық тұрақтылық делінеді. Статистикалық тұрақтылыққа көз жеткізу үшін Ж.Бюффон және К.Пирсон деген ғалымдар теңгені көп рет лақтырып тәжірибе жасаған. Тәжірибе нәтижесі кестеде келтірілген:
Тәжірибелер саны артқан сайын елтаңба түсу саны 0,5 санына жақындайды екен. Ал елтаңбаның түсу ықтималдығы  . Олай болса, салыстырмалы жиілік оқиға ықтималдығына жақындайды екен А-ма. Статистикалық тұрақтылық пайда болған кездегі салыстырмалы жиілік оқиға ықтималдығы деп қабылданады
. Олай болса, салыстырмалы жиілік оқиға ықтималдығына жақындайды екен А-ма. Статистикалық тұрақтылық пайда болған кездегі салыстырмалы жиілік оқиға ықтималдығы деп қабылданады  . Бұл анықтаманы ықтималдықтың статистикалық анықтамасы деп атайды.
. Бұл анықтаманы ықтималдықтың статистикалық анықтамасы деп атайды.
Поиск по сайту: