Комбинаторика элементтері

Өмірде қарапайым бір әрекеттен ғана тұратын оқиғалар аз кездеседі. Көбіне бір оқиға орындалуының әртүрлі әдістері бар болады немесе қарастыры отырған оқиғаны бірнеше кезеңдерге бөліп орындау керек болады. Осындай оқиға­лардың жалпы және қолайлы жағдайлар санын есептеуге мүмкіндік беретін қосу және көбейту ережелерін білуіміз қажет.

Қосу ережесі. Қандай да бір оқиға орындалуының бірнеше m₁, m₂,..., m_k

Түрлі тәсілдері болса сол оқиғаны орындаудың барлығы m₁+m₂+...+m_k

түрлі тәсілі бар болады.

Көбейту ережесі. k кезеңнен тұратын қандай да бір оқиғаны іске асыру керек болсын. Бірінші кезеңді орындаудың m_1, екінші кезеңді орындаудың m₂т.с.с. k кезеңді орындаудың m_kтәсілі бар болса сол оқиғаны толық іске асырудың барлығы m₁×m₂×...×m_k

түрлі тәсілі болады.

Алмастырулар. п элементтен тұратын және бір-бірінен тек орналасу ретімен ғана өзгешеленетін комбинацияларды п элементтен жасалған алмастырулар деп атайды. Элементтен жасалған алмастырулар санын Р_n деп белгілейді және алмастырулар санын есептеу үшін мынадай формула қолданады:

Р_n=n! (1)Мұндағы n!=1×2×3×...×n.

Орналастырулар. N элементтің m элементінен тұратын (m<n) және бір-бірінен құрамы немесе орналасу реті бойынша өзгешеленетін комбинациялар n элементтен m элемент бойынша жасалған орналас­тырулар  деп аталады.

n элементтен m элемент бойынша жасалған орналастыру санын деп белгілейді және оны есептеу үшін мына формула қолданылады: (2)

Терулер. N элементтің m элементі­нен тұратын (m<n) және бір-бірінен құрамы бойынша ғана өзгешеленетін комбинация­лар n элементтен m элемент бойынша жасалған теру  деп аталады.

n элементтен m элемент бойынша жасал­ған теру саны деп белгіленеді және оны табу үшін мына формула қолданылады: (3)

48. Ықтималдықтардың қосу және көбейту теоремалары.

m₁+m₂+...+m_k Көбейту ережесі m₁×m₂×...×m_k. Алмастырулар. Р_n=n! Орналастырулар Терулер. Ықтималдықтарды қосу және көбейту. А мен В оқиғаларының кемінде біреуі орындалғанда пайда болатын оқиғаны осы оқиғалардың қосындысы деп атайды және А+В деп белгілейді.А мен В оқиғалары қатар пайда болғанда орындалатын оқиғаны осы оқиғалардың көбейтіндісі деп атайды және АВ деп белгілейді.

Теорема. Үйлесімсіз екі оқиға қосындысының ықтималдығы осы оқиғалардың ықтималдықтарының қосындысына тең болады: 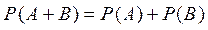. Бұл теорема оқиғалар саны екіден көп болғанда да дұрыс болады: егер А₁, А₂,..., А_n оқиғалар қос-қостан үйлесімсіз болса, онда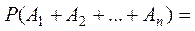 Егер А₁, А₂,..., А_n оқиғалар қос-қостан үйлесімсіз және оқиғалардың толық тобын құраса, онда . А-ма. Тәжірибе нәтижесінде мүмкін болатын екі оқиғаның бірінің пайда болуы екіншісін болдырмаса, ол оқиғалар қарама-қарсы оқиғалар деп аталады. А оқиғасына қарама-қарсы оқиғаны деп белгілейді.

Қарама қарсы оқиғалардың ықтималдықтарының қосындысы бірге тең: . А-ма. Екі оқиғаның бiреуiнiң пайда болуы екiншiсiнiң пайда болу ықтималдығын өзгертпесе олар тәуелсiз деп аталады. Ал екі оқиғаның бiреуiнiң пайда болуы екiншiсiнiң пайда болу. ықтималдығын өзгертсе, олар тәуелдi деп аталады. Теорема Тәуелсіз А мен В оқиғаларының көбейтіндісінің ықтималдығы әр оқиға ықтималдықтарының көбейтіндісіне тең: . Бұл теорема оқиғалар саны екіден көп болғанда да дұрыс болады: егер А₁, А₂,..., А_n оқиғалар қос-қостан тәуелсіз болса, онда .

49. Шартты ықтималдық. Тәуелді оқиғалар

В оқиғасының ықтималдығы А оқиғасының болған болмағанына тәуелді болатын жағдайлар болады.Сондықтан деп, шартты ықтималдық, А оқиғасы орындалып кетті деп есептегендегі В оқиғасының ықтималдығын белгілейді. Мысал. 36 картаның ішінен кез келген 2 карта алынсын. Осы екі картаның бірдей түсті болуының ықтималдығын табу керек. Шешуі. Алдымен алынған екі қартаның бірдей түске(масть) жататынын (айталық қарға) жату ықтималдығын анықтайық. Белгілеу енгізейік: А – алынған бірінші карта қарға; В – алынған екінші карта қарға. В оқиғасының ықтималдығы А оқиғасының пайда болу болмауына байланысты өзгеріп отырады. Сонымен, , . Осыдан Енді 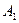, , , алынған екі карта сәйкес төрт түстің біріне жататындығын көрсететін өзара үйлесімсіз оқиғалар болсын. Сонда алынған екі картаның бірдей түсті (С оқиғасы) болуы 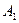, , , оқиғалардың кез келгені орындалса пайда болады, яғни,

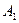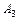С = + + + .Олай болса P(С) =P( + + + )=P()+P(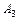)+P()+P()= Теорема. Үйлесімді екі оқиға қосындысының ықтималдығы осы оқиғалардың ықтималдықтарының қосындысынан екі оқиғаның қатар пайда болу ықтималдығын алғанға тең болады:.

51. Тәуелсіз сынақтар үшін Бернулли формуласы. Пуассон формуласы. Тәуелсіз п рет тәжірибе жасадық дейік. Әр жолы ізделінді А оқиғаның пайда болу ықтималдығы тұрақты болсын. Онда А оқиғасының пайда болмауы болады. Енді осы тәжірибелер нәтижесінде А оқиғасы k рет пайда болу ықтималдығын 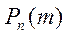деп белгілейді және ол мынаған тең: Бернулли формуласы деп атайды.Егер тәжірибелер саны көп болып (п ), ондағы А оқиғасының пайда болу ықтималдығы () аз болса, ықтималдықты Пуассон формуласымен есептеу қолайлы: 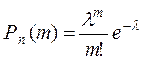мұндағы, 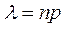, және 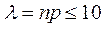деп есептейміз. Пуассон формуласын көбінесе деп жазады. Муавр-Лапластың локальді теоремасы. Тәуелсіз п рет тәжірибе жасағанда ізделінді А оқиғаның пайда болу ықтималдығы тұрақты болсын. Онда А оқиғасының k рет пайда болу ықтималдығы жуық шамамен мынаған тең: 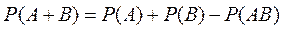, мұндағы, және п артқан сайын Муавр-Лаплас формуласының мәні дәлірек болады және бұл формуланы 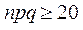болған кезде қолданған жөн. Есептеуді оңайлату үшін ықтималдықтар теориясы оқулықтарында функциясының кестесі беріледі. Бұл функция жұп, яғни f(-x)=f(x), және х артқан сайын функция нолге ұмтылады (х>4 болған кезден бастап оны нолге тең функция деп есептей беруге болады). Муавр-Лапластың интегралдық теоремасы. Тәуелсіз п рет тәжірибе жасағанда ізделінді А оқиғаның пайда болу ықтималдығы тұрақты болсын. Онда А оқиғасының пайда болу саны мен арасында болу ықтималдығы жуық шамамен мынаған тең: , мұндағы, және 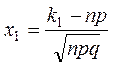, п артқан сайын Муавр-Лаплас формуласының мәні дәлірек болады және бұл формуланы 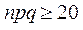болған кезде қолданған жөн. Есептеуді оңайлату үшін ықтималдықтар теориясы оқулықтарында функциясының кестесі беріледі. Бұл функция тақ, яғни f(-x)=-f(x), және х артқан сайын функция бірге ұмтылады (х>4 болған кезден бастап оны 1 тең функция деп есептей беруге болады.

52. Кездейсоқ шама. Дискретті кездейсоқ шаманың үлестірім заңдылығы. А-ма. Тәжiрибе нәтижесiнде алдын-ала белгiсiз, бiрақ нақтылы бiр мән ғана қабылдайтын шаманы кездейсоқ шама деймiз. А-ма. Ақырлы немесе ақырсыз саналатын мәндер қабылдайтын кездейсоқ шаманы дискреттi кездейсоқ шама деп атайды. А-ма. Ақырлы немесе ақырсыз аралықтағы кез келген мәндi қабылдай алатын кездейсоқ шаманы үзiлiссiз кездейсоқ шама деп атайды. КЕЗДЕЙСОҚ ШАМАНЫҢ ҮЛЕСТIРIМ ЗАҢЫ Мысал қарастырайық. Ойын сүйегiн екi рет лақтырғанда, 6 ұпай неше рет түсуi мүмкiн екенiн табайық.Жасалатын тәжiрибе: ойын сүйегiн екi рет лақтыру. Iзделiндi шама: осы екi ретте 6 ұпайдың түсу саны. Ойын сүйегiн екi рет лақтырғанда бiрде-бiр рет 6 ұпай түспеуi мүмкiн, немесе бiр рет не тiптi екi ретте де 6 ұпай түсуi мүмкiн. Сонымен, iзделiндi шаманы” қабылдайтын мүмкiн мәндерi: 0, 1, 2. Тәжiрибе алдында iзделiндi шама өзiнiң мүмкiн 3 мәнiнiң қайсысын қабылдайтыны белгiсiз, тек мiндеттi түрде осы үш мәннiң бiреуiне тең болады, яғни бұл шама - дискреттi кездейсоқ шама болады. Оны Х деп белгiлейiк:Х: х₁=0, х₂=1, x₃=2. Кездейсоқ шаманың мүмкiн мәндерiн көрсетiп қойғаннан кейiн, мынадай сұрақ туындайды: кездейсоқ шаманың осы мәндердi қабылдау мүмкiндiгi бiрдей ме, әлде әр түрлi ме? Ойын сүйегiн екi рет лақтырғанда 6 ұпайдың түспеуi түсуiне қарағанда мүмкiндiгi жоғары. Олай болса, кездейсоқ шаманың мүмкiн мәндерiмен қатар олардың осы мәндердi қабылдау мүмкiндiктерiн де көрсетiп қойсақ кездейсоқ шама жөнiндегi ұғымымыз толығырақ болар едi. Ойын сүйегiн екi рет лақтырғанда 6 ұпайдың бiрде-бiр рет түспеуi кездейсоқ оқиға, сол сияқты 6 ұпайдың бiр рет қана түсуi және екi ретте де түсуi кездейсоқ оқиғалар болады. Осы үш оқиғаны А, В, С деп белгiлейiк:А={6 ұпайдың бiрде-бiр рет түспеуi} немесе А={Х=0};В={6 ұпайдың бiр рет түсуi} немесе В={Х=1};С={6 ұпайдың екi рет түсуi}немесе С={Х=2}.Кездейсоқ оқиғалар болса, олардың ықтималдықтарын табуға болады. А оқиғасының ықтималдығын табайық. Бiрiншi рет 6 ұпай түспеуiнiң ықтималдығы , екiншi ретте де 6 ұпай түспеудiң ықтималдығы . Олай болса, .Ендi В оқиғасының ықтималдығы. Бiрiншi рет 6 ұпай түссе, екiншi рет түспеуi керек немесе бiрiншi рет алты ұпай түспесе, екiншi рет түсуi керек. Олай болса, .Ендi С оқиғасының ықтималдығы. Бiрiншi рет 6 ұпай түсуiнiң ықтималдығы 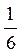, екiншi ретте де 6 ұпай түсуiнiң ықтималдығы 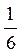. Олай болса, .Сонымен, Х-кездейсоқ шамасының х₁=0 мәнiн қабылдау ықтималдығы , х₂=1 мәнiн қабылдау ықтималдығы және x₃=2 деген мән қабылдау ықтималдығы .Сонымен кездейсоқ шаманың мәндер қабылдау мүмкiндiгiн олардың ықтималдықтарымен сипаттауға болады екен. А-ма. Кездейсоқ шаманың қабылдайтын мәндерi мен олардың сәйкес ықтималдықтарын көрсетiп жазуды дискреттi кездейсоқ шаманың үлестiрiм заңы деп атайды. Дискреттi кездейсоқ шаманың үлестiрiм заңы кездейсоқ шаманы толық сипаттайды. Бұл заңды кесте түрiнде жазып не графиктiк түрде салып көрсетедi. Кесте түрiнде жазып көрсеткенде бiрiншi жолға кездейсоқ шаманың қабылдайтын мүмкiн мәндерi жазылады да, екiншi жолда кездейсоқ шаманың сол мәндердi қабылдау ықтималдығы жазылады. Х кездейсоқ шаманың х₁ мәндi қабылдау ықтималдығын р₁, х₂ мәндi қабылдау ықтималдығын р₂, т.с.с., х_п мәндi қабылдау ықтималдығын р_п деп белгiлесек кесте мына түрде жазылàды: Осы кесте кездейсоқ шаманың үлестiрiм кестесi болады. Анықтаманы пайдаланып мысалдағы кездейсоқ шаманың үлестiрiм заңын жазайық: А, В, С оқиғаларының бiреуiнiң орындалуы басқасын болдырмайды, яғни олар үйлесiмсiз. Және де тәжiрибе нәтижесiнде осы үш оқиғадан басқа мүмкiн оқиға жоқ, онда бұлар оқиғалардың толық тобын құрайды, және ықтималдығының қосындысы бiрге тең болатыны белгiлi. Сонда осы үш оқиғаның ықтималдықтарының қосындысы бiрге тең болуы керек қой Жалпы айтсақ, кездейсоқ шаманың мүмкiн мәндерiн қабылдау ықтималдықтарының қосындысы бiрге тең болады р₁ + р₂+...+ р_п=1.

53. Дискретті кездейсоқ шаманың сандық сипаттамалары. Кездейсоқ шама өзiнiң үлестiрiм заңымен толық сипатталады. Бiрақ күнделiктi өмiрде кездейсоқ шаманың барлық мүмкiн мәндерi мен сәйкес ықтималдықтарын толық бiлу мiндеттi емес. Кездейсоқ шама жөнiнде бiлгiмiз келген кейбiр деректердi оның басқа да сипаттамаларына қарап анықтай алады екенбiз. Мұндай сипаттамаларға кездейсоқ шаманың математикалық үмiтi, дисперсиясы, орта квадраттық ауытқуы және т.б. сандық сипаттамалары жатады. 1. Кездейсоқ шаманың математикалық үмiтi. Мерген нысананы көздеп атқанда, мынадай ұпайларға алды: 6, 7, 8, 9, 10. Мергеннiң орташа ұпайы х_орт= 8. Жеткiлiктi деп санауға болатын атулардан кейiн осы ұпайларды алудың ықтималдығы есептелiп, үлестiрiм заңы жазылды Әр ұпайды алудың ықтималдығы белгiлi болғаннан кейiн мергеннiң орташа ұпайы басқаша болатынын аңғару қиын емес. Мынадай анықтама енгiзейiк. А-ма. Кездейсоқ шаманың барлық мүмкiн мәндерiн сәйкес ықтималдықтарына көбейтiп қосқаннан шыққан санды кездейсоқ шаманың математикалық үмiтi деп атайды да, М(Х) деп белгiлейдi. Математикалық үмiт кездейсоқ шаманың қабылдайтын мәндерi қандай сан маңайында шоғырланғанын көрсетедi. Математикалық үмiттi “орта шама” немесе “үлестiрiм центрi” деп те айтады. Кездейсоқ шаманың үлестiрiм заңы кесте түрiнде берiлсе, онда М(Х) мынаған тең болады:М(Х) = х₁р₁+х₂р₂+...+х_np_n. Ендi қарастырған мысалдағы мерген ұпайларының математикалық үмiтiн есептеп көрейiк. М(Х) = 10×0,01+9×0,1+8×0,15+7×0,25+6×0,49= 6,89 Сонда мергеннiң ұпайлары Х_орт=8 орта мәннiң маңайында емес, М(Х)= 6,89 математикалық үмiт маңайында шоғырланған. Математикалық үмiттiң мынадай қасиеттерi бар: 1-қасиет. Тұрақты шаманың математикалық үмiтi сол шаманың өзiне тең М(С) = С. 2-қасиет. Тұрақты шаманы математикалық үмiт таңбасы алдына шығаруға болады М(С×Х) = С×М(Х). 3-қасиет. Екi кездейсоқ шама қосындысының математикалық үмiтi олардың математикалық үмiттерiнiң қосындысына тең М(Х+У) = М(Х)+М(У) 4-қасиет. Тәуелсiз екi кездейсоқ шама көбейтiндiсiнiң математикалық үмiтi олардың математикалық үмiттерiнiң көбейтiндiсiне тең М(Х×У) = М(Х)×М(У). Кездейсоқ шаманың математикалық үмiттен ауытқуын табуға болады. Мысалда қарастырған мерген ұпайларының М(Х) = 6,89 математикалық үмiттен ауытқуын табайық. Ол үшiн мынадай екi кездейсоқ шамалар қосындысының үлестiрiм заңын табу жеткiлiктiСонда Х-М(Х) ауытқудың үлестiрiм заңы мынадай боладыЕндi осы Х-6,89 кездейсоқ шаманың математикалық үмiтiн табайық М(Х-6,89)=3,11×0,01+2,11×0,1+1,11×0,15+0,11×0,25-0,89×0,49=0 5-қасиет. Кездейсоқ шаманың математикалық үмiттен ауытқуының математикалық үмiтi нөлге тең М(Х-М(Х))=0. Осы қасиеттердiң қолданысын көрсететiн мысал қарастырайық. Тәуелсiз Х және У кездейсоқ шамаларының математикалық үмiттерi сәйкес 7-ге және 9-ға тең. а) 3Х, б) Х+У, в) Х×У кездейсоқ шамаларының математикалық үмiтiн табайық. Шешуі. М(Х)=7, M(У)=9. а) 3Х кездейсоқ шаманың математикалық үмiтiн табу үшiн 2-қасиеттi қолданамыз. Мұндағы тұрақты сан 3, олай болса М(3Х) =3×М(Х) =3×7=21. б) Х+У кездейсоқ шаманың математикалық үмiтiн табу үшiн 3-қасиеттi қолданамыз. Сонда М(Х+У) = М(Х)+М(У)=7+9=16. в) Х×У кездейсоқ шаманың математикалық үмiтiн табу үшiн 4-қасиеттi қолданамыз. Сонда М(Х×У) = М(Х) ×М(У)=7×9=63. Кездейсоқ шаманың дисперсиясы мен орта квадраттық ауытқуы Екi мергеннiңцентрден ауытқуларының үлестiрiм заңдары белгiлiОсы екi мергеннiң бiреуiн ғана жоғары деңгейдегi жарысқа таңдап алу керек. Ол үшiн екi кездейсоқ шама математикалық үмiттерiн салыстырып қайсысы аз мәнге ие болса соны таңдап аламыз (себебi, центрден аз ауытқыған). Математикалық үмiттерiн есептейiк М(Х)=1×0,4+2×0,3+3×0,2+4×0,1=2; M(У)=0×0,1+1×0,45+3×0,35+5×0,1=2. Екi кездейсоқ шаманың да математикалық үмiттерi бiрдей болып қалды М(Х)=М(У), яғни екi мерген көрсеткiштерi ауытқуларының орта шамасы бiрдей. Кездейсоқ шамалардың математикалық үмiттен ауытқуының математикалық үмiтiн алу да бiзге ешқандай нәтиже бермейдi, себебi 5-қасиет бойынша ол әруақытта нөлге тең. Мынадай жаңа ұғым енгiзейiк. А-ма. Кездейсоқ шаманың математикалық үмiттен ауытқуы квадратының математикалық үмiтiн дисперсия деп атайды да, D(X) деп белгiлейдi: D(Х)=М[{Х-М(Х)}²]. Әдетте дисперсия оңай есептелiнетiн мынадай теорема қолданылады. Т-ма. Х кездейсоқ шаманың дисперсиясы Х² кездейсоқ шаманың математикалық үмiтi мен Х кездейсоқ шаманың математикалық үмiтi квадратының айырымына тең D(Х)=М(Х²)-[М(Х)]². Дисперсия кездейсоқ шама мәндерiнiң математикалық үмiттен қаншалықты шашырап орналасқандығын көрсетедi. Мысалдағы екi мергеннiң де дисперсияларын есептейiк. Ол үшiн Х² және У² кездейсоқ шамалардың үлестiрiм заңын жазып алайықМ(Х²) пен М(У²) есептейiк М(Х²)=1×0,4+4×0,3+9×0,2+16×0,1=5; M(У²)=0×0,1+1×0,45+9×0,35+25×0,1=6 Ендi дисперсияларын есептейiк D(X)=М(Х²)-[М(Х)]²=5-2=3; D(У)=М(У²)-[М(У)]²=6,1-2=4,1. Екi кездейсоқ шаманың дисперсиялары әртүрлi: D(X)=3 және D(У)=4,1. Бiрiншi мергеннiң көрсеткiштерi екiншi мерген көрсеткiштерiне қарағанда орта шамадан шашырауы аз. Басқаша айтсақ бiрiншi мергеннiң көрсеткiштерi орта шама маңайында, екiншiге қарағанда, көбiрек шоғырланған. Бұл қортынды жоғары деңгейдегi жарысқа бiрiншi мергеннiң таңдалуына негiз болады.Дисперсияның бiрнеше қасиеттерiн келтiрейiк. 1-қасиет. Тұрақты шаманың дисперсиясы нөлге тең D(С) = 0. 2-қасиет. Тұрақты шаманы дисперсия таңбасы алдына квадраттап алып шығаруға болады D(С×Х) = С²×М(Х). 3-қасиет. Екi кездейсоқ шама қосындысының дисперсиясы олардың дисперсияларының қосындысына тең D(Х+У) = D(Х)+D(У). 4-қасиет. Екi кездейсоқ шама айырымының дисперсиясы олардың дисперсияларының қосындысына тең D(Х-У) = D(Х)+D(У). Осы қасиеттердiң қолданысын көрсететiн мысал қарастырайық. Тәуелсiз Х және У кездейсоқ шамаларының дисперсиялары сәйкес 8-ге және 10-ға тең. а) 3Х, б) Х+У, в) Х-У кездейсоқ шамаларының дисперсияларын табабу керек. Шешуі. D(Х)=8, D(У)=10. а) 3Х кездейсоқ шаманың дисперсияларын табу үшiн 2-қасиеттi қолданамыз. Мұндағы тұрақты сан 3, олай болса D(3Х) =3²×D(Х) =9×8=72. б) Х+У кездейсоқ шаманың дисперсияларын табу үшiн 3-қасиеттi қолданамыз. Сонда D(Х+У) = D(Х)+D(У)=8+10=18. в) Х-У кездейсоқ шаманың дисперсияларын табу үшiн 4-қасиеттi қолданамыз. Сонда D(Х-У) = М(Х)+М(У)= 8+10=18. Орта квадраттық ауытқу. Кездейсоқ шаманың, математикалық үмiтi сызықты өлшемдi, ал дисперсиясы квадрат өлшемдi. Мысалы егер кездейсоқ шама метрмен өлшенсе, оның математикалық үмiтi де метрмен өлшенедi, ал дисперсиясы кв.метрмен өлшенедi. Осы айырмашылықты жою үшiн мынадай жаңа ұғым енгiземiз. А-ма. Кездейсоқ шама дисперсиясынан алынған квадрат түбiр орта квадраттық ауытқу деп аталады да деп белгiленедi: . Орта квадраттық ауытқу дисперсияның квадрат түбiрi болғандықтан, оның өлшемi сызықты болады, яғни кездейсоқ шама өлшемiмен бiрдей. Орта квадраттық ауытқу да кездейсоқ шама қабылдайтын мәндерiнiң математикалық үмiттен қаншалықты шашыраңқы орналасқанын көрсетедi. Жоғарыда қарастырылған мергендердiң центрден ауытқуларының орта квадраттық ауытқуын табайық. D(X)=3 және D(У)=4,1, олай болса , .

54. Үзіліссіз кездейсоқ шама. Ықтималдықтардың үлестірім заңдылығы және негізгі сандық сипаттамалар.

Х кездейсоқ шама дискретті болса оның үлестірім заңы кесте түрінде жазылады. Ал үзіліссіз кездейсоқ шаманың қабылдайтын мәндері шексіз болғандықтан ондай үлестірім заң жазылмайды. Сондықтан үлестірім функциясы ұғымын енгіземіз. А-ма. Х кездейсоқ шаманың х нақты саннан кіші мән қабылдау ықтималдығын кездейсоқ шаманың үлестірім функциясы деп атайды және Ғ(х) деп белгілейді: F(х) = Р (Х < x). Кейде үлестірім функциясын «интегралдық функция» деп те атайды.Үлестірім функциясының қасиеттері: 1-қасиет. (анықтама бойынша үлестірім функциясы ықтималдық болып табылады). 2-қасиет. 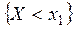Үлестірім функциясы кемімейтін функция, яғни болса ( оқиғасы оқиғасын қамтиды). 3-қасиет. ( оқиғасы жалған оқиға болғандықтан , оқиғасы ақиқат оқиға болғандықтан ). 4-қасиет. . А-ма. Кездейсоқ шаманың үлестірім функциясынан алынған туынды кездейсоқ шаманың үлестірім тығыздығы деп аталады және f(x) деп белгіленеді: Кейде үлестірім тығыздығын «дифференциалдық функция» деп те атайды. Дифференциалдық функция Х кездейсоқ шаманың мәндері тәжірибені қайталап жасағанда х нақты санының маңайында қаншалықты жиі пайда болатындығын көрсетеді.Дифференциалдық функция белгілі болғанда кездейсоқ шаманың үлестірім функциясын табу қиын емес: .Дифференциалдық функция қасиеттері: 1-қасиет. 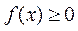(кемімейтін функция туындысы теріс болмайды). 2-қасиет. 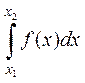,себебі, .

3-қасиет. . Мысал. Х кездейсоқ шама үлестірім тығыздығымен берілген 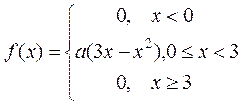.Табу керек: 1) белгісіз а -ны; 2) ; 3) Интегралдық функцияны; 4) Дифференциалдық және интегралдық функция графиктерін салу. Шешуі. 1) Дифференциалдық функцияның қасиеті бойынша . Біздің жағдайымызда тығыздық үш интервалда және әр интервалда тығыздық түрлі формулалармен берілген, сондықтан: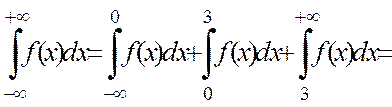

. Сонда, осыдан 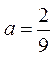. . 3) Интегралдық функцияны табайық. .4) Дифференциалдық және интегралдық функция графиктері суретте көрсетілген.

ҮЗІЛІССІЗ КЕЗДЕЙСОҚ ШАМАНЫҢ САНДЫҚ СИПАТТАМАЛАРЫ А-ма. Үзіліссіз кездейсоқ шаманың математикалық үміті деп оның х мәні мен үлестірім тығыздығы көбейтіндісінен алынған анықталған интегралы айтады . Мұндағы меншіксіз интегралды жинақталады деп қарастырамыз (егер жинақталмаса кездейсоқ шаманың математикалық үміті жоқ болады). Егер үзіліссіз кездейсоқ шаманың М(х) математикалық үміті бар болып, оның f(x) үлестірім тығыздығы жұп функция болса, онда М(х) = 0 болады. Жалпы, егер кездейсоқ шаманың f(x) үлестірім тығыздығы қандай да бір х=а нүктесіне қарағанда симметриялы болса, онда М(х) = а болады. А-ма. Үзіліссіз кездейсоқ шаманың дисперсиясы деп оның х мәнінің математикалық үміттен ауытқуының квадраты мен үлестірім тығыздығы көбейтіндісінен алынған анықталған интегралы айтады . Әдетте дисперсия оңай есептелiнетiн мынадай формула қолданылады:

Үзіліссіз кездейсоқ шама дисперсиясынан алынған квадрат түбiр орта квадраттық ауытқу болады: .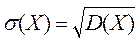

55. Биномдық және Пуассон үлестірімі

Егер Х кездейсоқ шаманың қабылдайтын мүмкін мәндері болып, ал осы мәндерді қабылдау ықтималдығы Бернулли формуласымен анықталса онда кездейсоқ шама биномдық үлестірім заңымен берілген деп аталады

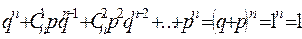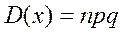орындалған. Шынымен бұл қосынды Ньютон биномы бойынша: Теорема. Биномдық үлестірім заңымен берілген X кездейсоқ шамасының математикалық күтімі , ал дисперсиясы тең 2. Пуассон үлестірімі. Егер Х кездейсоқ шаманың қабылдайтын мүмкін мәндері болып, ал осы мәндерді қабылдау ықтималдығы Пуассон формуласымен анықталса онда кездейсоқ шама Пуассон үлестірім заңымен берілген д.а

орындалған. Шынымен: Теорема. Пуассон үлестірім заңымен берілген кездейсоқ шаманың математикалық үміті мен дисперсиясы мынаған тең 4. Көрсеткішті (экспоненциалды) үлестірім. Егер кездейсоқ шаманың үлестірім тығыздығы 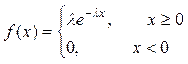арқылы берілсе, онда ол көрсеткіштік үлестірім заңымен берілген деп аталады. Үлестірім тығыздығы графигі 3-суреттегідей болады:

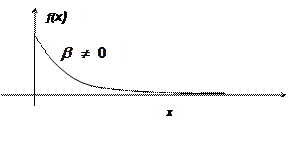
Теорема. Көрсеткішті үлестірілген кездейсоқ шааның үлестірім функциясы Үлестірім функциясы графигі 4-суретте берілген. Көрсеткіштік үлестірім заңымен берілген кездейсоқ шаманың математикалық үміті мен дисперсиясы мынаған тең:

56. Бірқалыпты үлестіру

Бірқалыпты үлестірім. Үзіліссіз кездейсоқ шаманың үлестірім тығыздығы аралығында тұрақты болып, одан тыс жерде 0-ге тең болса, онда кездейсоқ шама бірқалыпты үлестірілген деп аталады: . Бірқалыпты үлестірілген кездейсоқ шаманың үлестірім қисығы (тығыздығы) 1-суреттегідей болады.

		F(x)
	f(x)

Теорема. Бірқалыпты үлестірілген кездейсоқ шаманың үлестірім функциясы

Бірқалыпты үлестірілген кездейсоқ шаманың үлестірім функциясы 2-суреттегідей болады. Математикалық үмітін есептейі Сонымен, бірқалыпты үлестірілген кездейсоқ шаманың математикалық үміті мынаған тең екен: .

Дисперсиясы мынаған тең: Дәлелдеуі қиын емес.

 

 

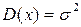57. Қалыпты үлестіру. Егер кездейсоқ шаманың үлестірім тығыздығы арқылы берілсе, онда ол қалыпты үлестірім заңымен берілген дейді. Мұндағы - параметрлер деп аталады.. Теорема. Қалыпты үлестірілген кездейсоқ шаманың математикалық үміті , дисперсиясы тең. Шынында да: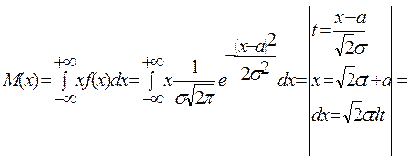

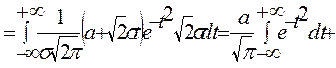
интегралы Эйлер интегралы деп аталады.

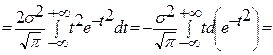
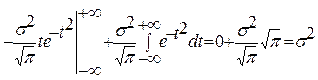
Қалыпты үлестірілген кездейсоқ шаманың үлестірім функциясы Лаплас формуласы арқылы өрнектеледі Қасиеттері: 1. Қалыпты үлестірілген кездейсоқ шаманың кесіндісіне түсу ықтималдығы мынаған тең:

мұндағы, - Лаплас функциясы.Қалыпты үлестірілген кездейсоқ шаманың 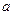математикалық үмітінен ауытқуы шамадан артпауының ықтималдығы мынағын тең: Осы формуладан ықтималдықты - ның әртүрлі мәндерінде есептейік Осыдан «үш сигма ережесі» шығады: Егер кездейсоқ шама қалыпты үлестірілген болса, онда оның математикалық үміттен ауытқуының абсолют шамасы үш орта квадраттық ауытқудан () аспайды.

 

 

59. Вариациялық қатардың сандық сипаттамалары: орта мән, дисперсия, мода, медиана, бастапқы және орталық моментттер, ассиметрия және эксцесс.

Мода және медиана. Ықтималдықтар теориясында кездейсоқ шаманың математикалық үміт, дисперсия, орташа квадраттық ауытқуынан басқа да сандық сипаттамалар қолданылады. Анықтама: Кездейсоқ шаманың ең ықтималды мәні мода деп аталады. 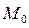белгілейді. Мысал. Дискретті кездейсоқ шаманың үлестірім заңы берілген.

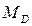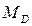Модасын табу керек. Шешуі. Кездейсоқ шаманың ықтималдықтарының ең көбі 0,5. Ол ықтималдықты Х=2 болғанда қабылдайды, ең ықтималды мән, яғни модасы . Анықтама: Егер кездейсоқ шаманың белгілі бір х = мәнінде орындалса, онда кездейсоқ шаманың медианасы деп аталады

Геометриялық тұрғыдан қарағанда х= 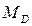түзуі үлестірім қисығы астындағы ауданды тең екіге бөледі (6-сурет Мысал. X – үзіліссіз кездейсоқ шама үлестірім тығыздығымен берілген: (7-сурет). Модасы мен медианасын табу керек.

Шешуі. Үлес тығыздығы ең үлкен мәнін болғанда қабылдайды, сондықтан . 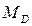= b медиананы мынадай шарттан табамыз: Сонымен, 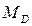= 0,79. Анықтама. X кездейсоқ шамасының - ретті бстапқы моменті деп мынадай шаманы айтады А-ма. X кездейсоқ шамасының - ретті орталық моменті деп мынадай шаманы айтады 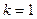болғанда бастапқы момент кездейсоқ шаманың математикалық үмітін береді , яғни кездейсоқ шаманың орта мәнін береді. болғанда орталық момент кездейсоқ шаманың дисперсиясын береді яғни кездейсоқ шаманың математикалық үміттен қаншалықты шашыраңқы орналасқанын көрсетеді. 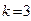болғанда орталық момент үлестірімнің ассиметриялығын сипаттайды. Кездейсоқ шаманың өлшемімен бірдей болуы үшін оны -ке ( - орташа квадраттық ауытқу) бөледі 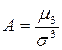Бұл шама кездейсоқ шаманың ассиметрия коэффициенті деп аталады. Егер үлестірім -ке қарағанда симметриялы болса, онда

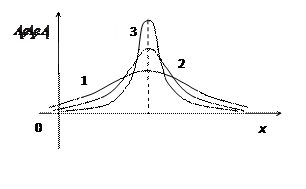
8-суретте 1 – қисық оңжақтық 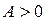ассиметрияны, ал 2 – қисық солжақтық ассиметрияны көрсетеді. болғанда орталық момент үлестірімнің сүйір не доғалданып келуін сипаттайды. Кездейсоқ шаманың эксцессі деп мынадай шаманы айтады Формулада 3 тұрған себебі, ең жиі кездесетін қалыпты үлестірімде 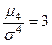. Қалыпты үлестіріммен салыстырғанда сүйірленіп келген үлестірімдердің эксцессі оң E > 0 (9-суретте 3-қисық)болады, ал қалыпты үлестіріммен салыстырғанда доғалданып келген үлестірімдердің эксцессі теріс E < 0 (9-суретте 1-қисық)болады. Қалыпты үлестірілген кездейсоқ шама ассиметрия коэффициенті мен эксцессі нолге тең болады: .

61. Сенімділік ықтималдық, сенімділік интервалы

Орта мән, дисперсия, орта квадраттық ауытқу бас жинақтың бір ғана санмен өрнектелетін бағалық параметрлері болып табылады. Бұндай бағаларды нүктелік бағалар деп атайды. Олар таңдама көлемінен тәуелді болады және нақтылы көрсеткіштен ауытқуы көп болуы мүмкін. Сондықтан бағалардың нақтылығы мен сенімділігін тексеру қажеттігі туындайды. Бұл қажеттілік интервалдық бағалар арқылы іске асады.

Қандай да бір бас жинақтың а математикалық үмітінің бағасы таңдама ортасы болып табылады:

.

Бұл баға ауытқу неғұрлым аз болса, соғұрлым дәлірек болады. Басқаша айтсақ қандай да бір саны табылып

теңсіздігін жазсақ, сонда 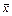таңдама ортасының бағасы аз болған жайын дәлірек дейміз. Бұл жағдайда бағаның сенімділігі деп қарастыруға болады. Таңдама құрамындағы варианталар кездейсоқтығына байланысты теңсіздігінің орындалуын қандай да бір ықтималдықпен ғана айта аламыз. Осы ықтималдықты бағаның сенімділік ықтималдығы деп атайды: немесе .

Басқаша айтсақ, интервалдың бас жинақтың а математикалық үмітін қамту ықтималдығы -ға тең.

интервал сенімділік интервалы деп аталады.

Экономикада көбінесе қалыпты үлестірілген бас жинақтың математикалық үмітін бағалау үшін жасалған сенімділік интервалы қарастырылады. Негізгі екі жағдай бар.

1-жағдай. Егер бас жинақтың орта квадраттық ауытқуы алдын ала белгілі болса, онда математикалық үмітін бағалау үшін жасалған сенімділік интервалы мынадай болады: ,

мұндағы 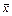- таңдама ортасы; n – таңдама көлемі; t – Лаплас функцясының 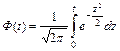кестесінен қатынасты қанағаттандыратындай етіп және алдын ала берілген сенімділік ықтималдықпен анықталады.

1 | 2 | 3 | 4 |

Поиск по сайту:

---