Ферма, Ролль, Лагранж теоремалары

Ферма теоремасы. х₀ нүктесі y=f(x) функциясының экстремум нүктесі болып ж-е осы нүктедегі f’(x₀)функция туындысы бар болса, онда f’(x)=0. Бұл теореманың геометриялық мағынасы: теорема шартын қанағаттандыратын нүктеде функция графигіне жүргізілген жанама абсцисса осіне параллель болады.

Лагранж теоремасы. Егер (x₀,y₀) нүкте z=f(x,y) функциясының g(x,y)=0 шартын қанағаттандыратын шартты экстремум нүктесі болса, онда қандай да бір λ₀ табылады да,(x₀,y₀,z₀) нүкте L (x,y,λ) функциясының экстремум нүктесі болады.

Ролль теоремасы — дифференциалдық есептеудің негізгі теоремаларының бірі. Егер f(x) функциясы axb аралығында үзіліссіз болып, осы аралықтың әрбір ішкі нүктесінде дифференциалданса және шеткі нүктелеріндегі мәндері тең болса, яғни f(a)=f(b), онда (a, b) интервалында f¢(x) функциясы нөлге айналатын кем дегенде бір с нүктесі болады: a<c<b; f¢(с)=0. Ролль теоремасын алғаш рет 1690 ж. француз математигі М.Ролль (1652 — 1719) алгебралық көпмүшеліктер үшін тұжырымдаған

28. Туындының экономикалық қолданыстары. Функция иілгіштігі

Айталық y=f(x) функциясы өндірілген өнім х көлемінен оған кеткен у шығын арасындағы байланысты сипаттасын.

Егер өндіріс көлемін х -тен -ке арттырсақ, яғни бірлікке, онда жұмсалған шығын да бірлікке көбейеді.

Ал қатынас өндіріс көлемін бірлікке өзгерткендегі орташа шығынды береді. жағдайдағы қатынастың шегі, яғни , өндірістің шектік шығынын береді.

шаманы аз деп есептесек формуланы мынадай түрде жазуға болады:

,осыдан немесе .

Егер х өте үлкен шама деп, ал шаманы аз деп, айталық деп есептесек, онда немесе 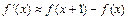. Сонымен, өндірістің шектік шығыны өндіріс көлемін бірлікке өзгерткендегі үстеме өнім өндіруге кеткен қосымша шығынға тең болады.

Мысалы, y=f(x) функциясы қандай да бір уақыт мезетінде х жұмысшының у өндірілген өнім көлемі арасындағы байланысты сипаттасын. Айталық, фирма тағы бір адамды жұмысқа қабылдады. Онда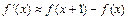

шама жаңадан келген жұмысшының өндірген өнім көлемі.

Егер С- өнім бірлігі (бағасы), ал р – фирманың жұмысшыға уақыт мезетінде төлейтін жалақысы болса, онда болған кезде фирмаға тағы бір жұмысшыны алуға болады, себебі жұмысшының фирмаға түсіретін пайдасы одан алатын жалақысынан көп. Осы ара қатынасты экономиканың алтын заңы дейді.

y=f(x) функциясы қандай да бір уақыт мезетінде у өндірілген өнім көлемінің х адам еңбегінен тәуелділігін сипаттаса, онда шаманы х нүктесіндегі шектік еңбек өнімділігі деуге болады.

Функция иілгіштігі. y=f(x) функциясы у шаманың х шамадан тәуелділігін білдірсін. Тәуелсіз аргумент шамаға өзгергенде тәуелді айнымалы да шамаға өзгереді. Мынадай сұрақ туындайды, у тәуелді айнымалының х аргумент өзгерісіне деген иілгіштігін қалай өлшеу керек. Бір айнымалының екінші айнымалыға әсерін сипаттайтын шама ретінде туындыны алуға болады. Ол функцияның аргумент өзгерісіне қатысты өзгеріс жылдамдығын сипаттайды. Бірақ экономикада бұл қолайсыздау, себебі ол шамаларды немен өлшейтінімізге байланысты. Мысалы, қандай да бір затқа деген q сұраныс функциясының оның p бағасынан тәуелділігін алсақ, онда туынды мәні (баға теңгемен өлшенгенде) сұраныс немен өлшенетіндігіне байланысты. Егер кг өлшенсе, туынды кг/тг, ал центенермен өлшенсе ц/тг болады. Баға бірдей болғанымен, туынды мәндері әртүрлі. Сондықтан экономикада бір айнымалының екінші айнымалы өзгерісіне деген сезімталдығын өрнектейтін өлшем бірліксіз шама енгізіледі. Ондай шама ретінде айнымалылардың абсолюттік өзгерістерінің қатынасы емес, олардың салыстырмалы немесе проценттік өзгерістерінің қатынасын алады, яғни

29.Функцияның экстремумның қажетті және жеткілікті шарты. х₀ нүктесінің - маңайы табылып, (х₀- х₀+ ), осы маңайдағы барлық х х₀ үшін f(x)>f(х₀) теңсіздігі орындалса, х₀ нүктесі f(x) функциясының минимум нүктесі деп, ал f(x)<f(х₀) теңсіздік орындалса, х₀ нүктесі f(x) функциясының максимум нүктесі деп аталады. Функцияның минимум және максимум нүктелерін экстремум нүктелері деп атайды. Осы нүктелердегі функция мәндерін функция экстремумдары дейді. Ферма теоремасы. х₀ нүктесі y=f(x) функциясының экстремум нүктесі болып және осы нүктедегі функция туындысы бар болса, онда =0. Экстремумның бірінші жеткілікті шарты. y=f(x) функциясы х₀ нүктесінде үзіліссіз және қандай да бір - маңайында функция туындысы бар болсын (х₀ нүктесінде туынды болмауы мүмкін). Онда,1)егер х аргумент х₀ нүкте арқылы өткенде 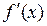таңбасын оңнан теріске өзгертсе, онда х₀ нүкте максимум нүктесі болады;2)егер х аргумент х₀ нүкте арқылы өткенде таңбасын терістен оңға өзгертсе, онда х₀ нүкте минимум нүктесі болады; 3)егер х аргумент х₀ нүкте арқылы өткенде таңбасын өзгертпесе, онда х₀ нүкте экстремум нүктесі емес. Экстремумның екінші жеткілікті шарты. y=f(x) функциясы х₀ нүктесінде үзіліссіз және қандай да бір - маңайында екі рет дифференциалдансын. Сонымен қатар болса, онда 1)егер болса, онда х₀ нүкте f(x) функциясының максимум нүктесі болады;2)егер болса, онда х₀ нүкте f(x) функциясының минимум нүктесі болады.

30. Функция графигінің дөңестегі, ойыстығы және иілу нүктелері. y=f(x) функция графигі (а,в) интервалының кез келген нүктесінде жүргізілген жанамадан төмен жатса, онда функция дөңес (дөңестігі жоғары қараған) деп, ал жанамадан жоғары жатса, онда функция ойыс (дөңестігі төмен қараған) деп аталады. атайды.Функция графигінің дөңес және ойыс бөліктерін бөліп тұратын нүктені функцияның иілу нүктесі деп атайды. Функция дөңестігінің жеткілікті шарты. (а,в) интервалында y=f(x) функциясының екінші ретті туындысы теріс таңбалы болса, функция графигі осы аралықта дөңес, ал екінші туындысы оң таңбалы болса, функция графигі осы аралықта ойыс болады. Иілу нүктесі бар болуының қажетті шарты. (а,в) интервалында екі рет дифференциалданатын y=f(x) функциясының (x₀, f(x₀)) нүктесі иілу нүктесі болса, онда

 

 

31. Асимптота. Фун-ны зерттеп, график салудың жалпы сүлбесі. Анықтама. Егер y=f(x) функциясы үшін және шектерінің ең болмағанда біреуі шексіздікке тең болса, онда функция графигінің тік асимптотасы деп аталады (6а-сурет).у=kx+b түзуі y=f(x) функция графигінің көлбеу асимптотасы деп аталады, егер функцияға тиісті қандай да бір М нүкте координат басынан алыстаған сайын түзуге шексіз жақындаса (6б-сурет).

у у М x y=f(x) х 0 а

Көлбеу асимптотаның дербес жағдайы

(k=0) горизонталь асимптота болады: y=b Көлбеу асимптотаны мынадай теорема көмегімен табуға болады. Теорема. у=kx+b түзуі y=f(x) функция графигінің көлбеу асимптотасы болуы үшін мынадай шектердің бар болуы қажетті және жеткілікті: , . Функцияны зерттеп оның графигін салуды мынадай ретпен жүргізген жөн:

1. Функцияның анықталу облысын табу;

2. функцияны жұп, тақтылыққа зерттеу;

3. функцияны периодтылыққа зерттеу;

4. функцияны үзіліссіздікке зерттеп, үзіліс нүктелерін табу;

5. күдікті нүктелерін табу;

6. монотонды аралығы мен экстремумдарын табу;

7. ойыс, дөңес аралықтарын, иілу нүктелерін табу;

8. функция графигінің асимптоталарын табу;

9. функция графигінің координаталар осімен қилысу нүктелерін;

10. зерттеулерге сүйеніп график салу.

32. Интеграл қасиеттері. Интегралдар кестесі.

. f(x) және F(x) функциялары ақырлы немесе ақырсыз Х аралықта анықталған функциялар болсын. Анықтама. Х аралығында дифференциалданатын 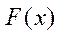функциясы теңдігін қанағаттандырса, функциясы f(х) функциясының алғашқы функциясы деп аталады Берілген функцияның алғашқы функциясын табу амалы функцияны интегралдау деп аталады. Функцияны интегралдау амалы дифференциалдау амалына кері амал. Интеграл анықтамасынан мынадай қасиеттер шығады.

1. .

2. .

3. = F(x) + C.

4. Берілген аралықта f(x) және g(x) функцияларының алғашқы функциялары бар болса, онда f(x) + g(x) функциясының да алғашқы функциясы бар болады және

5. .

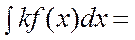
6. Егер = F(x) + C болса, онда =

F(ax+b) + C

7. Егер интеграл астындағы функцияның алымы бөлімнің туындысы болса, онда интеграл бөлімнің абсолют шамасының наткрал логарифміне тең, яғни 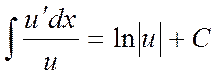, мұндағы u=u(x).

1 | 2 | 3 | 4 |

Поиск по сайту:

---