Принцип Ферма

- осн. принцип геометрической оптики, утверждающий в простейшей форме, что луч света всегда распространяется в пространстве между двумя точками по тому пути, вдоль к-рого время его прохождения меньше, чем вдоль любого из др. путей, соединяющих эти точки. Время прохождения светом расстояния l в среде с показателем преломления ппропорционально оптич. длине пути S. Для однородной среды S=nl, а для неоднородной

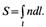Т. <о., в этой форме Ф. <п. есть принцип наименьшей оптич. длины пути. В первонач. формулировке, данной П. Ферма (P. Fermat, ок. 1660), принцип имел смысл наиболее общего закона распространения света, из к-рого следовали все (к тому времени уже известные) законы геом. оптики. Для однородной среды Ф. п. приводит к закону прямолинейности светового луча (в соответствии с положением о том, что прямая есть линия, вдоль к-рой расстояние между двумя точками наименьшее), а для случая падения луча на границу раздела между средами с разными п из Ф. <п. можно получить законы зеркальногоотражения света и преломления света.

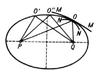
В более строгой формулировке Ф. п. представляет собой т. <н. в а р и а ц и о н н ы й п р и н ц и п, утверждающий, что реальный луч света распространяется от одной точки к другой по линии, вдоль к-рой время его прохождения э к с т р е м а л ь н о или о д и н а к о в о по сравнению с временами прохождения вдоль всех др. линий, соединяющих данные точки. Это означает, что оптич. длина пути луча может быть не только минимальной, но и максимальной либо равной всем остальным возможным путям между двумя точками. Условие экстремальности оптич. длины пути сводится к требованию, чтобы была равна нулю вариация от интеграла где А и В- точки, между к-рыми распространяется свет. Примеры мин. пути - упомянутые распространение света в однородной среде и прохождение им границы раздела двух сред с разными п. Все три случая (минимальности, максимальности и стационарности пути) можно проиллюстрировать, рассматривая отражение луча света от вогнутого зеркала (рис.). Если зеркало имеет форму эллипсоида вращения, а свет распространяется от одного его фокуса Р к другому Q (причём путь без отражения невозможен), то оптич. длина пути луча РО' + O'Q по свойствам эллипсоида равна всем остальным возмож ным, напр. РО " + O "Q; если на пути между теми же точками свет отражается от зеркала меньшей, чем у эллипсоида, кривизны (ММ), реализуется мин. путь, если же большей (зеркало NN) - максимальный.

В волновой оптике Ф. п. представляет собой предельный случай Гюйгенса - Френеля принципа и применим, если можно пренебречь дифракцией света (когда длина световой волны мала по сравнению с наименьшими характерными для задачи размерами): рассматривая лучи как нормали к волновым поверхностям, легко показать, что при всяком распространении света оптич. длины будут иметь экстремальные значения. Во всех случаях, когда необходимо учитывать дифракцию, Ф. п. (как и геом. оптика вообще) неприменим.

Поиск по сайту: