 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
РЕШЕНИЯ
1. Рассчитать прибыль можно, лишь зная затраты – в данном случае себестоимость квартиры как разность между выручкой (доходом) и затратами при каждой сделке. Скажем, если квартира обошлась в свое время Марку в 1 млн, то при первой сделке он заработал:
1,2- 1,0 = 0,2 млн у. д. ед.
При второй сделке его затраты составили также 1,0 млн (цена покупки), следовательно, здесь прибыль равна:
1,1 - 1,0 = 0,1 млн у. д. ед.
И общая прибыль составляет:
0,2 + 0,1 =0,3 млн у. д. ед.
Однако если себестоимость квартиры перед первой сделкой иная, то изменится, естественно, и прибыль.
2. Бриллиант весом в 4 карата стоит:

Это соответствует стоимости натурального рубина в х карат:

Откуда

3. 1) Литр дорогого молока продавался за 1 у. д. ед., а литр дешевого – за  у. д. ед. Литр смеси стоил:
у. д. ед. Литр смеси стоил:

а фактически продавался за  у. д. ед.
у. д. ед.
2) Таким образом, торговец на каждом литре терял:

3) Поскольку всего он потерял 50 у. д. ед., значит, было продано 50: 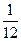 = 600 литров смеси, в которой каждого вида молока было 600: 2 = 300 литров.
= 600 литров смеси, в которой каждого вида молока было 600: 2 = 300 литров.
4) За 300 литров дорогого молока можно было выручить
300 х 1 = 300 у.д.ед.,
а за 300 литров дешевого -
300 х  = 150 у.д.ед.
= 150 у.д.ед.
Фактически за 300 литров смеси было получено
300 х  = 200 у.д.ед.
= 200 у.д.ед.
5) Следовательно, на дорогом молоке потеряно
300 – 200 = 100 у.д.ед.
а на дешевом приобретено
200- 150 = 50 у. д. ед.
4. Обозначим через х количество двухрублевых монет, а через у – пятирублевых. При этом количество однорублевых монет составит 12 х, и условие задачи можно математически выразить так:
1 х 12 x + 2 x + y = 100руб.

где х и у – целые числа (количество монет не может быть дробным числом).
Из последнего варианта следует: для того чтобы у был целым числом, разность 100 – 14х должна быть кратна 5; для этого, в свою очередь, произведение 14х должно быть кратным 5 и меньшим, чем 100.
Этим условиям удовлетворяет только 14 x = 70, 
Подставим значение x в (*), получим

Итак, количество однорублевых монет равно 12 x = 60, двухрублевых – х = 5, пятирублевых – у = 6.
5. Вопреки распространенной глазомерной оценке первый вариант, уже начиная со второго года, существенно выгоднее второго. Общая сумма выигрыша составляет 1350 у. д. ед. (около 13 %). Все дело в том, что, хотя прибавка к зарплате по второму варианту происходит в два раза чаще, чем по первому, сумма прибавки при этом значительно меньше: 50 у. д. ед. относится не к полугодовой, а к годовой зарплате. Причем, чем дальше, тем расчет по первому варианту выгоднее. Это наглядно видно из следующей таблицы:
| Первый вариант | Второй вариант |
| 1-й год 1200 у.д.ед. | 1-е полугодие 600 у. д. ед. 2-е полугодие 625 « |
| 2-й год 1400 у.д.ед. | 3-е полугодие 650 у. д. ед. 4-е полугодие 675 « |
| 3-й год 1600 у. д. ед. | 5-е полугодие 700 у. д. ед. 6-е полугодие 725 « |
| 4-й год 1 800 у. д. ед. | 7-е полугодие 750 у. д. ед. 8-е полугодие 775 « |
| 5-й год 2000 у. д. ед. | 9-е полугодие 800 у. д. ед. 10-е полугодие 825 « |
| 6-й год 2200 у. д. ед. | 11-е полугодие 850 у. д. ед. 12-е полугодие 875 « |
| Всего: 10200 у. д. ед. | Всего: 8850 у. д. ед. |
6. Обозначим сестер начальными буквами их имен: А, Б, В. Племянника Анны обозначим А1, сына Белы – Б1, мужа Веры – В1. Из условия задачи следует, что в деле участвуют шесть человек: А, Б, В, А1, Б1, В1, и прибыль в 44 млн у. д. ед. нужно разделить между ними поровну, так чтобы у каждого она выражалась целым числом миллионов у. д. ед. Поскольку это невозможно (44 не делится на 6 без остатка), напрашивается единственное допустимое решение: владельцев капитала должно быть столько, чтобы 44 млн делились между ними без остатка. Условие задачи предоставляет такую возможность. Для этого следует лишь предположить, что А1 не только племянник А, но одновременно и сын Б, и муж В. Иными словами, А1, Б1, В1 – одно и то же лицо, и прибыль следует делить между четырьмя акционерами:
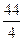 = 11 млн у. д. ед., что отвечает условию задачи.
= 11 млн у. д. ед., что отвечает условию задачи.
7. Обозначая через х и у доходы компаний А и Б пять лет назад, можно записать условие задачи следующим образом:

Решая систему из двух уравнений с двумя неизвестными, получим из (1):
х = 6у
Подставляя значение x в (2), будем иметь:
6 у + 500 - 2 y - 1000 = 0.
Откуда у = 125, х = 6у = 750.
Итак: 1) доход компании А пять лет назад был 750 тыс. у. д. ед.; доход компании Б – 125 тыс. у. д. ед.;
2) доход компании А в настоящее время 750 + 5 х 100 = 1250 тыс. у. д. ед.; доход компании Б – 125 + 5 х 100 = 625 тыс.у.д.ед.
8. Если принять долю компаньона А за единицу, то доля Б составит  , а доля В –
, а доля В –  .
.
Переходя к целым числам (для этого нужно умножить дробные доли на их общий знаменатель, равный 12), получим долю А равной 15, долю Б-10 и долю В- 18.
1) Исходя из долей, определим суммы, причитающиеся каждому компаньону:
компаньону А причитается

компаньону Б – 20 х 10 = 200 тыс. у. д. ед., компаньону В – 20 х 18 = 360 тыс. у, д. ед.
2) Из условия задачи и полученных долей ясно, что старший компаньон (В) владеет предприятием 6 лет (что в три раза меньше 18). Значит, в соответствии с долями компаньон А владеет предприятием  = 5 лет, а компаньон Б –
= 5 лет, а компаньон Б –  = 3 года и 4 месяца.
= 3 года и 4 месяца.
9. Обозначим через х сумму кредита, тогда по условиям задачи суммы выплат и остатки будут следующими:
| Выплаты | Остатки | |
| 1-й месяц кредита | 
| 
|
| 2-й месяц | 
| 
|
| 3-й месяц | 
| 
|
| 4-й месяц и т. д. | 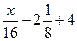
| 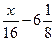
|
Помятуя, что выплаты заканчиваются в месяце, следующем за тем, в котором остаток на единицу больше, чем номер месяца, прошедшего с момента получения кредита определим, чему может быть равна сумма кредита, исходящая из этого условия.
Для остатка 1-го месяца

Для остатка 2-го месяца
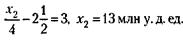
Для остатка 3-го месяца

Для остатка 4-го месяца

x1, х2, х4 (и т. д.) не подходят, потому что по условию задачи сумма кредита должна находиться в пределах 50 - 100 млн у. д. ед. Следовательно:
1) Условию задачи отвечает сумма кредита, равная х3 = 66 млн у. д. ед.
2) Кредит должен быть погашен к концу 4-го месяца.
3) Плата за кредит равна 3 % х 4 месяца, т. е. 12 % от 66 млн у. д. ед., что соответствует 7,92 млн у. д. ед.
10. 1) Обещание было дано в понедельник. 2) Деньги будут отданы в ближайшую пятницу.
11. Обозначим через х капитал игрока, у – сумму ставки на победу, z – сумму ставки на поражение. Тогда условие задачи можно записать так:

Решая совместно (1) и (2), получим:

Далее, из (1) и (2):

Подставляя полученные значения у и z в (3), будем иметь:

Итак: 1) капитал игрока был равен 200 тыс. у. д. ед.;
2) сумма ставки на победу равна 30 тыс. у. д. ед.;
3) сумма ставки на поражение равна 20 тыс. у. д. ед.
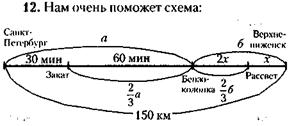
12. Обозначив расстояние от Санкт-Петербурга до бензоколонки через а, а от бензоколонки до Верхнениженска через б, сообразим в соответствии с условием задачи, что расстояние от поселка Закат до бензоколонки –  а, а от бензоколонки до поселка Рассвет
а, а от бензоколонки до поселка Рассвет  б.
б.
Следовательно, от поселка Закат до поселка Рассвет  т. е. две трети пути от Санкт-Петербурга до Верхнениженска, что составляет
т. е. две трети пути от Санкт-Петербурга до Верхнениженска, что составляет  х 150 = 100 км.
х 150 = 100 км.
Искомая плата за проезд, таким образом, равна: 100: 10= 10 у. д. ед.
13. Это возможно.
Разместив участок III так, как показано на рисунке, нетрудно убедиться, что:
III = I – а – в + а + а + б = I + а – в + б.
С другой стороны,
II = а - в + б.
Следовательно, III = I + II.

Кстати, мы только что доказали теорему Пифагора. Стороны квадратов I и II – это катеты, а стороны квадрата III – гипотенуза АБВ: сумма квадратов катетов равна квадрату гипотенузы. Просто и наглядно.
14. 1) Обозначая площадь, занимаемую оборудованием из контейнера № 1, через x, условие задачи можно математически записать так:
– площадь, занимаемая оборудованием из контейнера № 2, равна x + 10;
– площадь, занимаемая оборудованием из контейнера № 3, равна х + 20.
х+ (х+ 10) + (x + 20) = 402;
3 x + 30 = 402;
x =124м2.
Соответственно, площади, занимаемые оборудованием из контейнеров № 2 и № 3, равны 134м2 и 144м2.
2) Обозначим черз п, т и k число раз, во сколько площади цехов А, Б и В больше, чем площади оборудования из контейнеров № 1, № 2 и № 3. По условию задачи n,m и k могут иметь значения лишь 1, 1,5 и 2 каждое.
При этом должно иметь место равенство:
124 х n + 134 х m +144 х k = 613. (*)
Будем рассуждать так:
– если п = 1,5 или 2, то при любых возможных значениях т и k сумма (*) будет меньше 613; следовательно, п может быть равно только 1, а значит, контейнер № 1 предназначен для цеха Б и для значения т остается только 1,5 или 2;
– при этом если т = 2, то при любых возможных п и k сумма (*) будет меньше 613; следовательно, т может быть равно только 1,5, а значит, контейнер № 2 оказывается предназначен для цеха В;
– для k, таким образом, остается только 2, и контейнер № 3 оказывается предназначенным для цеха А.
15. Обозначая вес контейнера с товаром через х, а вес контейнера через у, можно математически записать условие задачи так:
х + (х + 2) = 8, откуда х = 3 тонны.
3 = y + 0,5 y, откуда у = 2 тонны.
Следовательно, вес товара равен: 3 - 2 = 1 тонна.
16. Да, это так. Парное число получается путем деления первого числа (а) на (а - 1). Так, если первый партнер внес 3 млн, то второй должен внести

При этом сложение капитала даст  млн, как и его умножение:
млн, как и его умножение: 
17. Необходимо первую бочку ставить строго по центру площадки, а все остальные ставить симметрично от центра по отношению к каждой очередной бочке другого предприятия.
18. Рассмотрим два численных примера.
1) Если ребро малого ящика равно 1 м, то длина, которую занимает груз, равна 1 + 2 x 1 = 3 погонных метра, и стоимость перевозки, исходя из длины груза, составляет 20 х 3 = 60 у. д. ед. При этом объем груза равен 13 +(2 x 1)3 =9м3, и стоимость перевозки, исходя из объема, составляет 20 х 9 = 180 у. д. ед. Следовательно, оплата с погонного метра значительно (в три раза) выгоднее.
2) Если ребро малого ящика равно 0,5 м, то длина, которую занимает груз, равна 0,5 + 2 х 0,5 =1,5 погонных метра, и стоимость перевозки, исходя из длины груза, составляет 20 х 1,5 = 30 у. д. ед. При этом объем груза равен (0,5)3 +(2 x 0,5)3 =1,125м3, и стоимость перевозки, исходя из объема, составляет 20 х 1,125 = = 22,50 у. д. ед. Следовательно, оплата здесь существенно выгоднее с объема (на 25 % дешевле).
Таким образом, ответ на вопрос задачи – какого вида оплата выгоднее – неоднозначен и зависит от размера груза.
Интересно и полезно узнать граничное значение этого размера – то, при котором оба вида оплаты равноценны.
Обозначим через х длину ребра малого ящика, при которой наступит равенство погонного и объемного размеров, учитываемых при оплате. При этом будет иметь место следующее очевидное равенство:
х + 2х х = х3 + (2 х х), или 3 x =9 x 3.

Итак, если ребро малого ящика короче 0,5 м, выгоднее платить исходя из объема, а если длиннее – исходя из длины. Проверим это утверждение.
При длине ребра малого ящика 0,58 м длина груза составит 0,58 + 2 х 0,58 = 1,74 погонных метра и стоимость перевозки будет равна 20 х 1,74 = 35 у. д. ед. При этом объем груза будет (0,58)3 +(2 x 0,58)3 = 1,74м3 и стоимость перевозки остается без изменений.
19. Первый шаг: поменять местами контейнеры 2 и 1. Второй шаг: поставить 5-й и 6-й после 7-го. Третий шаг: поставить 1-й и 3-й после 4-го. Четвертый шаг: 6-й и 8-й перенести в начало.
20. Обозначим количество приборов до прохождения ими контроля через х; количество приборов, оставшихся после прохождения 1-й ступени контроля, через х1, второй ступени контроля – х2 и т. д. При этом условие задачи можно математически записать следующим образом:

21. 1) Прежде всего найдем высоту прилегающего к шару цилиндра, равного шару по объему.
Объем шара равен  где R – радиус шара.
где R – радиус шара.
Объем прилегающего цилиндра, имеющего высоту, равную диаметру шара (так называемый описанный цилиндр), равен 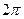 R 3.
R 3.
Отношение объема шара и цилиндра будет:
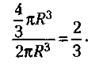
Следовательно, для того чтобы прилегающий к шару цилиндр имел объем, равный объему
2 шара, высота цилиндра должна составлять  от диаметра шара, т. е.
от диаметра шара, т. е.  м.
м.
2) Теперь задача сводится к нахождению суммарной длины того количества отрезков нити длиной по 0,4 м, которое укладывается в цилиндр с диаметром основания 0,6 м (как в пачке вермишели).
Площадь основания цилиндра равна:

Площадь сечения нити –  (0,1 мм)2. Количество отрезков нити, укладывающихся в наш цилиндр, равно:
(0,1 мм)2. Количество отрезков нити, укладывающихся в наш цилиндр, равно:

Длина нити равна суммарной длине этих отрезков, т. е. 9 х 106 х 0,4 м = 3 600 000 м, или 3600 км.
3) Количество катушек, необходимое, чтобы смотать эту нить, равно:

22. 1) Обозначим через х количество дней, за которое подразделение П1 смогло бы самостоятельно израсходовать весь складской запас, если бы он состоял только из цемента марки Б. При этом условие задачи можно записать так:

Откуда 140 + х = 5 х; х =  = 35 дней.
= 35 дней.
Поскольку фактически количество цемента Б на складе равно половине возможного запаса, подразделение П1 израсходует имеющийся цемент Б за половину срока:

2) Обозначим через у количество дней, за которое подразделение П2 смогло бы самостоятельно израсходовать весь складской запас, если бы он состоял только из цемента марки А. При этом:

Откуда 210 + 2у = 7у; у = 42 дня.
А фактически – половина этого запаса – за 21 день.
Но поскольку подразделения берут цемент совместно, то подразделение П2 к моменту, когда подразделение П1 выберет весь свой цемент Б, не успеет получить полностью свой цемент А. И то, что останется, они будут брать в дальнейшем сообща. Сколько же на это потребуется времени?
3) За те 17  дня, что подразделение П1 выберет весь цемент Б, подразделение П2 успеет выбрать
дня, что подразделение П1 выберет весь цемент Б, подразделение П2 успеет выбрать
17  : 42 =
: 42 =  всего складского запаса (если бы он состоял только из цемента А).
всего складского запаса (если бы он состоял только из цемента А).
Но так как фактически запас цемента А равен половине складского, то после истечения 17  дня на складе останется
дня на складе останется  всего складского запаса цемента А.
всего складского запаса цемента А.
Известно, что оба подразделения способны израсходовать весь складской запас цемента
марки А за 30 дней, следовательно, 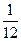 этого запаса за 30:
этого запаса за 30: 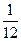 = 2
= 2  дня.
дня.
А всего оба подразделения выберут весь цемент за 17  + 2
+ 2  = 20 дней.
= 20 дней.
23. Обозначая через х и у возраст первого и последнего филиала соответственно, запишем условие задачи следующим образом:

Решая систему из двух уравнений с двумя неизвестными, получим:
х = 5у; 5у - у = 8,
откуда х = 2, у = 10.
24. Скорость судна при движении в реке по течению равна 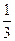 км/мин (20 км/ч). Скорость
км/мин (20 км/ч). Скорость
против течения -  км/мин (12 км/ч).
км/мин (12 км/ч).
1) Скорость судна при движении в море (без течения) равна средней скорости движения по течению и против него (то, что течение в одном случае добавляет, в другом отнимает):

25. Обозначим общее число работников через х, тогда условие задачи можно записать так:
количество электриков равно  ,
,
количество механиков  .
.
Откуда:
8 х 2(х - 1) + 3 х 3 (х - 1) = 8 х 3 х х; х = 25.
Количество электриков равно:

Количество механиков равно:

(включая головного сборщика).
26. Из второго условия задачи следует, что панели А и Б весят одинаково, а также что 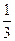 веса каждой из этих панелей равна 200 кг.
веса каждой из этих панелей равна 200 кг.
Следовательно, панели А и Б весят по 200 х 3 = 600 кг.
27. Обозначим через х стоимость обыкновенной акции. Тогда условие задачи можно записать так:

Решая уравнение, получим:

Всего по условию задачи 250 х 4 = 100 акций.
Из них обыкновенных 1000 - 250 = 750.
Следовательно, на 1 обыкновенную акцию предполагается выплатить

Количество привилегированных акций 250, следовательно, на 1 привилегированную акцию
предполагается выплатить 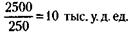
28. Обозначим через х общее количество стиральных машин четырех модификаций, собранных всеми двенадцатью предприятиями, и равные ему количества электронных и механических элементов, необходимых для их создания. Тогда количество электронных элементов четырех модификаций, необходимых для сборки машин на одном предприятии, будет равно  , а количество элементов одной модификации
, а количество элементов одной модификации  При этом количество этих элементов, производимых на каждом из трех электронных предприятий, должно быть равно,
При этом количество этих элементов, производимых на каждом из трех электронных предприятий, должно быть равно,

Интересующее нас минимальное количество этих элементов (xmin) будет иметь место при равенстве:


А на всех трех электронных предприятиях должно производиться 144 х 3 = 432 элемента каждой модификации, что дает возможность собрать 432 стиральные машины всех четырех модификаций. При этом на каждом предприятии будет производиться по 432: 12 = 36 стиральных машин всех четырех модификаций.
Проследим последовательность действий при кооперации предприятий от начала до конца:
– каждое из трех электронных предприятий производит 432: 3 = 144 электронных элемента четырех модификаций (36 х 4);
– каждое из девяти механических предприятий производит 432: 9 = 48 механических элементов;
– затем каждое электронное предприятие передает каждому механическому предприятию по 12 электронных элементов четырех модификаций (3 х 4), оставляя у себя 36 электронных элементов;
– а каждое механическое предприятие передает каждому электронному предприятию по 4 механических элемента, оставляя у себя 36 таких элементов;
– в результате на каждом из двенадцати электронных и механических предприятий оказывается по 36 электронных и по 36 механических элементов, из которых производится по 36 стиральных машин четырех модификаций.
Общее же количество стиральных машин равно 36 x 12 = 432.
29. Обозначим через хn общее количество производственных помещений, предназначенных для распределения очередной n -й паре, а через Н n и Ч n – количество помещений, выделенных предприятиям этой пары соответственно нечетных и четных номеров. Тогда по условиям задачи будут иметь место следующие очевидные соотношения:

По условиям задачи для последней пары

(так как каждой очередной паре достается равное количество ресурсов, а Н следующей пары на единицу больше, Ч должно быть на единицу меньше). Следовательно, из (2) следует:

По условиям задачи это равенство должно иметь место для любой пары, поэтому с учетом

а также

Поскольку для последней пары, где Чn = 0, Нn = 6 - 0 = 6, а для первой пары Н1 может быть минимально равно 0, при этом Ч1 = 6 - 0 = 6.
По условиям задачи от пары к паре количество производственных помещений для нечетных предприятий увеличивается на единицу, в распределении может участвовать всего 7 пар (имеющих Нn от 0 до 6, включая 0), т. е. 7 х 2 = = 14 малых предприятий. При этом в соответствии с (*):

Итак:
1) Ресурсы могут распределяться между 14 малыми предприятиями.
2) Всего распределяется 42 производственных помещения. Торговых точек для уравнивания возможностей МП должно быть столько, чтобы у каждого предприятия было по 6 единиц ресурсов, т. е. каждая пара предприятий должна получить по 6 торговых точек, а всего 6 x 7 пар предприятий = 42 торговые точки.
3) Количество ресурсов обоих видов, полученных каждым предприятием, будет следующим:

30. Оказывается, это довольно просто. Дело в том, что, к счастью аудитора, суммы цифр в обоих слагаемых оказались кратны 9, а значит – слагаемые делятся на 9. Естественно, делились на 9 они и до перестановки в них цифр. При сложении же чисел, делящихся на 9, сумма также делится на 9. Это означает, что сумма цифр результата сложения должна быть кратна 9. Сложив цифры суммы (кроме подделанной), получим 30. Ближайшее большее число, кратное 9, это 36. Нам не хватает 36 - 30 = 6. Следовательно, исправленная цифра – это 6.
31. Обозначим через х площадь арендуемого фирмой помещения, а через у – количество единиц продукции, идущих в уплату аренды. Тогда условие задачи можно записать так:

32. Обозначим через т, п, р, q количество контейнеров, поставляемых фирмами первой четверки (не обязательно в порядке последовательности фирм), которые являются партнерами соответствующих (в порядке номеров) фирм второй четверки (т - поставка партнера фирмы № 5, п - фирмы № 6 и т. д.). При этом условие задачи можно записать так:

(44 –это разность общего количества контейнеров и 20 – числа контейнеров, поставляемых первой четверкой: 2 + 4 + 6 + 8 = 20).

Умножая обе части (2) на 2, получим:

Из последнего выражения следует, что q может быть равно только 4, ибо по условиям задачи:
1) q, m,p должны быть целыми положительными числами,
2) эти числа различны и могут быть только 2, 4, 6, 8,
3) 2 не подходит, так как при этом т = р,
4) 6 и 8 не подходят, так как при этом т - р>8. Итак, q = 4.
Тогда из (*) следует, что 2(4-2) = m-р, т- р = 4.
Последняя разность может иметь место лишь при следующих значениях пары т и р:

Первая пара не подходит, так как число 4 уже имеет «хозяина» – ему равно q. Следовательно, т = 6р = 2.
Для п остается лишь значение, равное 8.

Если выстроить значение этих показателей по ранжиру (р, q, т, п), то эта последовательность и будет соответствовать последовательности номеров фирм-партнеров из второй четверки фирмам первой четверки (где была последовательность т, п, р, q):
фирма № 5 является партнером фирмы № 3,
фирма № 6 является партнером фирмы № 4,
фирма № 7 является партнером фирмы № 1,
фирма № 8 является партнером фирмы № 2.
Подставляя соответствующие значения в (1), нетрудно рассчитать количество контейнеров, поставляемых фирмами второй четверки.
Итоговые данные по поставкам всеми фирмами будут следующими:

33. Обозначим начальные фонды, равные у обоих предприятий, через х. Тогда к моменту окончания первой операции предприятие А обладало фондом в размере, равном х + 30, а предприятие Б – х - 30 тыс. у. д. ед. К моменту окончания второй операции фонд предприятия А составлял:

34. Взнос предпринимателя В, равный 320 тыс. у. д. ед., составляет  прежнего складского капитала. Значит, весь этот капитал был равен 320 х 3 = 960 тыс. у. д. ед. Причем в этом капитале доли А и Б относились как 1,5: 1, т. е. были соответственно равны 576 и 384 тыс. у. д. ед.
прежнего складского капитала. Значит, весь этот капитал был равен 320 х 3 = 960 тыс. у. д. ед. Причем в этом капитале доли А и Б относились как 1,5: 1, т. е. были соответственно равны 576 и 384 тыс. у. д. ед.
Теперь нужно разделить сумму, равную взносу В, между А и Б так, чтобы у каждого из них оказалось по  от нового складского капитала, который будет так же, как и старый, равен 960 тыс. у. д. ед. (взнос В не войдет в этот капитал, так как будет роздан А и Б). Для этого нужно вернуть предпринимателю А столько денег, чтобы его доля после этого оказалась равной 960: 3 = 320 у. д. ед. Иными словами, он должен получить 576 - 320 = 256 тыс. у. д. ед. Предприниматель Б должен получить 384 - 320 = 64 тыс. у. д. ед.
от нового складского капитала, который будет так же, как и старый, равен 960 тыс. у. д. ед. (взнос В не войдет в этот капитал, так как будет роздан А и Б). Для этого нужно вернуть предпринимателю А столько денег, чтобы его доля после этого оказалась равной 960: 3 = 320 у. д. ед. Иными словами, он должен получить 576 - 320 = 256 тыс. у. д. ед. Предприниматель Б должен получить 384 - 320 = 64 тыс. у. д. ед.
35. Обозначим через длину отрезка проволоки, причитающейся владельцу Б. Тогда условие задачи можно будет записать так:

Решая это уравнение, получим:
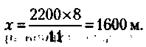
Владельцу А будет причитаться:

36. Обозначим через х стоимость месячного содержания помещений. Тогда условие задачи можно записать так:

Откуда, после преобразований, х = 150 тыс. у. д. ед.
Вычитая полученную стоимость содержания помещений из дохода, получим величину ежемесячных потерь арендатора:

37. Обозначим через х количество участков для субаренды. Тогда выручка за субаренду составит 8х, годовой заработок будет равен

и условие задачи запишется так:

После преобразований получим:

Решая квадратное уравнение по стандартной формуле, получим:

Следовательно:
1) Количество участков равно 12.
2) Прибыль арендатора равна:

38. Обозначим через Ст, Ср и Мл обобщенных представителей старших, средних и младших владельцев каждой группы. Тогда по условиям задачи:
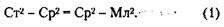
Это равнозначно следующим обозначениям:

так как, подставляя значения из (2) в (1), получаем тождество:

Далее, вводя новые обозначения, можно показать, что имеют место следующие равенства:
 (3)
(3)
так как, подставляя значения из (3) в (2), получаем тождество:

Обозначим

Тогда с учетом (2) и (3) можно записать:

Подбираем значения m и n исходя из следующих условий:
– т > п (иначе z будет отрицательным или равным 0, что противоречит условиям задачи);
– т и п должны быть целыми положительными числами разной четности (разная четность т и n объясняется так: 1) из Ср2 = х2 + у2 следует разная четность х и у – сторон прямоугольного треугольника; 2) поскольку у = 2ху в любом случае четен, х должен быть нечетным; 3) чтобы х был нечетным, необходимо, чтобы тип,связанные с х зависимостью х = т2 - п2, были разной четности);
– т и п должны удовлетворять условию х1 + у1 = Ср2 (из х2 + у2 должен без остатка извлекаться квадратный корень):

Наименьшей возможной парой т и п, удовлетворяющей всем этим условиям, является пара 8 и 7. При этом

Поскольку по условиям задачи минимальная доля (2 тыс. у. д. ед.) принадлежит младшему афганцу, ему причитается и наименьшая премия, равная 2'2 = 4 тыс. у. д. ед. Откуда премия среднего афганца равна:

а старшего афганца –

Соответственно их доли составляют:

Доля средней сестры равна:

а ее премия –

Премия младшей сестры равна:
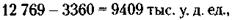
а старшей–
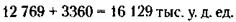
Соответственно их доли составляют:
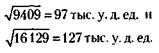
Доля старшего брата равна:
127 - 33 = 94 тыс. у. д. ед.,
а его премия – 942 = 8836 тыс. у. д. ед.
Премия среднего брата равна:
8836 - 3360 = 5476 тыс. у. д. ед,
а младшего брата –
5476 - 3360 = 2116 тыс. у. д. ед.
Соответственно их доли составляют:

39. Обозначим общее количество отечественных и иностранных фирм через х (при этом х должен быть целым, положительным и четным числом). Тогда каждая фирма должна израсходовать

При этом х может быть 2, 4, 6...
С учетом того, что конструкция А стоит 1 тыс. у. д. ед., конструкция Б –  а конструкция В –
а конструкция В –  будем рассуждать так:
будем рассуждать так:
х = 2 отпадает, так как речь идет о ряде как отечественных, так и иностранных фирм;
х = 4 также не проходит, так как при этом каждая фирма способна тратить  тыс. у. д. ед. и не может на эти деньги купить целое число конструкций всех видов;
тыс. у. д. ед. и не может на эти деньги купить целое число конструкций всех видов;
при х = 6 расходы каждой фирмы составили  На эти деньги можно купить по одной конструкции вида А, по одной конструкции вида Б и по одной – вида В:
На эти деньги можно купить по одной конструкции вида А, по одной конструкции вида Б и по одной – вида В:

Это и будет ответом на первый вопрос.
Общее количество фирм, участвующих в покупке, равно 6 (3 отечественные и 3 иностранные).
40. Обозначая момент проверки постов охраны через х1 можно математически записать условие задачи так:

Решая это уравнение, получим:

41. Вероятность получения счастливого билета (Р) может быть определена по следующей формуле из теории вероятностей:

Этот расчет можно проверить, собрав достаточное количество (порядка тысячи) любых билетов с шестизначными номерами и сосчитав, сколько счастливых приходится в среднем на сотню. Должно получиться 5–6 билетов.
42. 1) Обозначим через О, М и Д возраст отца, матери и дочери в момент заключения страхового договора. При этом условие задачи математически запишется так:

в момент заключения договора,

в момент заключения договора,

в момент выплаты страховой премии (через М лет).
Из (2) следует, что О = 12Д.
Подставляя значение О в (3), получим:
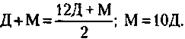
Подставляя значение О и М в (1), получим: 12Д + 10Д + Д = 46, откуда Д - 2 года, О = 12Д = 24 года, М = 10Д = 20 лет.
2) Страховая премия должна быть выплачена через М = 20 лет после заключения договора.
43. Обозначим через х первоначальное количество работников в каждом малом предприятии, а через у – первоначальное количество этих предприятий. Тогда количество предприятий после первой реорганизации будет у -10, а количество работников в каждом из них х + 1. После второй реорганизации получим соответственно у – 10 - 15 = у - 25 предприятий и х+ 1 + 2 = х + 3работника в каждом.
При данном условии задачи можно записать так:

Из (1) следует:

Совместно решая (1) и (2), получим:

Подставляя (*) в (**), получим:


Общая численность работников объединения равна:

44. Обозначим время от полудня до противостояния стрелок через х, а число делений, проходимых часовой стрелкой от цифры 12 до момента противостояния, – через у. Тогда условие задачи можно записать следующим образом:
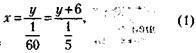
где  – скорость минутной, а
– скорость минутной, а  – скорость часовой стрелки.
– скорость часовой стрелки.

1) Следовательно, заседание должно начаться в 12 ч 32 мин 43,6 с.
2) Следующее противостояние должно произойти через 2х часов, т. е. через
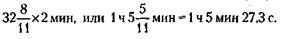
45. Проанализируем ситуацию с помощью графика (см. рис.).
По оси х откладывается время возможного прихода партнера А, а по оси у – партнера Б. Тогда время, в течение которого они могут встретиться, будет соответствовать заштрихованному участку графика. Действительно, если партнер А придет на встречу в начале срока (точка 0), то его встреча с партнером Б состоится, лишь если Б придет на встречу в пределах от 0 до 20 мин от начала срока. Если он придет позже, встреча не состоится, так как А уже уйдет. Если же А придет на встречу на 40-й мин, то он встретится с Б, лишь если тот придет между 20-й и 60-й мин. И так для всех точек заштрихованной области.

Вероятность встречи может быть найдена как отношение шансов, благоприятствующих встрече (заштрихованная область), ко всем возможным шансам (площадь квадрата со стороной в 60 мин). При этом, как видно из рисунка, площадь, соответствующая всем возможным шансам, равна:

а площадь, соответствующая благоприятным шансам, равна разности полученной площади и двух треугольников:

Следовательно, искомая вероятность встречи равна:

Иными словами, встреча состоится 5–6 раз из 10.
46. Обозначим новые оклады работников начальными буквами соответствующих специальностей. Тогда условие задачи можно будет записать так:

Группируя оклады, получим:

Поскольку Р + М = 2500, выражение (*) можно представить так:

откуда

И далее:

1) Учитывая, что эти оклады составляют 100 - 25 = 75 % от соответствующих окладов до сокращения, несложно рассчитать, чему были равны тогда упомянутые оклады (пометим их штрихами):

Расходы на зарплату составляли удвоенную сумму этих окладов:

2) Следовательно, экономия средств, полученная предприятием за счет сокращения, равна:
14400-11 300 = 3100 у. д. ед. в месяц.
47. Обозначив через х количество персонала на предприятии до реорганизации, а через у – количество дней, на которые хватает при этом зарплаты, запишем условие задачи следующим образом:

Решая это уравнение относительно второго и третьего равенств, получим:
180 у = 15 х - 600,
откуда

Из (*) следует также, что
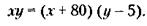
Подставляя в последнее выражение значение у, получим:

откуда х = 400 человек, у = 30 дней.
Следовательно:
1) В настоящее время на предприятии работает 400 человек.
2) Величина месячной (30-дневной) зарплаты составляет:

48. Вначале определим количество участков, на которые увеличится садоводство:

Обозначим через х сторону садоводства до его увеличения, выраженную в длинах сторон участков. Тогда площадь садоводства до увеличения составит х2, а после увеличения (x + n)2, где п = 1, 2, 3, 4, 5... (целые числа натурального ряда, соответствующие приросту длины садоводства, выраженной в длинах сторон участков). Теперь условие задачи можно записать так:

Откуда


Анализ последнего выражения и условий задачи показывает, что x2 и п должны быть целыми числами, а п, кроме того, должно быть нечетным (иначе 161 не разделится на него без остатка) и на него должно делится без остатка 161. Этим условиям из первых 10 цифр натурального ряда отвечают только 1 и 7. Но 7 не подходит, так как в этом случае х = 7 = п и из выражения (*) следует, что
 – не целое число.
– не целое число.
Итак, п = 1. Это означает, что
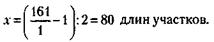
Следовательно:
1) Количество участков в садоводстве до его увеличения было

а после увеличения:

или, что то же самое, 6400 + 161 = 6561 участок.
2) Сторона садоводства при увеличении должна вырасти на длину одного участка (n = 1), т. е. на

3) Площадь садоводства до увеличения была равна:

а после увеличения:
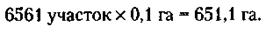
49. Обозначим через х количество работников, а через у – их зарплату при работе предприятия в нормальном режиме. Тогда условие задачи можно записать так:

Из второго равенства уравнения (*) следует:

Из первого равенства уравнения (*) следует:

Подставляя в последнее выражение значение х, получим:


Итак:
1) Численность персонала при работе в нормальном режиме составляет 40 человек; зарплата при этом равна 9 тыс. у. д. ед.
2) Фонд заработной платы равен 40 х 9 = 360 тыс. у. д. ед.
3) Численность персонала при работе в период спада равна 40 - 10 = 30 человек, а зарплата 9 + 3 = 12 тыс. у. д. ед.; численность персонала при работе в период увеличения загрузки равна 40 + 50 = 90 человек, а зарплата 9-5 = 4 тыс. у. д. ед.
50. 1) Исходя из того, что 6 путевок в Каркодайл равноценны 9 путевкам в Фингалию, определим относительную ценность этих путевок.
Она составит 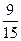 для Каркодайла и
для Каркодайла и  для Фингалии.
для Фингалии.
2) Исходя из этих относительных стоимостей и зная, что поездка в Каркодайл и в Фингалию в сумме оценивается в 90 банок икры, рассчитаем стоимость каждой из путевок в отдельности:
путевка в Каркодайл стоит 
путевка в Фингалию
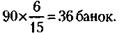
3) Информация о двух возможных вариантах приобретаемого количества путевок позволяет составить систему из двух уравнений с двумя неизвестными:

где К и Ф – количество путевок в Каркодайл и Фингалию соответственно.
Решение этой системы уравнений позволяет найти К = 7 и Ф = 9.
4) Подставляя эти цифры в уравнение, соответствующее второму варианту сделки, можно получить искомое количество банок икры, выделенных для этой сделки:

51. 1) В исходном положении сосуд № 1 содержит 1,1л тоника, а сосуд № 2 – 0,5 л джина.
2) Из сосуда № 1 в сосуд № 2 переливается 0,5 л тоника (чтобы удвоить там количество жидкости). Теперь в сосуде № 1 осталось 0,6 л тоника, а в сосуде № 2 оказался 1 л смеси, состоящей поровну из джина и тоника.
3) Из сосуда № 2 в сосуд № 1 переливается 0,6 л (столько, сколько оставалось в сосуде № 1) смеси, состоящей из 0,3 л джина и 0,3 л тоника. Теперь в сосуде № 1 0,3 л джина и 0,9 л тоника, а в сосуде № 2 осталось 0,2 л джина и 0,2 л тоника.
4) Из сосуда № 1 в сосуд № 2 переливается 0,4 л (чтобы удвоить там количество) смеси, содержащей 0,1 л джина и 0,3 л тоника (смесь в сосуде № 1 имеет соотношение джина и тоника 1: 3).
После всего этого количество жидкости в сосудах становится по 0,8 л.
В сосуде № 1 образовалась смесь из 0,6 л джина и 0,2 л тоника (3: 1 – крепкий коктейль).
В сосуде № 2 – смесь из 0,3 л джина и 0,5 л тоника (3: 5 – слабый коктейль).
52. Используя формулу сложных процентов для приведения взносов к моменту покупки (см. задачу 150), получим:

41,7 тыс. у. д. ед. – это и есть действительная стоимость дома на момент покупки.
Следовательно, покупатель, назвав сумму 40 тыс. у. д. ед., предложил весьма выгодную для себя сделку.
53. Обозначив количество голосов, поданных за различные виды пасты, их начальными буквами, можно представить результаты маркетингового исследования в таком виде:
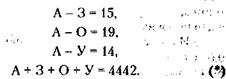
Суммируя первые три выражения, получим:

Складывая (*) и (**), получим:
4А = 4500, откуда А = 1125 голосов.
Соответственно:

54. 1) Общая прибыль от операции купли-продажи квартир составляет 14% - 11 % = 3 %. Следовательно, цена покупки обеих квартир равна 500 тыс. у. д. ед. (3 % от 500 = 15, т. е. 515-500).
2) Обозначая цену покупки 1-й квартиры через х, а 2-й квартиры через у, можно записать условие задачи следующим образом:

Решим систему из двух уравнений с двумя неизвестными.

откуда

Цена продажи 1-й квартиры 280 х (1+0,14) = 280 х 1,14 = 319,2 тыс. у. д. ед.
Цена продажи 2-й квартиры 220 х (1-0,11) = 220 х 0,89 = 195,8 тыс. у. д. ед.
55. Обозначив через х количество оплаченных компьютеров (без премии), через у – стоимость каждого оплаченного компьютера, а через у – количество премиальных компьютеров, можно представить условие задачи следующим образом:

Решим полученную систему из трех уравнений с тремя неизвестными:

Подставляя значение у в (2), получим:

Подставляя значение х в (3), получим:


Итак, 1) без учета премии было приобретено 16 компьютеров по цене 750 у. д. ед.; 2) в виде премии было получено 2 компьютера.
56. Обозначив через х количество первоначально оплаченных дубленок, а через у – цену дубленки без учета стимулирования, можно записать условие задачи следующим образом:

Поиск по сайту: