Необходимое условие экстремума)

Если функция 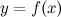имеет экстремум в точке 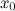, то ее производная 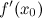либо равна нулю, либо не существует.

(Первое достаточное условие экстремума)

Пусть для функции 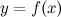выполнены следующие условия:

1. функция непрерывна в окрестности точки ;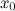

2. 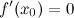или 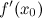не существует;

3. производная 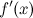при переходе через точку 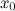меняет свой знак.

Тогда в точке 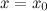функция 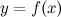имеет экстремум, причем это минимум, если при переходе через точку 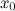производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку 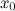производная меняет свой знак с плюса на минус.

25.

(Второе достаточное условие экстремума)

Пусть для функции 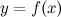выполнены следующие условия:

1. она непрерывна в окрестности точки ;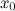

2. первая производная 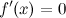в точке ;

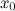3. в точке .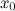

Тогда в точке 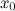достигается экстремум, причем, если 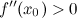, то в точке 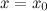функция 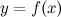имеет минимум; если , то в точке 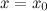функция 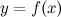достигает максимум.

26.

(Об условиях выпуклости или вогнутости графика функции)

Пусть функция 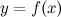определена на интервале 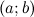и имеет непрерывную, не равную нулю в точке 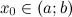вторую производную. Тогда, если 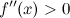всюду на интервале 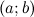, то функция имеет вогнутость на этом интервале, если 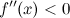, то функция имеет выпуклость.

27.

Точкой перегиба графика функции 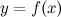называется точка 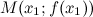, разделяющая промежутки выпуклости и вогнутости.

28.

Прямая 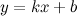называется наклонной асимптотой графика функции 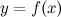, если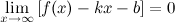

(условиях существования наклонной асимптоты)

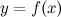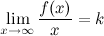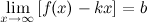Если для функции существуют пределы и , то функция имеет наклонную асимптоту 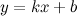при .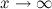

29.

1. Область определения и область допустимых значений функции.

2. Четность, нечетность функции.

3. Точки пересечения с осями.

4. Асимптоты функции.

5. Экстремумы и интервалы монотонности.

6. Точки перегиба и промежутки выпуклости, вогнутости.

7. Сводная таблица.

30.

Определение. Кривизной 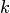дуги кривой 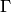в данной точке 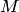называется предел средней кривизны дуги 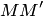, когда длина этой дуги стремится к нулю:

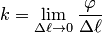
Поиск по сайту: