Определение производной

Рассмотрим функцию f(x), область определения которой содержит некоторый открытый интервал вокруг точки x ₀. Тогда функция f(x) является дифференцируемой в точке x ₀, и ее производная определяется формулой

Для производной используются обозначения:

Для нахождения производной функции f(x) в точке x ₀ на основе определения следует выполнить следующие действия:

• Записать отношение ;
• Упростить дробь, сократив ее, если возможно, на Δ x;
• Найти производную 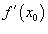, вычисляя предел дроби. Если данный предел существует, то говорят, что функция f(x) дифференцируема в точке x = x ₀.

В примерах ниже мы выведем производные основных элементарных функций, используя приведенное формальное определение производной. Эти функции составляют основной костяк в том смысле, что производные других функций можно выразить уже через них, применяя правила действий с производными.

17.

18.

U'*V+V'*U - Производная суммы

U'*V-V'*U _ Производная разности

V²

19.

Дифференциалом функции в называется главная, линейная относительно , часть приращения функции.

.

Покажем, что и эквивалентные бесконечно малые при :

( - бесконечно малая).

Геометрический смысл дифференциала:

П роведем к графику функции в точку касательную 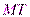и рассмотрим ординату этой касательной для точки . На рисунке , . Из прямоугольного треугольника имеем: , т.е. . Но, согласно геометрическому смыслу производной, . Поэтому 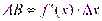или . Это означает, что дифференциал функции в равен приращению ординаты касательной к графику функции в этой точке, когда получает приращение .

^1.

^2.

^3.

^4.

^5.

^6.

^7.

^8.

^9.

^10.

^11.

^12.

^13.

^14.

^15.

^16.

^17.

^18.

^19.

^20.

Теоремы Роля, Лагранжа, Коши.

Теорема Ферма. (О равенстве нулю производной)

Пусть функция 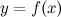удовлетворяет следующим условиям:

1. она дифференцируема на интервале ;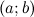

2. достигает наибольшего или наименьшего значения в точке .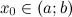

Тогда производная в этой точке равна нулю, то есть .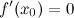

Теорема Ролля. (О нуле производной функции, принимающей на концах отрезка равные значения)

Пусть функция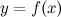

1. непрерывна на отрезке ;

2. дифференцируема на интервале ;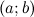

3. на концах отрезка принимает равные значения .

Тогда на интервале 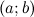найдется, по крайней мере, одна точка 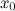, в которой .

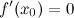Теорема Лагранжа. (О конечных приращениях)

Пусть функция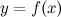

1. непрерывна на отрезке ;

2. дифференцируема на интервале .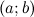

Тогда на интервале 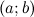найдется по крайней мере одна точка 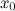, такая, что

21.

(Правило Лопиталя).

Пусть функци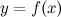и и удовлетворяют следующим условиям:

1) эти функции дифференцируемы в окрестности точки , кроме, может быть, самой точки ;

2) и в этой окрестности;

3) ;

4) 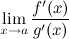существует конечный или бесконечный.

Тогда существует и , причем

22.

Поиск по сайту: