История

Домашняя работа

(В конце слайдов: придумать свой шарж или стишок про Пифагора)

Цель: продолжить воспитание у школьников устойчивого интереса к предмету

Развивать смекалку и наблюдательность.

Воспитывать познавательный интерес к предмету, любовь к поисковым решениям.

(На доске шаржи на Пифагора) Из-за иллюстрирующих теорему чертежей ее называли "ветряной мельницей", рисовали забавные карикатуры, придумывали шутливые стишки в виде такого

Пифагоровы штаны

на все стороны равны..

А носил ли Пифагор сам те штаны,

Которые на все стороны равны?

История

Цель: Познакомить учащихся с историческим материалом

Мы уже говорили, что теорема Пифагора применялась для решения различных задач еще задолго до Пифагора древними египтянами, индусами и другими древними народами. Ценным источником математических знаний Древней Индии является книга "Правила веревки". Значительную часть книги занимает правило построения прямого угла.

Землемеры Древнего Египта для построения прямого угла использовали бечевку, разделенную на 12 частей. Покажите, как это они делали.

Натягивателей веревок называли гарпедонаптами.

Исторические задачи:

Цель задач: Совершенствовать навыки решения задач на применение теоремы Пифагора и теоремы

Показать применение этих теорем в решении исторических задач

1) Задача индийского математика Бхаскары (Задача, записанная в стихотворной форме роздана учащимся), на проекторе иллюстрация к задаче.

На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. Угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Оказалось три фута всего от ствола.
Прошу тебя, мне поскорее скажи:
У тополя как велика высота?
Бхаскара "Венец системы" 1150 г.

2.1) Задача древних индусов

Над озером тихим, с полфута размером,
Высится лотоса цвет.
Он рос одиноко. И ветер порывом
Отнес его в сторону. Нет
Больше цветка над водой.
Нашел же рыбак его ранней весной
В двух футах от места, где рос.
И так, предложу я вопрос;
Как озера вода здесь глубока?

Решение.

АС = х, АВ = х + , АВ² = АС² + СВ²,

, АС = 4 – , АС = (фута).

2.2) Аналогичная (видоизмененая задача более ложного уровня)

Верхняя часть тростника, растущего в реке, выступает над поверхностью воды. Как определить глубину реки, производя измерения только на поверхности или над поверхностью реки?

Пусть над поверхностью воды выступает часть тростника ^ ВС = а и пусть искомая глу­бина реки АВ равна х.Взяв за конец С тростника, наклоним его в положение AD так, чтобы верхняя его точка С косну­лась воды. Расстояние BD = b можно измерить, расстояние AD = АС = АВ + ВС = х + а. Из прямоугольного треугольника АВD имеем:

AD² = BD² + AB² или (х + а)² = b² + x², откуда х = (b² – а²): 2а

3)Арабская задача про птиц

На разных берегах реки растет по пальме. Высота одной – 30 локтей, другой 20, а расстояние между основаниями пальм – 50 локтей. На верхушке каждой пальмы сидит птица. Обе птицы заметили птицу, всплывшую на поверхность реки между пальмами. Птицы кинулись разом и достигли ее одновременно. На каком расстоянии от более высокой башни всплыла рыба?

4)Задача Леонардо Пизанского

XIII век. Две башни в равнине находятся на расстоянии 60 локтей одна от другой. Высота первой башни 50 локтей, высота второй 40 локтей. Между башнями находится колодец, одинаково удаленный от вершин башен. Как далеко находится колодец от основания каждой башни

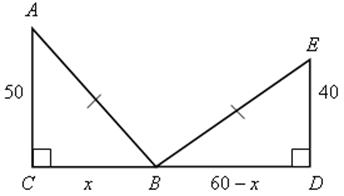
АСВ, 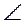С = 90°,

АВ2 = АС2 + СВ2;

ВЕD, 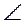D = 90°,

ВЕ2 = ВD2 + ЕD2.

Так как АВ2 = ВЕ2, то 502 + х2 = (60 – х)2 + 402

х = 22,5.

СВ = 22,5; ВD = 37,5.

Ответ: 23 и 38 локтей.

Поиск по сайту: