Задачи с практическим применением

Цель

Совершенствовать навыки решения задач на применение теоремы Пифагора и теоремы, обратной теореме Пифагора.

Показать практическое применение этих теорем.

1. Задача кассирши Эльнары

Три монеты лежат на столе, ка­саясь друг друга, а их центры образуют прямоуголь­ный треугольник. Приведите их размеры, выражен­ные наименьшими возможными целыми числами. (На решение задачи дается 1 мин. Карандашом и бумагой пользоваться нельзя.)

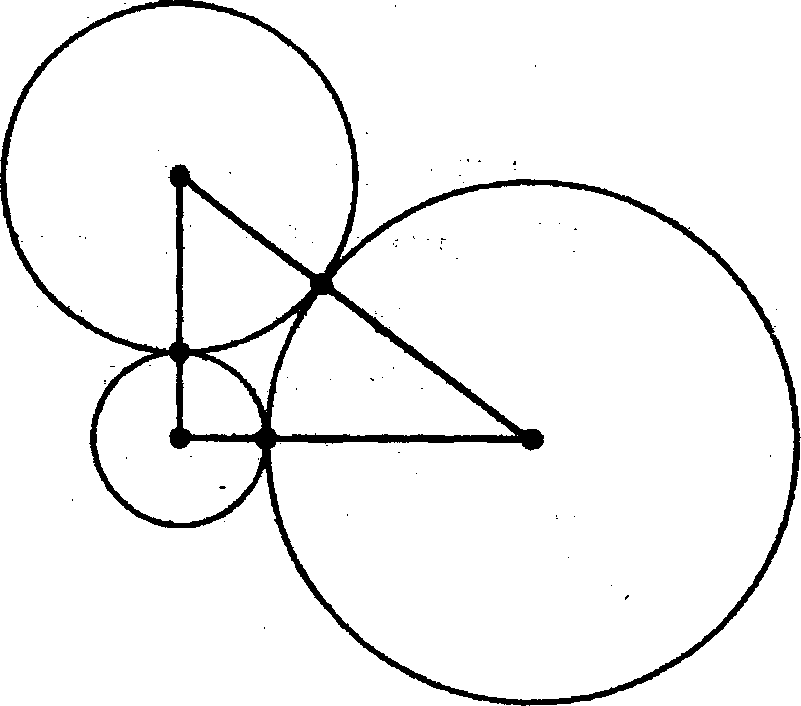
2. Из "Арифметики" Магницкого (самостоятельно)

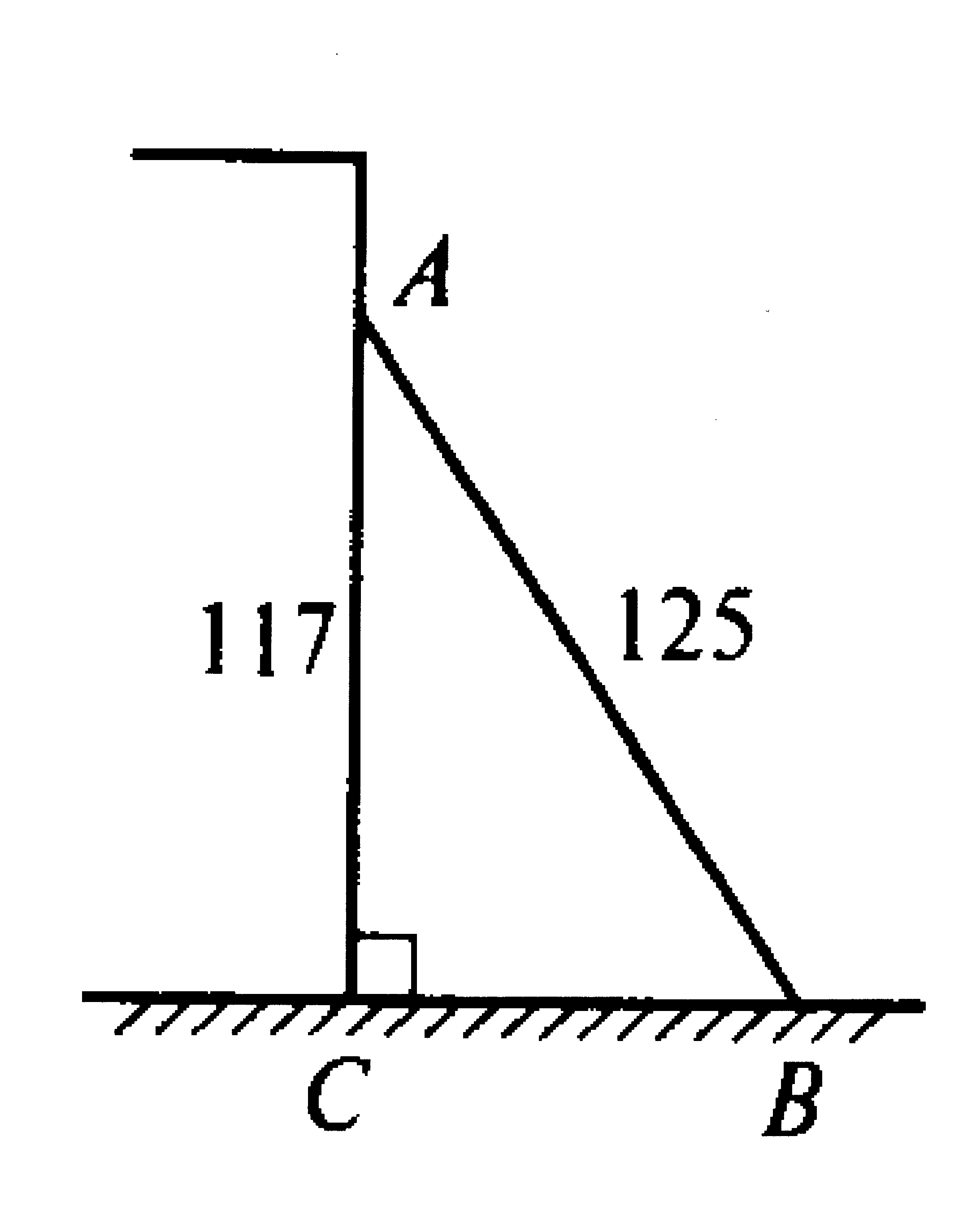Случися некоему человеку к сте­не лествицу прибрати, стены же тоя высота есть 117 стоп. И обрете лествицу долготою 125 стоп. И ведати хощет, колико стоп сея лествицы нижний ко­нец от стены отстояти имать.

3. Путь жука.

У дороги лежит тесаный гранитный камень в 30 см дли­ны, 20 см высоты и такой же толщины. В точке А — жук, намеревающийся кратчайшим путем направиться к углу В. Как пролегает этот кратчайший путь и какой он длины?

Решение:

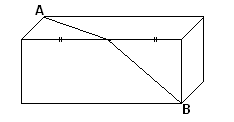
Кратчайший путь легко определится, если мы мысленно повернем верхнюю грань камня так, чтобы она оказалась в одной плоскости с передней. Тогда АВ – кратчайший путь. АВ = 50 см.

4. Путешествие шмеля

Шмель отправляется в дальнее путешествие. Из родного гнезда он летит прямо на юг, пересекает речку и наконец после целого часа пути спускается на косогор, покрытый душистым клевером. Здесь, перелетая с цветка на цветок, шмель остается полчаса.

Теперь надо посетить сад, где шмель вчера заметил цве­тущие кусты крыжовника. Сад лежит на запад от косогора, и шмель спешит прямо туда. Спустя 3/4 часа он был уже в саду. Крыжовник в полном цвету, и, чтобы посетить все кусты, понадобилось шмелю 1 /2 часа. А затем, не отвле­каясь в стороны, шмель кратчайшей дорогой полетел до­мой, в родное гнездо.

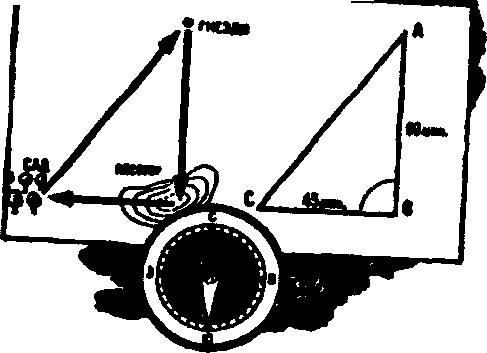Найдем, сколько времени понадобилось шмелю на перелет из сада в гнездо. Начертим путь шмеля. Мы знаем, что шмель летел сначала прямо на юг в течении 60 минут. Затем он летел 45 минут на запад, т.е. под прямым углом к прежнему пути. Оттуда кратчайшей дорогой, т.е. по прямой линии, обратно к гнезду. Треугольник АВС - прямоугольный. АС = 75 мин = 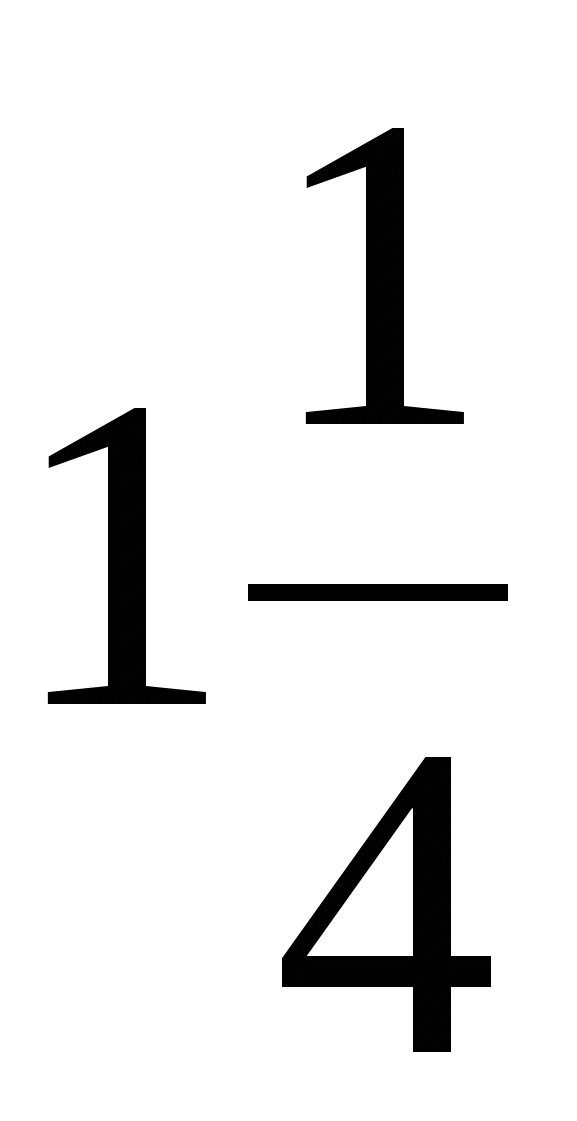ч.

Ответ: 5 ч. Пробыл шмель в отсутствии.

5.Про эскалатор

Эскалатор метрополитена имеет 17 ступенек от пола наземного вестибюля до пола подземной станции. Ширина ступенек 40 см, высота 20 см. Определите а) длину лестницы, б) глубину станции по вертикали.

Решение.

а) Пусть АВ – длина лестницы из 17 ступенек. Из 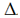АКD по теореме Пифагора АD = 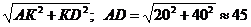(см), АВ = 45 • 17 = 765 (см) = 7, 65 (м). б) ВС = 40 • 17 = 680 (см). Из АСВ по теореме Пифагора АС = 3,5 (м).

Ответ: длина лестницы 7, 65 м, глубина станции 3,5 м.

6.Про пловца

Пловец поплыл от берега реки, всё время гребя в направлении по перпендикуляру к берегу (берега реки считаем параллельными). Плыл он, приближаясь к противоположному берегу со скоростью 3 км/ч. Через 5 мин. он был на противоположном берегу. Узнайте, на каком расстоянии от мести начала заплыва он вышел на противоположном берегу, считая скорость течения всюду равной 6 км/ч.

Ответ: 560 м.

ГОТИКА

Поиск по сайту: