Энергия взаимодействия системы точечных зарядов. Энергия заряженного проводника

1) Электростатические силы взаимо­действия консервативны, следовательно, система зарядов обладает потенци­альной энергией.

Найдем потенциальную энергию системы двух неподвижных точеч­ных зарядов Q ₁и Q ₂, находящихся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией:

(32)

где j ₁₂ и j ₂₁ — соответственно потенциалы, создаваемые зарядом Q ₂ в точке нахожде­ния заряда Q ₁ и зарядом Q ₁ в точке нахождения заряда Q ₂.

(33)

поэтому W ₁ = W ₂ = W и

(34)

Добавляя к системе из двух зарядов последовательно заряды Q ₃, Q ₄ ,..., можно убедиться в том, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна

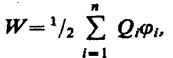(35)

где j_i — потенциал, создаваемый в той точке, где находится заряд Q_i, всеми зарядами, кроме i -го.

2) Пусть имеется уединенный провод­ник, заряд, емкость и потенциал которого соответственно равны: Q, С, j. Увеличим заряд этого проводника на d Q. Для этого необходимо перенести заряд d Q из бесконеч­ности на уединенный проводник, затратив на это работу, равную

(36)

Чтобы зарядить тело от нулевого потенциала до j, необходимо совершить работу

(37)

Энергия заряженного проводника равна той работе, которую необходимо совер­шить, чтобы зарядить этот проводник:

(38)

Потенциал проводника во всех его точках одинаков, так как поверхность проводника является эквипотенциальной. Пола­гая потенциал проводника равным j, найдем:

(39)

где - заряд проводника.

26. Энергия заряженного конденсатора. Как всякий заряженный проводник, конден­сатор обладает энергией, которая в соответствии с формулой (95.3) равна

(40)

где Q — заряд конденсатора, С — его емкость, Dj — разность потенциалов между обкладками конденсатора.

27. Объемная плотность энергии электростатического поля. Преобразуем формулу (40), выражающую энергию плоского конденсатора посредством зарядов и потенциалов и воспользовав­шись выражением для емкости плоского конденсатора (C=e ₀ eS/d) и разности потенци­алов между его обкладками (D j = Ed), получим:

(41)

где V= Sd — объем конденсатора. Формула (41) показывает, что энергия конден­сатора выражается через величину, характеризующую электростатическое поле, — на­пряженность Е.

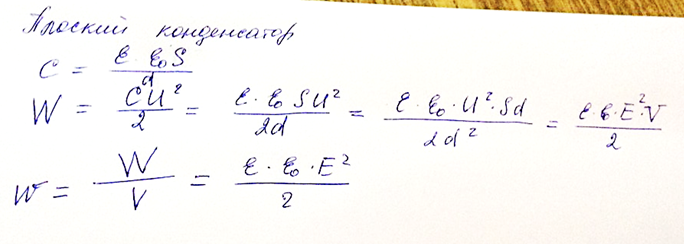Объемная плотность энергии электростатического поля (энергия единицы объема)

(42)

Формулы (40) и (42) соответственно связывают энергию конденсатора с зарядом на его обкладках и с напряженностью поля.

28.

29.

· сила тока I (служит количественной мерой электрического тока)- скалярная физи­ческая величина, определяемая электрическим зарядом, проходящим через поперечное сечение проводника в единицу времени:

· плотность тока — физическая величина, определяемая силой тока, проходящего через единицу площа­ди поперечного сечения проводника, перпендикулярного направлению тока

— вектор, ориентированный по направлению тока (т.е. направление вектора j совпадает с направлением упорядоченного движения положительных зарядов.

Единица плотности тока — ампер на метр в квадрате (А/м²).

Сила тока сквозь произвольную поверхность S определяется как поток вектора j, т. е.

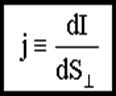
· Выражение для плотности тока через среднюю скорость носителей тока и их концентрацию

За время dt через площадку dS пройдут заряды, отстоящие от нее не дальше чем на vdt (выражение для расстояния между зарядами и площадкой через скорость)

Заряд dq, прошедший за dt через dS

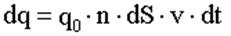
где q₀ - заряд одного носителя; n - число зарядов в единице объема (т.е их

концентрация): dS·v·dt - объем.

отсюда, выражение для плотности тока через среднюю скорость носителей тока и их концентрациюимеет следующий вид:

30.

· постоянный ток – ток, сила и направление которого не изменяются со времени.

где q — электрический заряд, проходящий за время t через поперечное сечение провод­ника. Единила силы тока — ампер (А).

· сторонние силы и ЭДС источника тока

сторонние силы -силы неэлектростатического происхождения, действующие на заряды со стороны источников тока.

Сторонние силы совершают работу по перемещению электрических зарядов.

Эти силы имеют электромагнитную природу: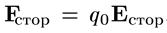

и их работа по переносу пробного заряда q пропорциональна q:

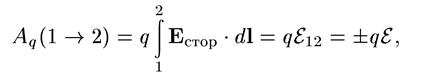
· Физи­ческая величина, определяемая работой, совершаемой сторонними силами при переме­щении единичного положительного заряда, называется электродвижущей силой (э.д.с.), действующей в цепи:

где е называют электродвижущей силой источника тока. Знак «+» соответствует случаю, когда при движении источник проходит в направлении действия сторонних сил (от отрицательной обкладки к положительной), «-» - противоположному случаю

31.

· Закон Ома для участка цепи

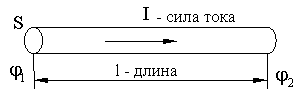
· Электрическое сопротивление

R – сопротивление проводника.

Единица сопротивления – Ом.

Для однородного проводника длиной l и сечением S:

ρ - удельное сопротивление

· Закон Ома для замкнутой цепи

Если электрическая цепь замкнута, то выбранные точки 1 и 2 со­впадают, j ₁= j ₂; тогда получаем закон Ома для замкнутой цепи:

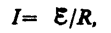
32.

· Закон Ома в локальной форме

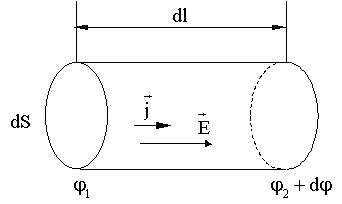
Закон Ома для элементарного объема проводника.

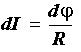
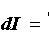
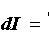
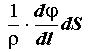
Обозначим величину, обратную плотности, где 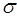- удельная проводимость.

Получим закон Ома в дифференциальной форме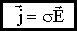

· Удельное сопротивление (см. пункт 31)

Закон Джоуля - Ленца в дифференциальной форме

Рисунок 6

Количество тепла, выделяемое в элементарном объеме с сопротивлением R при прохождении тока I в течение времени dt:

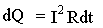- закон Джоуля - Ленца.

Найдем плотность мощности:

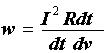
Количество теплоты, выделяющееся за единицу времени в единице объема, называется удельной тепловой мощностью тока.

Она равна

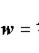
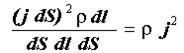
Закон Джоуля - Ленца в дифференциальной форме.

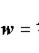
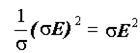
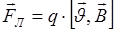Сила, действующая на электрический заряд, движущийся в магнитном поле со скоростью, называется силой Лоренца и выражается формулой

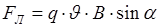Вращающий момент сил, можно определить с.о.:

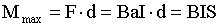
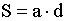
Вращающий момент сил зависит как от свойств поля в данной точке, так и от свойств рамки и определяется формулой

,

где 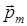— вектор магнитного момента рамки с током ( 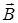— вектор магнитной индукции, количественная характеристика магнитного поля). Для плоского контура с током I

где S — площадь поверхности контура (рамки) ,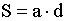

n — единичный вектор нормали к по­верхности рамки.

Магнитная индукция в данной точке однородного магнитного поля определяется максимальным вращающим моментом, действующим на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна направлению поля.

[B] – Тл (Тесла).

Магнитное поле является силовым, следовательно, его можно изображать, с помощью линий магнитной индукции — линий, касательные к которым в каждой точке совпадают с направлением вектора В.

Свойства линий магнитной индукции:

 замкнуты, т.к. в природе нет магнитных зарядов;

 вектор В направлен по касательной к линии магнитной индукции;

 густота линий магнитной индукции пропорциональна модулю вектора В.

Движение заряженных частиц в магнитном поле

Выражение для силы Лоренца позволяет найти ряд закономерностей движения заряженных частиц в магнитном поле. Направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле зависят от знака заряда частицы. На этом основано определение знака заряда частиц, движущихся в магнитных полях.

Для вывода общих закономерностей будем считать, что магнитное поле однородно и на частицы электрические поля не действуют. Если заряженная частица движется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол a между векторами v и В равен 0 или p. Тогда по формуле (32) сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно.

Вектор скорости параллелен вектору магнитной индукции (рис.9)

Рисунок 9

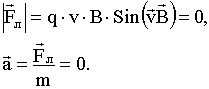
Частица движется равномерно и прямолинейно, вдоль магнитного поля.

Если заряженная частица движется в магнитном поле со скоростью v, перпен­дикулярной вектору В, то сила Лоренца постоянна по модулю и нормальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центро­стремительное ускорение. Отсюда следует, что частица будет двигаться по окружности (рис.2).

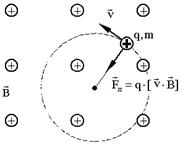
Рисунок 2

Линии индукции направлены за чертеж, В = const. Ускорение

нормальное ускорение.

Частица движется по окружности такого радиуса:

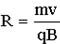
Время одного полного оборота:

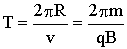
т. е. период вращения частицы в однородном магнитном поле определяется только величиной, обратной удельному заряду (q/m) частицы, и магнитной индукцией поля, но не зависит от ее скорости (при v<<c). На этом основано действие циклических ускорителей заряженных частиц.

Если скорость v заряженной частицы направлена под углом a к вектору В (рис. 1), то ее движение можно представить в виде суперпозиции: 1) равномерного прямолиней­ного движения вдоль поля со скоростью v _|| =v cos a; 2) равномерного движения со скоростью v _^= v sin a по окружности в плоскости, перпендикулярной полю.

плоскости, перпендикулярной полю.

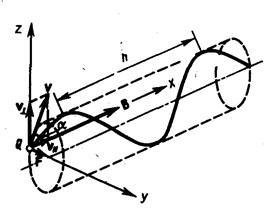
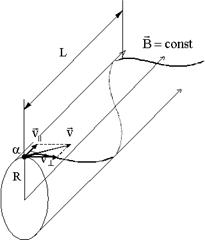
Рис. 1

Радиус окружности определяется формулой (34) (в данном случае надо заменить v на v _^= v sin a). В результате сложения обоих движений возникает движение по спирали, ось которой параллельна магнитному полю (рис. 1). Шаг винтовой линии

Подставив в последнее выражение (35), получим

Направление, в котором закручивается спираль, зависит от знака заряда частицы.

Если скорость заряженной частицы составляет угол a с направлением векто­ра В неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, то r и h уменьшаются с ростом В. На этом основана фокусировка заряженных частиц в магнитном поле.

37.

Поиск по сайту: