Электронный механизм ЭДС индукции

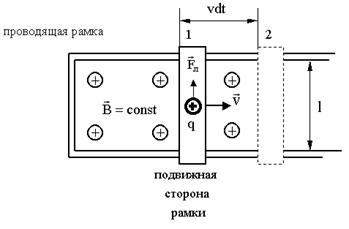
Рисунок 2

На рисунке 2 изображена рамка с подвижной стороной. Магнитное поле направлено от нас. Тянем подвижную сторону со скоростью 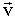. На заряд +q действует сила Лоренца

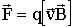
Перемещающая заряд на расстояние l и совершающая работу

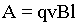
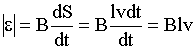
Результат тот же, значит: электронный механизм возникновения ЭДС индукции - это работа компоненты силы Лоренца.

Таким образом, возбуждение э.д.с. индукции при движения контура в постоянном магнитном поле объясняется действием силы Лоренца, возникающей при движении проводника.

54.

Электрический ток, текущий в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, по закону Био — Савара — Лапласа, пропорциональ­на току. Сцепленный с контуром магнитный поток Ф поэтому пропорционален току I в контуре:

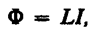(6)

где коэффициент пропорциональности L называется индуктивностью контура.

При изменении силы тока в контуре будет изменяться также и сцепленный с ним магнитный поток; следовательно, в контуре будет индуцироваться э.д.с.

Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией.

Единица индуктивности генри (Гн): 1 Гн — ин­дуктивность такого контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб:

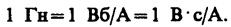
Индуктивность контура в общем случае зависит только от геометрической формы контура, его размеров и магнитной проницаемости той среды, в которой он находится.

Применяя к явлению самоиндукции закон Фарадея, получим, что э. д.с. самоиндукции

Если контур не деформируется и магнитная проницаемость среды не изменяется (в дальнейшем будет показано, что последнее условие выполняется не всегда), то L = const и

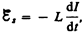(10)

где знак минус, обусловленный правилом Ленца, показывает, что наличие индуктив­ности в контуре приводит к замедлению изменения тока в нем.

Если ток со временем возрастает, то 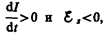т. е. ток самоиндукции направлен навстречу току, обусловленному внешним источником, и замедляет его возрастание.

Если ток со временем убывает, то т. е. индукционный ток имеет такое же направление, как и убывающий ток в контуре, и замедляет его убывание.

Таким образом, контур, обладая определенной индуктивностью, приобрета­ет электрическую инертность, заключающуюся в том, что любое изменение тока тормозится тем сильнее, чем больше индуктивность контура.

55*. Рассчитаем индуктивность бесконечно длинного соленоида (рис.4).

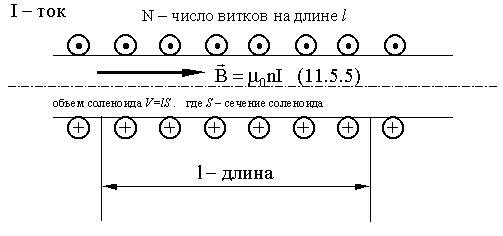
Рисунок 4

Магнитная индукция однородного поля внутри соленоида с сердечником с магнитной проницае­мостью m, равна

Магнитный поток сквозь один виток соленоида площадью S равен

а полный магнитный поток, сцепленный со всеми витками соленоида и называемый потокосцеплением,

(7)

Согласно (7), полный магнитный поток сквозь соленоид (потокосцепление) равен

Подставив это выражение в формулу (6), получим

(8)

т. е. индуктивность соленоида зависит от числа витков соленоида N, его длины l, площади S и магнитной проницаемости m вещества, из которого изготовлен сердечник соленоида.

Обозначим через

число витков на единицу длины

Тогда формулу (8) можно будет переписать в виде:

(9)

56.

Магни́тная инду́кция — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд 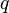, движущийся со скоростью .

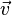Более конкретно, — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля^[1] на заряд 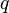, движущийся со скоростью, равна

, где α угол меду векторами и .

Напряжённость магни́тного по́ля (стандартное обозначение Н) — векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M.

В Международной системе единиц (СИ): где — магнитная постоянная.

Для количественного описания намагничения магнетиков вводят векторную величину — намагниченность, определяемую магнитным моментом единицы объема магнетика:

где — магнитный момент магнетика, представляющий собой векторную сумму магнитных моментов отдельных молекул.

Связь между J и напряженностью магнитного поля H в диамагнитных и парамагнитныхматериалах, обычно линейна (по крайней мере, при не слишком больших величинах намагничивающего поля):

где χ _m называют магнитной восприимчивостью. В ферромагнитных материалах нет однозначной связи между J и H из-за магнитного гистерезиса и чтобы описать зависимость используют тензор магнитной восприимчивости.

Магнитная индукция определяется через намагниченность как:

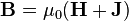
57. Магнитная проницаемость и магнитная восприимчивость. Их определения и связь между ними.

Магнитная восприимчивость — физическая величина, характеризующая связь между магнитным моментом (намагниченностью) вещества и магнитным полем в этом веществе.

Магнитная проницаемость — физическая величина, коэффициент (зависящий от свойств среды), характеризующий связь между магнитной индукцией {B} и напряжённостью магнитного поля {H} в веществе.

Магнитная проницаемость связана с магнитной восприимчивостью χ следующим образом:

в СИ:

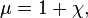
в Гауссовой системе:

58. Циркуляция вектора напряженности магнитного поля.

Теорема о циркуляции магнитного поля.

Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции.

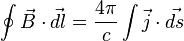
Здесь B — вектор магнитной индукции, j — плотность тока; интегрирование слева производится по произвольному замкнутому контуру, справа — по произвольной поверхности, натянутой на этот контур.

Поиск по сайту: